Проанализируем решение задачи, используя условия дополняющей нежесткости (вторую теорему двойственности)

Прямая задача имеет оптимальное решение, вычислим оптимальное решение двойственной задачи, используя условия дополняющей нежесткости Решим симплекс-методом задачу линейного программирования, используя метод искусственного базиса Проанализируем решение задачи, используя условия дополняющей нежесткости (вторую теорему двойственности) Метод Фогеля Метод потенциалов Венгерский метод

38492

знака

таблиц

изображений

Решим симплекс-методом задачу линейного программирования, используя метод искусственного базиса Читать далее: Метод Фогеля

5. Проанализируем решение задачи, используя условия дополняющей нежесткости (вторую теорему двойственности).

Подставляем координаты оптимального решения двойственной задачи в систему ограничений.

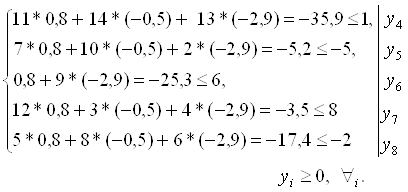
Первое, третье и пятое ограничения выполняются как строгие неравенства, следовательно, их координаты оптимального решения исходной задачи равны нулю: . Учитывая это, первую, вторую и пятую координаты оптимального решения Х^* находим при совместном решении уравнений-ограничений исходной задачи:

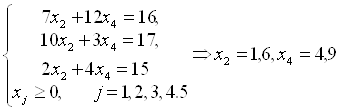
Ответ: Z(X) = 4,2 при Х* = (0;1,6; 0;4,9;0).

Задача № 3

Транспортная задача

Ниже приведены числовые данные транспортных задач. Стоимость перевозки единицы продукции записаны в клетках таблицы. Запасы указаны справа от таблиц, а потребности – снизу. Требуется построить начальный план методами: «северо-западного угла», «минимального элемента», «двойного предпочтения», методом Фогеля. Из каждого плана найти оптимальный план методом потенциалов.

	24
34	30	39	29	18	82
40	35	45	41	10	36
36	38	41	50	8	79
14	10	13	10	12	80
77	60	22	68	50

Решение.

1.Метод северо-западного угла.

Исходные данные задачи сведем в таблицу (табл. 3.1).

Таблица 3.1.

Поставщики	Потребители					Запасы
Поставщики						Запасы
	34	30	39	29	18	82
	40	35	45	41	10	36
	36	38	41	50	8	79
	14	10	13	10	12	80
Потребности	77	60	22	68	50

Решение. Построим опорный план задачи методом северо-западного угла.

Объем перевозки и последовательность заполнения матрицы будем записывать в соответствующие клетки табл. 3.2.

Цифры, стоящие в скобках над объемами перевозок, обозначают номер шага, на котором определяются эти перевозки.

1. х₁₁⁽¹⁾=min(82,77)=77. Потребности первого потребителя удовлетворены, исключаем его. Запасы первого поставщика уменьшились на х₁₁⁽¹⁾и стали равны (82-77=5) 5.

2. х₁₂⁽¹⁾=min(5,60)=5. Запасы первого поставщика исчерпаны, исключим первую строку. Второй потребитель удовлетворил свои потребности на 5 единиц, его спрос уменьшился на величину х₁₁⁽¹⁾ и стал равным 55.

3. х₂₂⁽³⁾=min(36,55)=36. После третьего шага ресурсы поставщика А₂исчерпаны. Спрос потребителя B₂ равен b₂⁽³⁾=55-36=19.

4. х₂₃⁽⁴⁾=min(79,19)=19. Следует исключить потребителя B_2. Ресурсы поставщика А₃⁽⁴⁾ = a₃ – х₂₃⁽⁴⁾=79-19=60 составляет 60 единиц.

5. х₃₃⁽⁵⁾=min(60,22)=22. Потребитель В₃ полностью удовлетворил свой спрос, исключаем столбец 3.

6. х₃₄⁽⁶⁾=min(38,68)=38. Следует исключить поставщика А₃, запасы которого исчерпаны. Спрос потребителя В₄ в₄⁽⁶⁾ – х₃₄⁽⁵⁾=68-38=30 составляет 30 единиц.

7. х₄₄⁽⁷⁾=min(80,30)=30. Спрос четвертого потребителя удовлетворен. Запасы поставщика А₄составляет

80-30=50.

8. х₄₅⁽⁸⁾=min(50,50)=0. Запасы исчерпаны, потребности удовлетворены.

Опорный план построен (табл. 3.2).

Таблица 3.2.

34	30	39	29	18
77⁽¹⁾	5⁽²⁾				82
40	35	45	41	10
	36⁽³⁾				36
36	38	41	50	8
	19⁽⁴⁾	22⁽⁵⁾	38⁽⁶⁾		79
14	10	13	10	12
			30⁽⁷⁾	50⁽⁸⁾	80
77	60	22	68	50

Суммарные транспортные издержки на перевозку продукции от поставщиков к потребителю составляют

2.Метод минимального элемента.

Исходные данные

поставщики	потребители					Запасы
поставщики	В₁	В₂	В₃	В₄	В₅	Запасы
А₁	34	30	39	29	18	82
А₂	40	35	45	41	10	36
А₃	36	38	41	50	8	79
А₄	14	10	13	10	12	80
потребности	77	60	22	68	50

1. Объем запасов и потребностей после первого шага уменьшается на величину: х₃₁⁽¹⁾=50; . Запасы пятого поставщика исчерпаны, потребности первого потребителя уменьшились на 50 единиц и стали равны 29, исключаем пятый столбец.

2. . Объем запасов и потребностей после второго шага уменьшается на величину: х₄₂⁽²⁾=60; . Потребности пункта В₂ удовлетворены, исключим из рассмотрения второй столбец.

3. . Объем запасов и потребностей после третьего шага уменьшается на величину: х₄₄⁽³⁾=20; . Запасы пункта А₄ исчерпаны, исключим из рассмотрения четвертую строку.

4. . Корректируем объемы запасов и потребностей после четвертого шага: . Потребности пункта В₄ удовлетворены, исключим четвертый столбец.

5. . После пятого шага запасы поставщика А₁ будут исчерпаны, исключаем первую строку. Потребности В₁равны: .

6. . После шестого шага запасы третьего поставщика будут исчерпаны , потребности первого потребителя равны . Исключаем третью строку.

7. . После седьмого шага запасы второго поставщика будут равны , потребности первого потребителя удовлетворены.

8. . После восьмого шага запасы и потребности будут удовлетворены.

Потребности всех потребителей удовлетворены, запасы поставщиков исчерпаны. После седьмого шага мы получили исходный опорный план (Табл.3.3).

Х₀Таблица 3.3.

34	30	39	29	18
34⁽⁵⁾			48⁽⁴⁾		82
40	35	45	41	10
14⁽⁷⁾		22⁽⁸⁾			36
36	38	41	50	8
29⁽⁶⁾				50⁽¹⁾	79
14	10	13	10	12
	60⁽²⁾		20⁽³⁾		80

77	60	22	68	50

Также как и в предыдущем случае, номер шага помещен в скобках над объемами перевозок. Суммарные транспортные расходы, соответствующие данному плану перевозок равны

По сравнению с расчетом по методу северо-западного угла суммарные транспортные расходы уменьшились с 8452 у.е. до 6342 у.е.

Для проверки плана на оптимальность составим систему уравнений, следуя условию — для базисных переменных сумма потенциалов равна тарифу. Значение одного из потенциалов зададим произвольно (пусть ), последовательность вычисления остальных потенциалов указана ниже: 1), 2),…, 8).

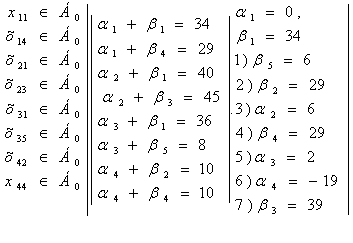
Потенциалы поставщиков поместим слева от таблицы, а потенциалы потребителей – сверху над таблицей (табл.3.4).

Таблица 3.4

		34		29		39		29			6
0	34		30		39		29		18
		34⁽⁵⁾						48⁽⁴⁾				82
			-1		0					-12
6	40		35		45		41		10
		14⁽⁷⁾				22⁽⁸⁾						36
			0				-6		-2
2	36		38		41		50		8
		29⁽⁶⁾									50⁽¹⁾	79
			-7		0		-19
-19	14		10		13		10		12
				60⁽²⁾				20⁽³⁾				80
	1				7				-25
		77		60		22		68			50

Для небазисных переменных вычислим оценки по формуле:

Значения оценок поместим в левом нижнем углу незанятых клеток табл. 3.4. Фиксируем наибольшую положительную оценку. В данном случае: . Разрешающей объявим коммуникацию (4,3). Строим цикл пересчета, который показан в табл. 3.4 пунктирной линией.

Величина корректировки ρ=(58,79)=58. Вносим изменение в план: перевозки отрицательного полуцикла уменьшаем на , а перевозки положительного полуцикла увеличиваем на эту же величину, остальные перевозки оставим без изменения. Переменная х₁₁вводится в базис со значением =58,переменная х₁₄выводится из базиса. Получим план (табл. 3.5).

План Таблица 3.5

		34		29		39		29			6
0	34		30		39		29		18
		34⁽⁵⁾						48⁽⁴⁾				82
			-1		0					-12
6	40		35		45		41		10
		14⁽⁷⁾				22						36
			0				-6		-2
2	36		38		41		50		8
		29⁽⁶⁾									50⁽¹⁾	79
			-7		0		-19
-19	14		10		13		10		12
				60⁽²⁾				20⁽³⁾				80
	1				7				-25
		77		60		22		68			50

Значение функции уменьшилось на (38*16-9*38=290) и стало:

План не оптимален. Заново вычисляем потенциалы и оценки (табл. 3.6). Наибольшая положительная оценка– это , план не оптимален. Строим цикл пересчета и определяем величину корректировки плана ρ=(48,58)=48.

Таблица 3.6

План X₂

		34		29		39		29			6
0	34		30		39		29		18
				14				68⁽⁴⁾				82
			-1		0					-12
6	40		35		45		41		10
											36	36
			0				-6		-2
2	36		38		41		50		8
		65									14	79
			-7		0		-19
-19	14		10		13		10		12
		12		46⁽²⁾		22						80
	1				7				-25
		77		60		22		68			50

Значение функции и соответственно транспортные расходы составили

Положительных оценок нет, план Х₂оптимален.

Раздел: Экономико-математическое моделирование
Количество знаков с пробелами: 38492
Количество таблиц: 36
Количество изображений: 26

Скачать

... Ю.Н. Математические методы в экономике: Учебник.2-е изд. – М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. – 368 с. 7. Монахов А.В. Математические методы анализа экономики. – Спб: Питер, 2002. – 176 с. 8. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов /В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др., Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. ...

Скачать

... того чтобы получить оптимальное решение нужно перейти на лист «Расчет» через основное меню, нажав кнопку «Расчеты». На листе «Расчет» представлена математическая модель оптимизации распределения трудовых ресурсов (рис 3.3) описанная в разделе 3.2. Данная модель использует надстройку «Поиск решений» MS Excel Рис 3.3. Для запуска надстройки «Поиск решений» MS Excel, необходимо в главном меню ...

Скачать

... продукции. Кроме того, т.к. объем ресурсов для оборудования дается в часах, а производительность оборудования в м¤/час, то необходимо перейти к соизмеримости. Таким образом, задача сводится к нахождению оптимального плана производства продукции каждого вида с целью получения максимальной прибыли. ЗЛП будет выглядеть так: Целевая функция: min Z = 0.51x1+0.57x2+0.13x3+0.33x4+0.38x5+0.72x6+0.23x7+0. ...

Скачать

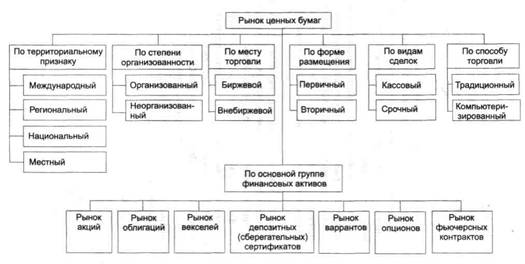
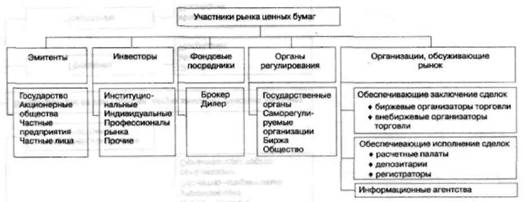
... важной составной частью как денежного рынка, так и рынка капиталов, которые в совокупности составляют финансовый рынок. Цель функционирования рынка ценных бумаг -как и всех финансовых рынков - состоит в том, чтобы обеспечивать наличие механизма для привлечения инвестиций в экономику путем установления необходимых контактов между теми, кто нуждается в средствах, и теми, кто хотел бы инвестировать ...

Главная Новости Рефераты Статьи Вузы

О проекте Соглашение

Наверх

Войти на сайт

Навигация

Похожие работы

0 комментариев

Разделы

Инфо

Следите за новостями