Навигация
Венгерский метод
2. Венгерский метод.
Предварительный этап. Исходная матрица C:
| 31 | 13 | 11 | 41 | 10 | 17 | 38 | 25 |
| 35 | 20 | 26 | 8 | 17 | 14 | 38 | 36 |
| 12 | 37 | 38 | 49 | 38 | 22 | 10 | 13 |
| 28 | 21 | 48 | 43 | 44 | 29 | 26 | 12 |
| 37 | 22 | 39 | 46 | 26 | 20 | 44 | 49 |
| 22 | 49 | 19 | 2 | 20 | 30 | 45 | 16 |
| 45 | 27 | 5 | 21 | 30 | 21 | 34 | 23 |
| 43 | 33 | 20 | 29 | 3 | 46 | 33 | 21 |
Шаг 1. Обозначим через ![]() наибольший элемент столбца
наибольший элемент столбца ![]() матрицы
матрицы ![]() (r1=45, r2=49, r3=48, r4=49, r5=44, r6=46, r7=45, r8=49). Каждый элемент
(r1=45, r2=49, r3=48, r4=49, r5=44, r6=46, r7=45, r8=49). Каждый элемент ![]() -го столбца вычтем из
-го столбца вычтем из ![]() , результаты вычислений будем помещать на место вычитаемого. Аналогичные преобразования проводим в остальных столбцах. Получим неотрицательную матрицу
, результаты вычислений будем помещать на место вычитаемого. Аналогичные преобразования проводим в остальных столбцах. Получим неотрицательную матрицу ![]() , в каждом столбце которой есть хотя бы один нуль.
, в каждом столбце которой есть хотя бы один нуль.
| C1 = | 14 | 36 | 37 | 8 | 34 | 29 | 7 | 24 |
| 10 | 29 | 22 | 41 | 27 | 32 | 7 | 13 | |
| 33 | 12 | 10 | 0 | 6 | 24 | 35 | 36 | |
| 17 | 28 | 0 | 6 | 0 | 17 | 19 | 37 | |
| 8 | 27 | 9 | 3 | 18 | 26 | 1 | 0 | |
| 23 | 0 | 29 | 47 | 24 | 16 | 0 | 30 | |
| 0 | 22 | 43 | 28 | 14 | 25 | 11 | 23 | |
| 2 | 16 | 28 | 20 | 41 | 0 | 12 | 25 |
Шаг 2. Преобразуем матрицу ![]() . Для этого обозначим через
. Для этого обозначим через ![]() минимальный элемент строки
минимальный элемент строки ![]() , который последовательно вычтем из элементов той же строки, результаты поместим на место уменьшаемого. Наименьший элемент первой строки матрицы
, который последовательно вычтем из элементов той же строки, результаты поместим на место уменьшаемого. Наименьший элемент первой строки матрицы ![]() равен 7. Проведем вычисления для элементов первой строки: (d11=7, d12=29, d13=30, d14=1, d15=27, d16=22, d17=0, d18=17). Такие же вычисления проведем для остальных строк, получим неотрицательную матрицу
равен 7. Проведем вычисления для элементов первой строки: (d11=7, d12=29, d13=30, d14=1, d15=27, d16=22, d17=0, d18=17). Такие же вычисления проведем для остальных строк, получим неотрицательную матрицу ![]() , в каждом столбце и каждой строке которой есть хотя бы один нуль.
, в каждом столбце и каждой строке которой есть хотя бы один нуль.
| D= | 7 | 29 | 30 | 1 | 27 | 22 | 0* | 17 |
| 3 | 22 | 15 | 34 | 20 | 25 | 0 | 6 | |
| 33 | 12 | 10 | 0* | 6 | 24 | 35 | 36 | |
| 17 | 28 | 0* | 6 | 0 | 17 | 19 | 37 | |
| 8 | 27 | 9 | 3 | 18 | 26 | 1 | 0* | |
| 23 | 0* | 29 | 47 | 24 | 16 | 0 | 30 | |
| 0* | 22 | 43 | 28 | 14 | 25 | 11 | 23 | |
| 2 | 16 | 28 | 20 | 41 | 0* | 12 | 25 |
Основной этап. После второго шага предварительного этапа получим неотрицательную матрицу ![]() , эквивалентную матрице эффективностей
, эквивалентную матрице эффективностей ![]() :
:
П.1. В первом столбце матрицы ![]() отметим звездочкой 0*7,1 ,во втором столбце – 06,2 , в третьем столбце – 04,3, в четвертом столбце – 0*3,4 , в шестом столбце – 08,6, в седьмом столбце – 01,7 , в восьмом столбце – 05,8. Нули в пятом столбце – 04,5 нельзя отметить звездочкой, так как они лежат в строке, в которой уже есть нуль со звездочкой – 04,3,. Число звездочек равно семи, что меньше размерности матрицы (8), переходим к п.2.
отметим звездочкой 0*7,1 ,во втором столбце – 06,2 , в третьем столбце – 04,3, в четвертом столбце – 0*3,4 , в шестом столбце – 08,6, в седьмом столбце – 01,7 , в восьмом столбце – 05,8. Нули в пятом столбце – 04,5 нельзя отметить звездочкой, так как они лежат в строке, в которой уже есть нуль со звездочкой – 04,3,. Число звездочек равно семи, что меньше размерности матрицы (8), переходим к п.2.
| D= | + | + | + | + | + | + | + | ||
| 7 | 29 | 30 | 1 | 27 | 22 | 0* | 17 | ||
| 3 | 22 | 15 | 34 | 20 | 25 | 0’ | 6 | ||
| 33 | 12 | 10 | 0* | 6 | 24 | 35 | 36 | ||
| 17 | 28 | 0* | 6 | 0’ | 17 | 19 | 37 | + | |
| 8 | 27 | 9 | 3 | 18 | 26 | 1 | 0* | ||
| 23 | 0* | 29 | 47 | 24 | 16 | 0’ | 30 | ||
| 0* | 22 | 43 | 28 | 14 | 25 | 11 | 23 | ||
| 2 | 16 | 28 | 20 | 41 | 0* | 12 | 25 |
![]() ε=2
ε=2
П.2. Помечаем знаком «+» сверху столбцы: 1, 2, 3, 4,6, 7,8 и считаем эти столбцы занятыми. Незанятый нуль находится в четвертой строке пятого столбца 04,5 , во второй строке и шестой строках седьмого столбца. Помечаем их штрихом 0'4,5 , 0'2,7 , 0'6,7. Переходим к пункту 3.
П.3. Столбец 3 считаем незанятым и знак «+» сверху снимаем (обводим в рамку), а четвертую строку объявляем занятой и помечаем знаком «+» справа. Возвращаемся к третьему абзацу п.2.
П.2. Незанятых нулей нет, переходим к п.5.
П.5. Среди незанятых элементов находим минимальный, который обозначим через ![]() , ε=d3,5=6. Преобразуем матрицу
, ε=d3,5=6. Преобразуем матрицу ![]() : незанятые элементы уменьшим на 6; дважды занятые увеличим на 6; остальные элементы оставим без изменения. Получим матрицу
: незанятые элементы уменьшим на 6; дважды занятые увеличим на 6; остальные элементы оставим без изменения. Получим матрицу ![]() , в которой имеется один незанятый нуль, переходим к четвертому абзацу п.2.
, в которой имеется один незанятый нуль, переходим к четвертому абзацу п.2.
| + | + | + | + | + | + | + | |||
| D1= | 7 | 29 | 24 | 1 | 21 | 22 | 0* | 17 | |
| 3 | 22 | 9 | 34 | 14 | 25 | 0’ | 6 | + | |
| 33 | 12 | 4 | 0* | 0’ | 24 | 35 | 36 | ||
| 23 | 34 | 0* | 12 | 0’ | 23 | 25 | 43 | + | |
| 8 | 27 | 3 | 3 | 12 | 26 | 1 | 0* | ||
| 23 | 0* | 23 | 47 | 18 | 16 | 0’ | 30 | ||
| 0* | 22 | 37 | 28 | 8 | 25 | 11 | 23 | ||
| 2 | 16 | 22 | 20 | 35 | 0* | 12 | 25 |
![]()
П.2. Незанятый нуль находится в третьей строке пятого столбца 03,5 . Помечаем штрихом 0'3,5. Во второй строке седьмого столбца находится нуль со штрихом. Помечаем штрихом 0'2,7 и считаем седьмой столбец незанятым, знак «+» сверху снимаем, а вторую строку объявляем занятой и помечаем знаком «+» справа.
| + | + | + | + | + | + | + | |||
| D2= | 7 | 29 | 24 | 1 | 21 | 22 | 0* | 17 | |
| 3 | 22 | 9 | 34 | 14 | 25 | 0’ | 6 | + | |
| 33 | 12 | 4 | 0* | 0’ | 24 | 35 | 36 | ||
| 23 | 34 | 0* | 12 | 0’ | 23 | 25 | 43 | + | |
| 8 | 27 | 3 | 3 | 12 | 26 | 1 | 0* | ||
| 23 | 0* | 23 | 47 | 18 | 16 | 0’ | 30 | ||
| 0* | 22 | 37 | 28 | 8 | 25 | 11 | 23 | ||
| 2 | 16 | 22 | 20 | 35 | 0* | 12 | 25 |
П.5. Переходим к пункту 2. Помечаем звездочкой 0*6,5, штрихом 0'8,3, 0'2,7. В третьей нет ![]() , следовательно, переходим к пункту 4, ε=d6,4=7 после преобразований, получим матрицу D3
, следовательно, переходим к пункту 4, ε=d6,4=7 после преобразований, получим матрицу D3
| + | + | + | + | + | + | + | |||
| D3= | 7 | 29 | 24 | 1 | 21 | 22 | 0* | 17 | |
| 3 | 22 | 9 | 34 | 14 | 25 | 0’ | 6 | + | |
| 33 | 12 | 4 | 0* | 0’ | 24 | 35 | 36 | ||
| 23 | 34 | 0* | 12 | 0’ | 23 | 25 | 43 | + | |
| 8 | 27 | 3 | 3 | 12 | 26 | 1 | 0* | ||
| 23 | 0* | 23 | 47 | 18 | 16 | 0’ | 30 | ||
| 0* | 22 | 37 | 28 | 8 | 25 | 11 | 23 | ||
| 2 | 16 | 22 | 20 | 35 | 0* | 12 | 25 |
![]()
П.4. Строим цепочку из нулей. Начиная от только что отмеченного штрихом нуля (0’2,7), идем по строке до ![]() 5,2 цепочка состоит из двух элементов Ц: 07,2, 0’5,2. В матрице такие цепочки обозначают так
5,2 цепочка состоит из двух элементов Ц: 07,2, 0’5,2. В матрице такие цепочки обозначают так ![]() . После преобразования получим новый набор нулей со звездочкой (
. После преобразования получим новый набор нулей со звездочкой (![]() ), который содержит на одну звездочку больше, чем предыдущий набор.
), который содержит на одну звездочку больше, чем предыдущий набор.
Проводим следующие пересчеты.
| + |
| + | + | + | + | ||||
| D3= | 25 | 0 | 0* | 27 | 19 | 16 | 20 | 32 | + |
| 3 | 43 | 2 | 7 | 23 | 14 | 5 | 0* | + | |
| 6 | 32 | 0 | 23 | 20 | 5 | 18 | 7 | + | |
| 0* | 36 | 10 |
| 0 | 5 | 2 | 17 | ||
|
|
| 9 | 19 | 5 | 45 | 19 | 12 | + | |
| 15 | 24 | 10 | 7 |
| 0* | 5 | 5 | ||
| 22 | 0* | 13 | 8 | 9 | 15 | 22 | 9 | ||
| 6 | 32 | 0 | 20 | 7 | 34 | 0* | 8 | + |
Процесс окончен, так как число нулей со звездочкой равно размерности матрицы эффективности.
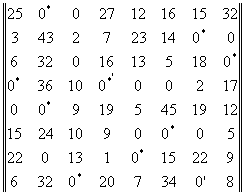
Оптимальный вариант выбора (1,2)(2,7)(3,8)(4,1)(5,4),(6,6),(7,5),(8,3). Это значит, что первая невеста выберет второго жениха, вторая невеста седьмого жениха, третья –восьмого, четвертая первого, пятая четвертого, шестая – шестого, седьмая невеста пятого жениха, а восьмая невеста выберет третьего жениха.
При этом максимальная суммарная эффективность (суммарная продолжительность жизни всех семей) равна: ![]() (единиц эффективности)
(единиц эффективности)
Похожие работы
... Ю.Н. Математические методы в экономике: Учебник.2-е изд. – М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. – 368 с. 7. Монахов А.В. Математические методы анализа экономики. – Спб: Питер, 2002. – 176 с. 8. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов /В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др., Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. ...
... того чтобы получить оптимальное решение нужно перейти на лист «Расчет» через основное меню, нажав кнопку «Расчеты». На листе «Расчет» представлена математическая модель оптимизации распределения трудовых ресурсов (рис 3.3) описанная в разделе 3.2. Данная модель использует надстройку «Поиск решений» MS Excel Рис 3.3. Для запуска надстройки «Поиск решений» MS Excel, необходимо в главном меню ...
... продукции. Кроме того, т.к. объем ресурсов для оборудования дается в часах, а производительность оборудования в м¤/час, то необходимо перейти к соизмеримости. Таким образом, задача сводится к нахождению оптимального плана производства продукции каждого вида с целью получения максимальной прибыли. ЗЛП будет выглядеть так: Целевая функция: min Z = 0.51x1+0.57x2+0.13x3+0.33x4+0.38x5+0.72x6+0.23x7+0. ...
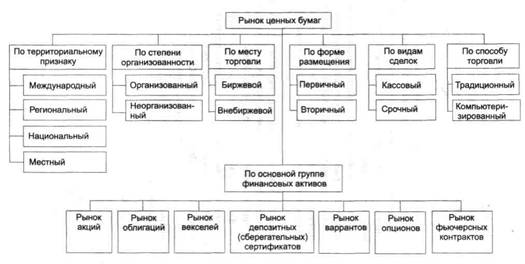
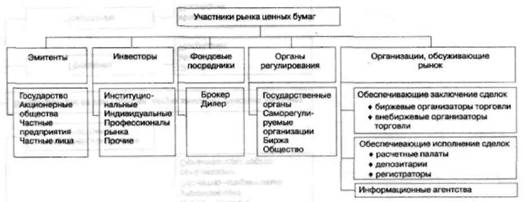
... важной составной частью как денежного рынка, так и рынка капиталов, которые в совокупности составляют финансовый рынок. Цель функционирования рынка ценных бумаг -как и всех финансовых рынков - состоит в том, чтобы обеспечивать наличие механизма для привлечения инвестиций в экономику путем установления необходимых контактов между теми, кто нуждается в средствах, и теми, кто хотел бы инвестировать ...
0 комментариев