Навигация
Подведение под знак дифференциала
35065
знаков
3
таблицы
40
изображений
2. Подведение под знак дифференциала.
Пример 30.
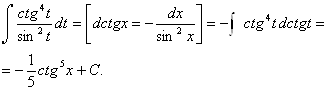
3. Метод замены переменной:
а) замена 
в интеграле
: 
,
где 
- функция, интегрируемая легче, чем исходная; 
- функция, обратная функции ; 
- первообразная функции 
.
Пример 31.
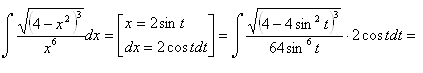
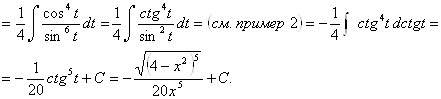
б) замена 
в интеграле вида:
;
Пример 32.
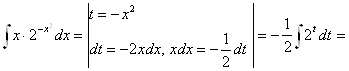
Пример 33.
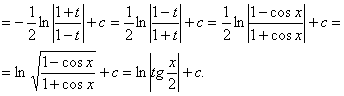
4. Метод интегрирования по частям:
Пример 34.
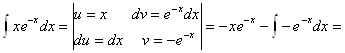
Пример 35.
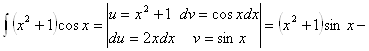
Возьмем отдельно интеграл
Вернемся к нашему интегралу:
Определение. Пусть на некотором интервале 
задана непрерывная функция 
. Построим ее график.
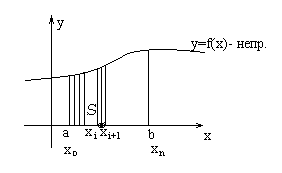
Фигура, ограниченная сверху кривой 
, слева и справа прямыми 
и снизу отрезком оси абсцисс между точками a и b, называется криволинейной трапецией.
S – область – криволинейная трапеция.
Разделим интервал точками 
и получим:
Интегральная сумма:
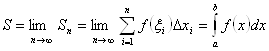
Определение. Определенным интегралом называется предел интегральной суммы.
Свойства определенного интеграла:
1. Постоянный множитель можно выносить за знак интеграла:
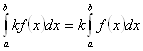
2. Интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов этих функций:
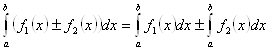
3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е. при любых a, b, c 
:
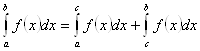
4. Если на отрезке 
, то и 
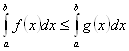
5. Пределы интегрирования можно менять местами, при этом меняется знак интеграла:
6. 
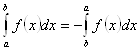
7. Интеграл в точке равен 0:
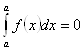
8. 
9. (“о среднем”) Пусть y = f(x) – функция, интегрируемая на [a,b]. Тогда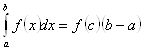 
, где 
, f(c) – среднее значение f(x) на [a,b]:
10. Формула Ньютона-Лейбница
,
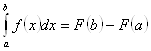где F(x) – первообразная для f(x).
3.2.2 Методы вычисления определенного интеграла.1. Непосредственное интегрирование
Пример 35.
а)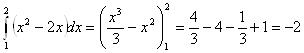 
б)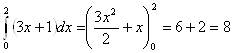 
в)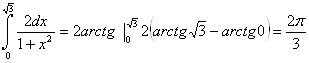 
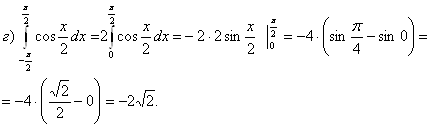
д)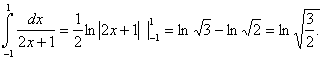 
Похожие работы
... , выражать свою позицию, рефлексировать собственное поведение, самостоятельно принимать решения и т.п.» [20, с.351]. Именно такие ситуации возможно создавать при проведении лабораторного практикума. Студент, выполняя самостоятельно творческое задание исследовательского характера, проходит от начала до конца путь исследователя, решающего реальную научную проблему. Пройдя такой путь несколько раз ...
... классики полезно вспомнить о потенциальном резерве времени, который объективно появляется при использовании систем автоматизации математических расчетов, и использовать этот резерв для резкого расширения круга изучаемых задач и методов вычислений. Незаменима роль системы Derive для интенсификации обучения при подготовке к вступительным экзаменам по математике. Ситуация известна: школьный курс ...
... перспективу. Вторая задача - оценка использования организациями своих материальных, трудовых и финансовых ресурсов. Наиболее рациональное и эффективное использование ресурсов - важнейшая экономическая задача. На основе экономического анализа дается оценка эффективности использования материальных, трудовых и финансовых ресурсов. В промышленности, например, в этом плане исследуются эффективность ...
... полностью. Структура найденного решения наиболее сильно зависит от реализации единицы продукции №1 и №3, а также от уменьшения или увеличения всех имеющихся ресурсов. Часть № 2 "Расчет экономико-математической модели межотраслевого баланса Теоретические положения. Балансовый метод - метод взаимного сопоставления финансовых, материальных и трудовых ресурсов и потребностям в них. Балансовая ...
0 комментариев