Навигация
1. Пределы.
Определение. Число A называется пределом функции ![]() при стремлении точки
при стремлении точки ![]() к точке
к точке ![]() , если для каждого сколь угодно малого числа
, если для каждого сколь угодно малого числа ![]() найдется такое число
найдется такое число ![]() , что для любой точки
, что для любой точки ![]() верно условие
верно условие ![]() , также верно условие
, также верно условие ![]() . Записывают:
. Записывают: ![]() .
.
Пример 41. Найти пределы:
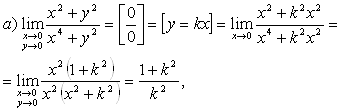
т.е. предел зависит от ![]() , а, значит, он не существует.
, а, значит, он не существует.
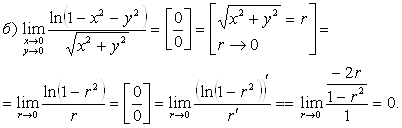
2. Непрерывность.
Определение. Пусть точка ![]() принадлежит области определения функции
принадлежит области определения функции ![]() . Тогда функция
. Тогда функция ![]() называется непрерывной в точке
называется непрерывной в точке ![]() , если
, если
![]() (1)
(1)
причем точка ![]() стремится к точке
стремится к точке ![]() произвольным образом.
произвольным образом.
Если в какой-либо точке условие (1) не выполняется, то эта точка называется точкой разрыва функции ![]() . Это может быть в следующих случаях:
. Это может быть в следующих случаях:
1) Функция ![]() не определена в точке
не определена в точке ![]() .
.
2) Не существует предел ![]() .
.
3) Этот предел существует, но он не равен ![]() .
.
Пример 42. Определить, является ли данная функция ![]() непрерывной в точке
непрерывной в точке ![]() , если
, если ![]() .
.

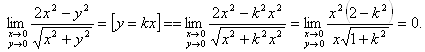
Получили, что ![]() значит, данная функция непрерывна в точке
значит, данная функция непрерывна в точке ![]() .
.
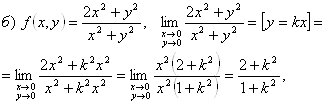
предел зависит от k, т.е. он в данной точке не существует, а значит, функция имеет в этой точке разрыв.
4.3 Производные и дифференциалы функций нескольких переменных 4.3.1 Частные производные первого порядкаЧастная производная функции ![]() по аргументу x является обыкновенной производной функции одной переменной x при фиксированном значении переменной y и обозначается:
по аргументу x является обыкновенной производной функции одной переменной x при фиксированном значении переменной y и обозначается:
![]()
Частная производная функции ![]() по аргументу y является обыкновенной производной функции одной переменной y при фиксированном значении переменной x и обозначается:
по аргументу y является обыкновенной производной функции одной переменной y при фиксированном значении переменной x и обозначается:
![]()
Пример 43. Найти частные производные функций.

Частные производные второго порядка – это частные производные от частных производных первого порядка. Для функции двух переменных вида ![]() возможны четыре вида частных производных второго порядка:
возможны четыре вида частных производных второго порядка:
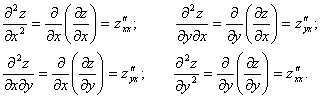
Частные производные второго порядка, в которых дифференцирование производится по разным переменным, называют смешанными производными. Смешанные производные второго порядка дважды дифференцируемой функции равны.
Пример 44. Найти частные производные второго порядка.
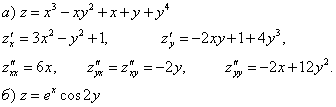
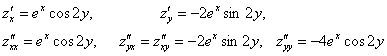

Определение. Дифференциал первого порядка функции двух переменных ![]() находится по формуле
находится по формуле
![]() .
.
Пример 45. Найти полный дифференциал для функции ![]() .
.
Решение. Найдем частные производные:
![]()
тогда
![]() .
.
При малых приращениях аргументов x и y функция ![]() получает приращение
получает приращение ![]() , приблизительно равное dz, т.е.
, приблизительно равное dz, т.е. ![]() .
.
Формула для нахождения приближенного значения функции ![]() в точке
в точке ![]() , если известно ее точное значение в точке
, если известно ее точное значение в точке ![]() :
:
![]() .
.
Пример 46. Найти ![]() .
.
Решение. Пусть ![]() ,
,
![]() .
.
Тогда используем формулу
![]() .
.
Получим:
![]() .
.
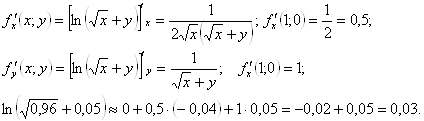
Ответ. ![]() .
.
Пример 47. Вычислить приближенно ![]() .
.
Решение. Рассмотрим функцию ![]() . Имеем
. Имеем
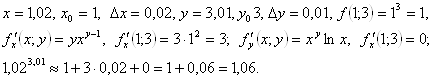
Ответ. ![]() .
.
Пример 48. Вычислить приближенно ![]() .
.
Решение. Рассмотрим функцию ![]() . Получим:
. Получим:
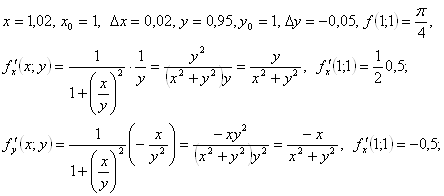
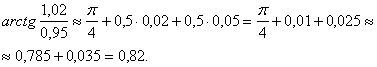
Ответ. ![]() .
.
Определение. Функция ![]() называется неявной, если она задается уравнением
называется неявной, если она задается уравнением ![]() , не разрешимым относительно z.
, не разрешимым относительно z.
Частные производные такой функции находятся по формулам:
![]()
Пример 49. Найти частные производные функции z, заданной уравнением ![]() .
.
Решение. 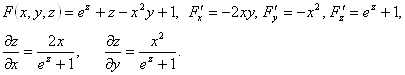
Определение. Функция ![]() называется неявной, если она задается уравнением
называется неявной, если она задается уравнением ![]() , не разрешимым относительно y.
, не разрешимым относительно y.
Производная такой функции находится по формуле:
![]() .
.
Пример 50. Найти производные данных функций.
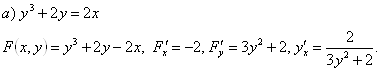
![]()
![]()
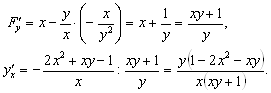
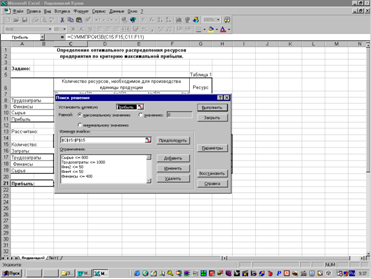
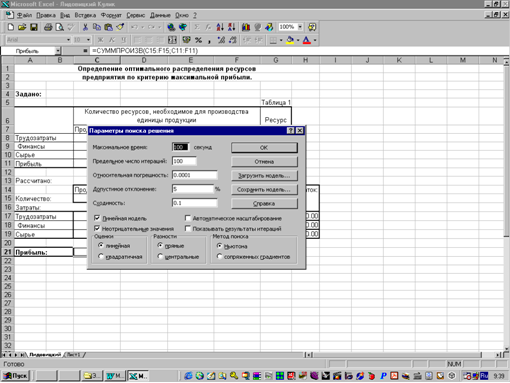
Глава 5. Классические методы оптимизации
Похожие работы
... , выражать свою позицию, рефлексировать собственное поведение, самостоятельно принимать решения и т.п.» [20, с.351]. Именно такие ситуации возможно создавать при проведении лабораторного практикума. Студент, выполняя самостоятельно творческое задание исследовательского характера, проходит от начала до конца путь исследователя, решающего реальную научную проблему. Пройдя такой путь несколько раз ...
... классики полезно вспомнить о потенциальном резерве времени, который объективно появляется при использовании систем автоматизации математических расчетов, и использовать этот резерв для резкого расширения круга изучаемых задач и методов вычислений. Незаменима роль системы Derive для интенсификации обучения при подготовке к вступительным экзаменам по математике. Ситуация известна: школьный курс ...
... перспективу. Вторая задача - оценка использования организациями своих материальных, трудовых и финансовых ресурсов. Наиболее рациональное и эффективное использование ресурсов - важнейшая экономическая задача. На основе экономического анализа дается оценка эффективности использования материальных, трудовых и финансовых ресурсов. В промышленности, например, в этом плане исследуются эффективность ...
... полностью. Структура найденного решения наиболее сильно зависит от реализации единицы продукции №1 и №3, а также от уменьшения или увеличения всех имеющихся ресурсов. Часть № 2 "Расчет экономико-математической модели межотраслевого баланса Теоретические положения. Балансовый метод - метод взаимного сопоставления финансовых, материальных и трудовых ресурсов и потребностям в них. Балансовая ...

0 комментариев