Навигация
Введение в математический анализ
1. Введение в математический анализ
Задача 1. Найти область определения функции.
1.![]()
2. 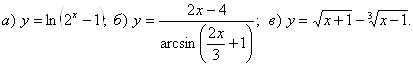
3. ![]()
4. ![]()
5. 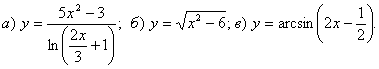
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()
Задача 2. Найти пределы функций.
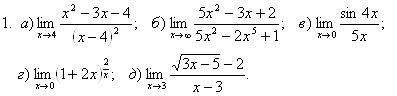


![]()
![]()
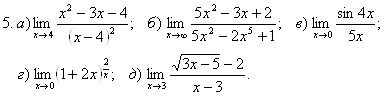
![]()
![]()
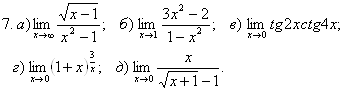

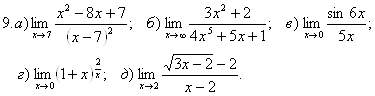
 .
.
Задача 3. Найти точки разрыва функции и определить их тип.
1. ![]() 2.
2. ![]() 3.
3. ![]()
4. ![]() 5.
5. ![]() 6.
6. ![]()
7. ![]() 8.
8. ![]() 9.
9. ![]() 10.
10. ![]()
Глава 2. Дифференциальное исчисление функции одной переменной
Задача 4. Найти производные данных функций.
1. а)![]() ; б)
; б) ![]() в) y =
в) y = ![]() ;
;
г) y = ![]() x6 +
x6 + ![]() +
+ ![]() + 5; д) y = x tg x + ln sin x + e3x;
+ 5; д) y = x tg x + ln sin x + e3x;
е) y = 2 x - arcsin x.
2. а) ![]() ; б) y =
; б) y = ![]()
![]() ; в) y =
; в) y = ![]() ; г) y =
; г) y = ![]() x2 –
x2 –![]() + 3; д) y = e cos
+ 3; д) y = e cos![]() ; е) y =
; е) y = ![]() .
.
3. а) y = ![]() lnx; б) y =
lnx; б) y =![]() ; в) y = ln
; в) y = ln ![]() ;
;
г) y = ![]() ; д) y =
; д) y = ![]() x7 +
x7 + ![]() + 1; е) y = 2
+ 1; е) y = 2![]() .
.
4. а) y = ![]() ; б) y = (e5x – 1)6; в) y =
; б) y = (e5x – 1)6; в) y = ![]() ; г) y =
; г) y = ![]() ; д) y =
; д) y = ![]() x8 +
x8 +![]() +
+ ![]() + 5; е) y = 3 x - arcsinx.
+ 5; е) y = 3 x - arcsinx.
5. а) y = 2x3 - ![]() + ex; б) y =
+ ex; б) y = ![]() ; в) y =
; в) y = ![]() ;
;
г) y = ![]()
![]() ; д) y = 2 cos
; д) y = 2 cos![]() ; е) y =
; е) y = ![]() .
.
6. а) y = ![]() lnx; б) y =
lnx; б) y =![]() ; в) y = ln
; в) y = ln ![]() ;
;
г) y = ![]() ; д) y =
; д) y = ![]() x7 +
x7 + ![]() + 1; е) y = 2
+ 1; е) y = 2![]() .
.
7. а) ![]() ; б) y =
; б) y = ![]()
![]() ; в)y =
; в)y = ![]() ; г)y = x2 + x sin x +
; г)y = x2 + x sin x + ![]() ; д) y = e cos
; д) y = e cos![]() ; е) y =
; е) y = ![]() .
.
8. а) y = ![]() ; б) y = (3x – 4)6; в) y = sin tg
; б) y = (3x – 4)6; в) y = sin tg ![]() ;
;
г) y = 3x4 – ![]() – 9
– 9![]() + 9; д) y =
+ 9; д) y = ![]() ;
;
е)y = x2 + arcsin x - x![]() .
.
9. а)![]() ; б)
; б)![]() ; в) y =
; в) y = ![]() ; г) y = 5 sin3x; д) y =
; г) y = 5 sin3x; д) y = ![]() x3 –
x3 – ![]() – 6
– 6![]() + 3; е) y = 4x 4
+ 3; е) y = 4x 4![]() + ln
+ ln![]() .
.
10. а) ![]() б) y =
б) y = ![]() ; в) y = (3x – 4)6; г) y =
; в) y = (3x – 4)6; г) y = ![]() ; д)y = x2 - x
; д)y = x2 - x![]() ; е) y = e sin3x + 2.
; е) y = e sin3x + 2.
Задача 5. Исследовать функцию и построить ее график.
1. а) ![]() б)
б) ![]() в)
в) ![]() .
.
2. а)![]() б)
б) ![]() в)
в) ![]() .
.
3. а)![]() б)
б) ![]() в)
в) ![]() .
.
4. ![]() б)
б) ![]() в)
в) ![]()
5. а)![]() б)
б) ![]() в)
в) ![]() .
.
6. а)![]() б)
б) ![]() в)
в) ![]() .
.
7. а)![]() б)
б)![]() в)
в) ![]() .
.
8. а)![]() б)
б) ![]() в)
в) ![]() .
.
9. а)![]() б)
б) ![]() в)
в) ![]() .
.
10. а)![]() б)
б) ![]() в)
в) ![]() .
.
Задача 6. Найти наибольшее и наименьшее значение функции на заданном отрезке.
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
4. ![]() .
.
5. ![]() .
.
6. ![]() .
.
7. ![]() .
.
8. ![]() .
.
9. ![]() .
.
10. ![]() .
.
Глава 3. Интегральное исчисление
Задача 7. Найти неопределенные интегралы.
1. а) ![]() б)
б)![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
2. а) 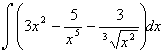 ;б)
;б)![]() в)
в) ![]() г)
г) ![]() .
.
3. 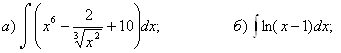
![]()
4. 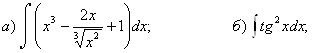
![]() г)
г)![]()
5. а)![]() ; б)
; б)![]() ; в)
; в) ![]() ; г)
; г)![]() .
.
6. а)![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]()
7. а) ![]() ; б)
; б) 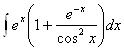 ; в)
; в) ![]() ; г)
; г) ![]()
8. а) 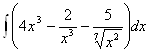 ; б)
; б)![]() ; в)
; в)![]() ; г)
; г) ![]() .
.
9. а) 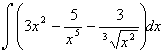 ; б)
; б) ![]() в)
в)![]() ; г)
; г)![]() .
.
10. а) ![]() б)
б)![]() в)
в) ![]() ; г)
; г) ![]() .
.
Задача 8. Вычислить определенные интегралы.
1. 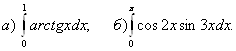
2. 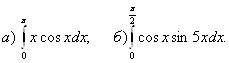
3. 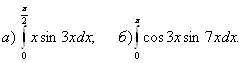
4. 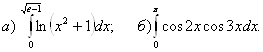
5. 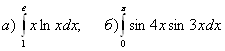
6. 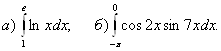
7. 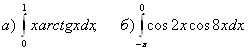 .
.
8. 
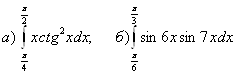
9. 
10. 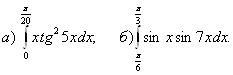
Задача 9. Найти несобственные интегралы или доказать, что они расходятся.
1. 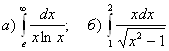 .
.
2. ![]() .
.
3. 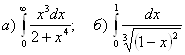 .
.
4. 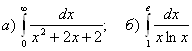 .
.
5. 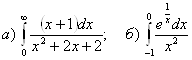 .
.
6. 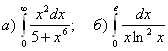 .
.
7. 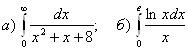 .
.
8. 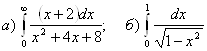 .
.
9.  .
.
10. 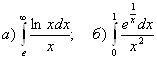 .
.
Задача 10. Найти площадь области, ограниченной кривыми
1. ![]() .2.
.2. ![]() .
.
3. ![]() 4.
4. ![]()
5. ![]() 6.
6. ![]()
7. ![]() ,
, ![]() .8.
.8.![]() .
.
9. ![]()
10. ![]() ,
, ![]() .
.
Глава 4. Дифференциальное исчисление функции нескольких переменных.
Задача 11. Найти область определения функции (показать на чертеже).
1. ![]()
2. 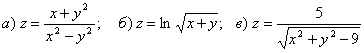 .
.
3. ![]() .
.
4. ![]()
5. ![]() .
.
6. 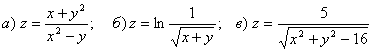 .
.
7. ![]() .
.
8. ![]() .
.
9. ![]() .
.
10. ![]()
Задача 12. Исследовать на непрерывность функции при
![]() и
и ![]() .
.
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()
Задача 13. Найти производную неявно заданной функции.
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
4. ![]() .
.
5. ![]() .
.
6. ![]() .
.
7. ![]() .
.
8. ![]() .
.
9. ![]() .
.
10. ![]() .
.
Задача 14. Вычислить приближенно
1. а) ![]() ;б)
;б) ![]() ; в)
; в) ![]()
2. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3. а)![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
4. а)![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
5. а)![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
6. а)![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
7. а)![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
8. а) ![]() ;б)
;б) ![]() ; в)
; в) ![]()
9. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
10. а) ![]() ;б)
;б) ![]() ; в)
; в) ![]()
Задача 15. Исследовать функцию на экстремумы.
1. ![]() .
.
2. ![]()
![]() .
.
3. ![]()
![]() .
.
4. ![]()
![]() .
.
5. ![]()
![]() .
.
6. ![]()
![]() .
.
7. ![]()
![]() .
.
8. ![]()
![]() .
.
9. ![]()
![]() .
.
10. ![]()
![]() .
.
Задача 16. Найти наибольшее и наименьшее значение функции ![]() в данной замкнутой области.
в данной замкнутой области.
1. ![]() в прямоугольнике
в прямоугольнике ![]()
2. ![]() в треугольнике, ограниченном осями координат и прямой
в треугольнике, ограниченном осями координат и прямой ![]()
3. ![]() в прямоугольнике
в прямоугольнике
![]()
4. ![]() в области, ограниченной параболой
в области, ограниченной параболой
![]() и осью абсцисс.
и осью абсцисс.
5. ![]() в квадрате
в квадрате ![]()
6. ![]() в треугольнике, ограниченном осями координат и прямой
в треугольнике, ограниченном осями координат и прямой ![]()
7. ![]() в треугольнике, ограниченном осями координат и прямой
в треугольнике, ограниченном осями координат и прямой ![]()
8. ![]() в треугольнике, ограниченном осями координат и прямой
в треугольнике, ограниченном осями координат и прямой ![]()
9. ![]() в области, ограниченной параболой
в области, ограниченной параболой
![]() и осью абсцисс.
и осью абсцисс.
10. ![]() в области, ограниченной параболой
в области, ограниченной параболой
![]() и осью абсцисс.
и осью абсцисс.
Литература
Основная
1. М.С. Красс, Б.П. Чупрынов. Основы математики и ее приложение в экономическом образовании: Учебник. – 4-е изд., исп. – М.: Дело, 2003.
2. М.С. Красс, Б.П. Чупрынов. Математика для экономических специальностей: Учебник. – 4-е изд., исп. – М.: Дело, 2003.
3. М.С. Красс, Б.П. Чупрынов. Математика для экономического бакалавриата. Учебник. – 4-е изд., исп. – М.: Дело, 2005.
4. Высшая математика для экономистов. Учебник для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; Под ред. проф. Н.Ш. Кремера, - 2-е изд., перераб. и доп. – М: ЮНИТИ, 2003.
5. Кремер Н.Ш, Путко Б.А., Тришин И.М., Фридман М.Н.. Высшая математика для экономических специальностей. Учебник и Практикум (части I и II) / Под ред. проф. Н.Ш. Кремера, - 2-е изд., перераб. и доп. – М: Высшее образование, 2007. – 893с. – (Основы наук)
6. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. М. высшая школа. 1999.
Дополнительная
1. И.И. Баврин, В.Л. Матросов. Высшая математика. «Гуманитарный издательский центр Владос», 2002.
2. И.А. Зайцев. Высшая математика. «Высшая школа», 1998.
3. А.С. Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандра. Математика в экономике / в двух частях/. М. Финансы и статистика. 1999.
Похожие работы
... , выражать свою позицию, рефлексировать собственное поведение, самостоятельно принимать решения и т.п.» [20, с.351]. Именно такие ситуации возможно создавать при проведении лабораторного практикума. Студент, выполняя самостоятельно творческое задание исследовательского характера, проходит от начала до конца путь исследователя, решающего реальную научную проблему. Пройдя такой путь несколько раз ...
... классики полезно вспомнить о потенциальном резерве времени, который объективно появляется при использовании систем автоматизации математических расчетов, и использовать этот резерв для резкого расширения круга изучаемых задач и методов вычислений. Незаменима роль системы Derive для интенсификации обучения при подготовке к вступительным экзаменам по математике. Ситуация известна: школьный курс ...
... перспективу. Вторая задача - оценка использования организациями своих материальных, трудовых и финансовых ресурсов. Наиболее рациональное и эффективное использование ресурсов - важнейшая экономическая задача. На основе экономического анализа дается оценка эффективности использования материальных, трудовых и финансовых ресурсов. В промышленности, например, в этом плане исследуются эффективность ...
... полностью. Структура найденного решения наиболее сильно зависит от реализации единицы продукции №1 и №3, а также от уменьшения или увеличения всех имеющихся ресурсов. Часть № 2 "Расчет экономико-математической модели межотраслевого баланса Теоретические положения. Балансовый метод - метод взаимного сопоставления финансовых, материальных и трудовых ресурсов и потребностям в них. Балансовая ...

0 комментариев