Навигация
Замена переменных под знаком определенного интеграла
2. Замена переменных под знаком определенного интеграла.
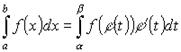
![]()
Пример 36.
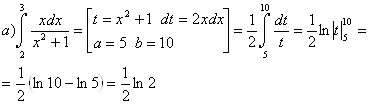
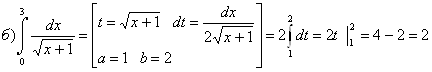
2. Интегрирование по частям в определенном интеграле.
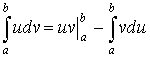
Пример 37.
а) 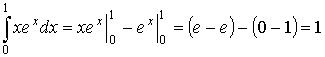
б) 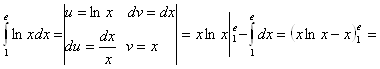
![]()
в) 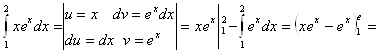
![]()
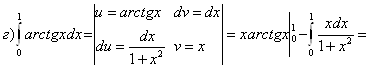
![]()
д) 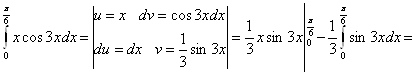
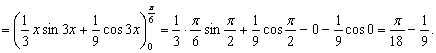
3.2.3 Приложения определенного интеграла
| Характеристика | Вид функции | Формула |
| площадь криволинейной трапеции | в декартовых координатах |
|
| площадь криволинейного сектора | в полярных координатах |
|
| площадь криволинейной трапеции | в параметрической форме |
|
| длина дуги кривой | в декартовых координатах |
|
| длина дуги кривой | в полярных координатах |
|
| длина дуги кривой | в параметрической форме |
|
| объём тела вращения | в декартовых координатах |
|
| объём тела с заданным поперечным сечением |
|
Пример 38. Вычислить площадь фигуры, ограниченной линиями: ![]() и
и ![]() .
.
Решение: Найдем точки пересечения графиков данных функций. Для этого приравняем функции и решим уравнение ![]()
Итак, точки пересечения ![]() и
и ![]() .
.

Площадь фигуры найдем, используя формулу
![]() .
.
В нашем случае
![]()
![]()
Ответ: площадь равна ![]() (квадратных единиц).
(квадратных единиц).
Глава 4. Функции нескольких переменных
4.1 Основные понятияОпределение. Если каждой паре независимых друг от друга чисел ![]() из некоторого множества по какому-либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных.
из некоторого множества по какому-либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных.
Определение. Областью определения функции z называется совокупность пар ![]() , при которых функция z существует.
, при которых функция z существует.
Область определения функции двух переменных ![]() представляет собой некоторое множество точек на координатной плоскости Oxy. Координата z называется аппликатой, и тогда сама функция изображается в виде некоторой поверхности в пространстве E3. Например:
представляет собой некоторое множество точек на координатной плоскости Oxy. Координата z называется аппликатой, и тогда сама функция изображается в виде некоторой поверхности в пространстве E3. Например:
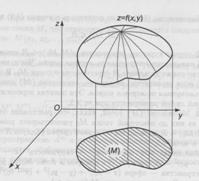
Рис.1
Пример 39. Найти область определения функции.
а) ![]()
Выражение, стоящее в правой части имеет смысл только при ![]() . Значит, область определения данной функции есть совокупность всех точек, лежащих внутри и на границе круга радиуса R с центром в начале координат.
. Значит, область определения данной функции есть совокупность всех точек, лежащих внутри и на границе круга радиуса R с центром в начале координат.

б) ![]() .
.
Область определения данной функции – все точки плоскости ![]() , кроме точек прямых
, кроме точек прямых ![]() , т.е. осей координат.
, т.е. осей координат.
Определение. Линии уровня функции ![]() – это семейство кривых на координатной плоскости
– это семейство кривых на координатной плоскости ![]() , описываемое уравнениями вида
, описываемое уравнениями вида ![]()
![]() .
.
Пример 40. Найти линии уровня функции ![]() .
.
Решение. Линии уровня данной функции – это семейство кривых на плоскости ![]() , описываемое уравнением
, описываемое уравнением
![]() , или
, или ![]() .
.
Последнее уравнение описывает семейство окружностей с центром в точке О1(1, 1) радиуса ![]() . Поверхность вращения (параболоид), описываемая данной функцией, становится «круче» по мере ее удаления от оси, которая задается уравнениями x = 1, y = 1. (Рис. 4)
. Поверхность вращения (параболоид), описываемая данной функцией, становится «круче» по мере ее удаления от оси, которая задается уравнениями x = 1, y = 1. (Рис. 4)
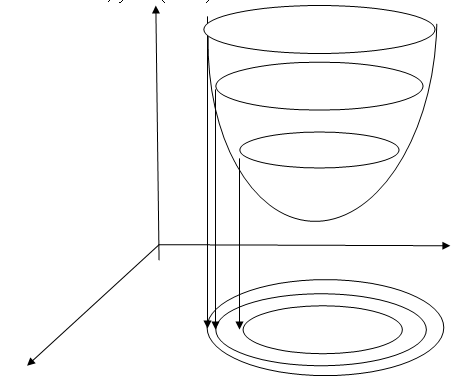
Рис.4
4.2 Пределы и непрерывность функций нескольких переменных.Похожие работы
... , выражать свою позицию, рефлексировать собственное поведение, самостоятельно принимать решения и т.п.» [20, с.351]. Именно такие ситуации возможно создавать при проведении лабораторного практикума. Студент, выполняя самостоятельно творческое задание исследовательского характера, проходит от начала до конца путь исследователя, решающего реальную научную проблему. Пройдя такой путь несколько раз ...
... классики полезно вспомнить о потенциальном резерве времени, который объективно появляется при использовании систем автоматизации математических расчетов, и использовать этот резерв для резкого расширения круга изучаемых задач и методов вычислений. Незаменима роль системы Derive для интенсификации обучения при подготовке к вступительным экзаменам по математике. Ситуация известна: школьный курс ...
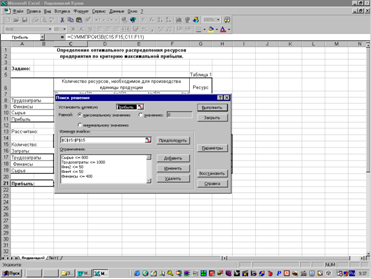
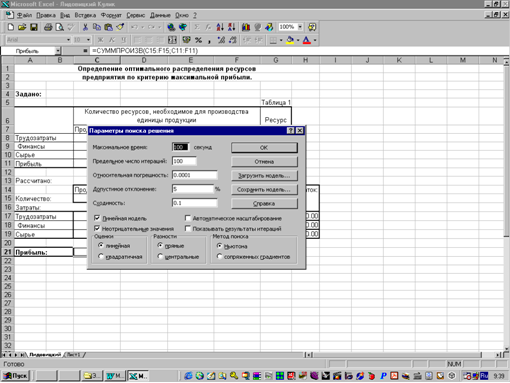
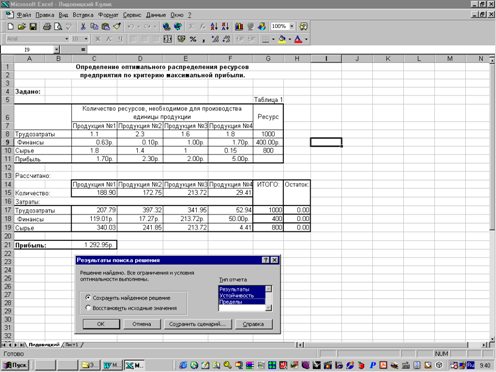
... перспективу. Вторая задача - оценка использования организациями своих материальных, трудовых и финансовых ресурсов. Наиболее рациональное и эффективное использование ресурсов - важнейшая экономическая задача. На основе экономического анализа дается оценка эффективности использования материальных, трудовых и финансовых ресурсов. В промышленности, например, в этом плане исследуются эффективность ...
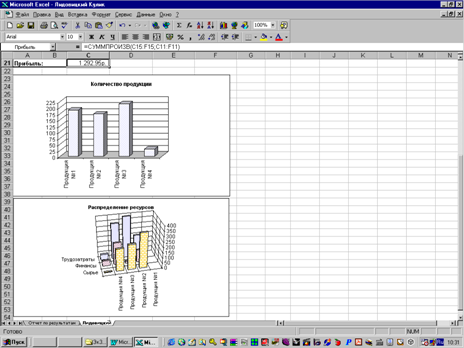
... полностью. Структура найденного решения наиболее сильно зависит от реализации единицы продукции №1 и №3, а также от уменьшения или увеличения всех имеющихся ресурсов. Часть № 2 "Расчет экономико-математической модели межотраслевого баланса Теоретические положения. Балансовый метод - метод взаимного сопоставления финансовых, материальных и трудовых ресурсов и потребностям в них. Балансовая ...
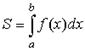
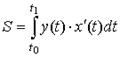
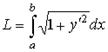
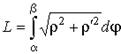
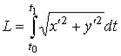
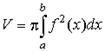

0 комментариев