Локальный экстремум функции нескольких переменных

5.1 Локальный экстремум функции нескольких переменных

Определение 1. Функция  имеет максимум в точке , если  для всех точек  достаточно близких к точке  и отличных от нее.

Определение 2. Функция  имеет минимум в точке , если  для всех точек  достаточно близких к точке  и отличных от нее.

Необходимое условие экстремума. Если функция достигает экстремума в точке , то частные производные от функции  обращаются в нуль или не существуют в этой точке.

Точки, в которых частные производные обращаются в нуль или не существуют, называются критическими.

Достаточный признак экстремума. Пусть функция определена в некоторой окрестности критической точки  и имеет в этой точке непрерывные частные производные второго порядка

Тогда

1)  имеет локальный максимум в точке , если и ;

2)  имеет локальный минимум в точке , если и ;

3)  не имеет локального экстремума в точке , если ;

Схема исследования на экстремум функции двух переменных.

1.  Найти частные производные функции : и .

2.  Решить систему уравнений ,  и найти критические точки функции.

3.  Найти частные производные второго порядка, вычислить их значения в критических точках и с помощью достаточного условия сделать вывод о наличии экстремумов.

4.  Найти экстремумы функции.

Пример 51. Найти экстремумы функции .

Решение.

1)  Найдем частные производные .

2)  Решим систему уравнений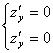

3) 

4)  Найдем частные производные второго порядка и их значения в критических точках: . В точке  получим:

 

значит, в точке  экстремума нет. В точке  получим:

 

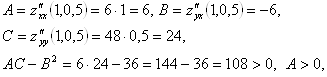
значит, в точке  минимум.

5)  .

Ответ.

  5.2 Глобальный экстремум (наибольшее и наименьшее значение функции)

Наибольшее и наименьшее значения функции нескольких переменных, непрерывной на некотором замкнутом множестве, достигаются или в точках экстремума, или на границе множества.

Схема нахождения наибольшего и наименьшего значений.

1)  Найти критические точки, лежащие внутри области, вычислить значение функции в этих точках.

2)  Исследовать функцию на границе области; если граница состоит из нескольких различных линий, то исследование необходимо провести для каждого участка отдельно.

3)  Сравнить полученные значения функции и выбрать наибольшее и наименьшее.

Пример 52. Найти наибольшее и наименьшее значения функции  в прямоугольнике  .

Решение. 1) Найдем критические точки функции, для этого найдем частные производные: , и решим систему уравнений:

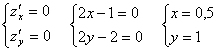
Получили критическую точку A. Полученная точка лежит внутри заданной области,

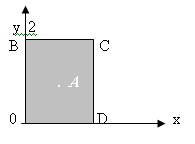
Границу области составляют четыре отрезка:  и. найдем наибольшее и наименьшее значение функции на каждом отрезке.

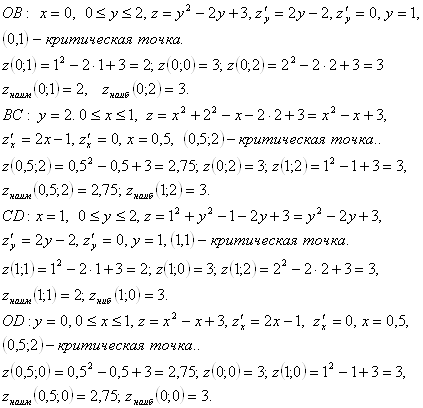
4)  Сравним полученные результаты и получим, что  в точках .

Глава 6. Модель потребительского выбора

Будем полагать, что имеется n различных товаров. Тогда некоторый набор товаров будем обозначать через n-мерный вектор , где  – количество i-того товара. Множество всех наборов товаров X называется пространством.

Выбор индивида-потребителя характеризуется отношением предпочтения: считается, что потребитель может сказать о любых двух наборах, какой более желателен, или он не видит между ними разницы. Отношение предпочтения транзитивно: если набор  предпочтительнее набора , а набор  предпочтительнее набора , то набор  предпочтительнее набора . Будем полагать, что поведение потребителя полностью описывается аксиомой индивида-потребителя: каждый индивид-потребитель принимает решение о потреблении, покупках и т.п., исходя из своей системы предпочтений.

  6.1 Функция полезности

На множестве потребительских наборов X определена функция , значение которой на потребительском наборе  равно потребительской оценке индивида для этого набора. Функция  называется функцией полезности потребителя или функцией потребительского предпочтения. Т.е. каждый потребитель имеет свою функцию полезности. Но все множество потребителей можно разделить на определенные классы потребителей (по возрасту, имущественному положению и т.п.) и каждому классу приписать некоторую, может быть, осредненную функцию полезности.

Т.о., функция  является потребительской оценкой или уровнем удовлетворения потребностей индивида при приобретении данного набора . Если набор  предпочтительнее набора  для данного индивида, то .

Свойства функции полезности.

1.

Первые частные производные функции полезности называются предельными полезностями продуктов. Из этого свойства следует, что возрастание потребления одного продукта при неизменном потреблении других продуктов приводит к росту потребительской оценки. Вектор 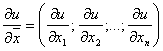 является градиентом функции , он показывает направление наибольшего роста функции. Для функции  ее градиент представляет собой вектор предельных полезностей продуктов.

2.

Т.е. предельная полезность любого товара уменьшается с ростом потребления.

3.

Т.е. предельная полезность каждого продукта увеличивается с ростом количества другого продукта.

Некоторые виды функций полезности.

1)  Неоклассическая: .

2)  Квадратическая: , где матрица отрицательно определена и  для .

3)  Логарифмическая функция: .

  6.2 Линии безразличия

В прикладных задачах и моделях потребительского выбора часто используется частный случай набора из двух товаров, т.е. когда функция полезности зависит от двух переменных. Линия безразличия – это линия, соединяющая потребительские наборы, имеющие один и тот же уровень удовлетворения потребностей индивида. По сути своей линии безразличия представляют собой линии уровня функции . Уравнения линий безразличия: .

Основные свойства линий безразличия.

1.  Линии безразличия, соответствующие разным уровням удовлетворения потребностей, не касаются и не пересекаются.

2.  Линии безразличия убывают.

3.  Линии безразличия выпуклы вниз.

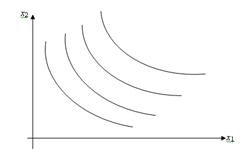
Из свойства 2 следует важное приближенное равенство .

Это соотношение показывает, на сколько индивид должен увеличить (уменьшить) потребление второго продукта при уменьшении (увеличении) потребления первого продукта на одну единицу без изменения уровня удовлетворения своих потребностей. Отношение  называется нормой замены первого продукта вторым, а величина  – предельной нормой замены первого продукта вторым.

Пример 53. Если предельная полезность первого товара равна 6, а второго – 2, то при уменьшении потребления первого товара на единицу нужно увеличить потребление второго товара на 3 единицы при том же уровне удовлетворения потребностей.

  6.3 Бюджетное множество

Пусть  – вектор цен на набор из n продуктов ; I – доход индивида, который он готов потратить на приобретение набора продуктов . Множество наборов товаров стоимостью не более I при данных ценах  называется бюджетным множеством B. При этом множество наборов стоимостью I называется границей G бюджетного множества B. Т.о. множество B ограничено границей G и естественными ограничениями .

Бюджетное множество описывается системой неравенств:

.

Рис. 1

Для случая набора из двух товаров бюджетное множество B (рис. 1) представляет собой треугольник в системе координат , ограниченный осями координат и прямой .

6.4 Теория потребительского спроса

В теории потребления полагается, что потребитель всегда стремится максимизировать свою полезность и единственным ограничением для него является ограниченность дохода I, который он может потратить на покупку набора товаров. В общем виде задача потребительского выбора (задача рационального поведения потребителя на рынке) формулируется следующим образом: найти потребительский набор , который максимизирует его функцию полезности при заданном бюджетном ограничении. Математическая модель этой задачи:

 

В случае набора из двух товаров:

Геометрически решение этой задачи – это точка касания границы бюджетного множества G и линии безразличия.

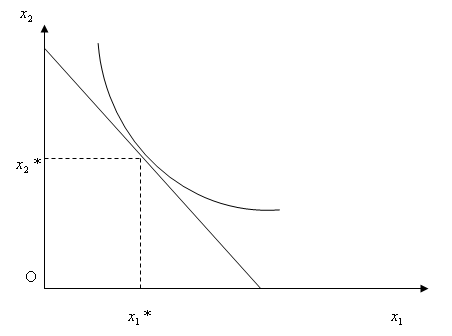
Решение этой задачи сводится к решению системы уравнений:

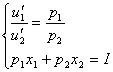(1)

Решение этой системы  является решением задачи потребительского выбора.

Решение задачи потребительского выбора  называется точкой спроса. Эта точка спроса зависит от цен  и дохода I. Т.е. точка спроса является функцией спроса. В свою очередь функция спроса – это набор n функций, каждая из которых зависит от  аргумента:

Эти функции называются функциями спроса соответствующих товаров.

Пример 54. Для набора из двух товаров на рынке, известных ценах на них  и  и дохода I найти функции спроса, если функция полезности имеет вид .

Решение. Продифференцируем функцию полезности:

.

Подставим полученные выражения в (1) и получим систему уравнений:

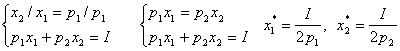
В данном случае расход на каждый товар составит половину дохода потребителя, а количество приобретенного товара равно затраченной на него сумме, поделенной на цену товара.

Пример 55. Пусть функция полезности для первого товара , второго ,

цена первого товара , цена второго . Доход . Какое количество товара должен приобрести потребитель, чтобы максимизировать полезность?

Решение. Найдем производные функций полезности, подставим в систему (1) и решим ее:

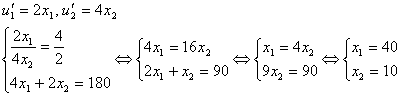
Этот набор товаров является оптимальным для потребителя с точки зрения максимизации полезности.

Задания для домашней контрольной работы

Контрольная работа должна быть выполнена в соответствии с вариантом, выбираемым по последней цифре номера зачетной книжки в отдельной тетради. Каждая задача должна содержать условие, подробное решение и вывод.