Навигация
Интеграл от суммы, есть сумма интегралов;
1. интеграл от суммы, есть сумма интегралов;
2. вынесение const за знак интеграла.
Можно сделать вывод: оператор А является линейным.
3) Проверим, является ли А непрерывным, для этого воспользуемся определением непрерывности:
p (fn(t), f0(t)) ![]() 0
0 ![]() p (A fn(t), Af0(t))
p (A fn(t), Af0(t)) ![]() 0.
0.
Оператор А, действует в пространстве C[a,b], в котором расстояние между функциями определяется следующим образом:
p (fn(t), f0(t)) = ![]() | fn(t) - f0(t)|.
| fn(t) - f0(t)|.
Решение:
p (A fn(t), Af0(t)) = ![]() |
|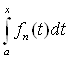 -
- 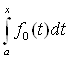 |.
|.
|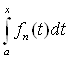 -
- 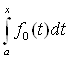 | = |
| = |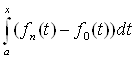 |
| ![]()
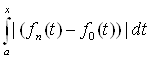
![]()
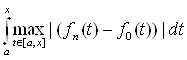 = p (fn(t), f0(t))
= p (fn(t), f0(t)) ![]() = p (fn(t), f0(t)) (x-a)
= p (fn(t), f0(t)) (x-a) ![]() 0
0
a![]() x
x![]() b.
b.
Таким образом p (A fn(t), Af0(t)) ![]() 0. следовательно по определению 2 оператор А непрерывен.
0. следовательно по определению 2 оператор А непрерывен.
4) Непрерывный оператор является ограниченным (теорема 3):
|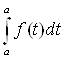 |
| ![]() |
|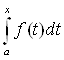 |
| ![]() |
|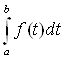 |
|
|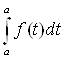 | = 0; |
| = 0; |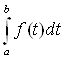 | = |b-a|.
| = |b-a|.
0 ![]() |
|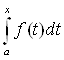 |
| ![]() |b-a|.
|b-a|.
5) Оператор А ограниченный, следовательно у него можно найти норму. Найдем норму оператора А (используя определение ||A||=![]() |A(f)|):
|A(f)|):
||A|| = ![]() |A(f)| =
|A(f)| = ![]() |
|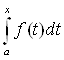 |
| ![]()
![]()
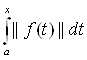
![]()
![]()
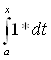 = (x-a);
= (x-a);
a ![]() x
x ![]() b;
b;
Норма оператора А: ||A|| = (b-a);
6) Обратимость интегрального оператора и его спектр.
Возьмем пространство S = {f ![]() C[0,b] / f(0) = 0} с нормой ||f|| =
C[0,b] / f(0) = 0} с нормой ||f|| = ![]() |f(x)|.
|f(x)|.
В пространстве S рассмотрим оператор А:
Аf = 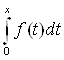
x ![]() [0,b], t
[0,b], t ![]() [0,x];
[0,x];
Найдем оператор обратный к (A - ![]() *I),
*I), ![]()
![]() R;
R;
(A - ![]() *I)*f = g
*I)*f = g
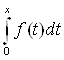 -
- ![]() *f(x) = g(x) (1)
*f(x) = g(x) (1)
Пусть функции f и g дифференцируемы;
Продифференцируем уравнение (1), получим:
f - ![]() *f/ = g/ (2)
*f/ = g/ (2)
Это уравнение (2) – дифференциальное неоднородное линейное уравнение. Решим это уравнение, используя метод Бернулли.
![]() - f/ =
- f/ = ![]()
![]() -
- ![]() + f/ = 0 (3)
+ f/ = 0 (3)
Представим решение уравнения в виде: f(x) = U(x)*V(x), тогда уравнение (3) примет вид:
![]() -
- ![]() *U*V + U/ *V + U*V/ = 0
*U*V + U/ *V + U*V/ = 0
U/ *V + U*V/ - ![]() *U*V = -
*U*V = - ![]()
U/ *V + U*(V/ - ![]() *V) = -
*V) = - ![]() (4)
(4)
Решаем однородное линейное уравнение:
V/ - ![]() *V = 0
*V = 0
V/ = ![]() *V
*V
![]() =
= ![]() *V
*V
![]() =
= ![]()
LnV = ![]() + c
+ c
V = ![]() *
*![]() , пусть
, пусть ![]() = с1
= с1
V = с1*![]()
Подставим частное решение однородного уравнения в уравнение (4) при условии, что V/ - ![]() *V = 0.
*V = 0.
Получим уравнение:
U/ * с1*![]() = -
= - ![]()
![]() = -
= -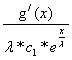
![]() = -
= - ![]() *
*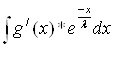
U = -![]() *
*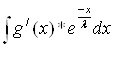
Подставим U и V в f(x) = U(x)*V(x) и получим:
f(x) = с1*![]() *(-
*(-![]() )*
)*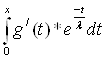
найдем интеграл Y = 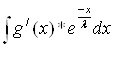 , интегрируем по частям:
, интегрируем по частям:
dz = g/(x)dx;
z = 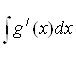 = g(x);
= g(x);
j = ![]() ;
;
dj = - ![]() *
*![]() dx;
dx;
Y = g(x)* ![]() +
+ ![]() *
*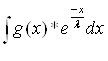
Подставим полученное значение в выражение f(x), которое примет вид:
f(x) = -![]() -
- ![]() *
*![]() *
*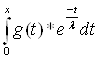 ;
;
Получим оператор В:
Bg = -![]() -
- ![]() *
*![]() *
*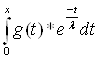 ;
;
x ![]() [0,b], t
[0,b], t ![]() [0,x], g(x)
[0,x], g(x) ![]() S,
S, ![]() - произвольное число.
- произвольное число.
Оператор В не существует, если ![]() = 0;
= 0;
Рассмотрим ограниченность оператора В для всех ![]()
![]() R,
R, ![]()
![]() 0;
0;
||Bg|| = ||f(x)|| = ![]() |f(x)| =
|f(x)| = ![]() |-
|-![]() -
- ![]() *
*![]() *
*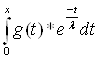 |
| ![]()
![]() (|
(|![]() | + |
| + |![]() *
*![]() *
*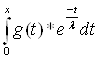 |)
|) ![]()
![]() |
|![]() | +
| + ![]() |
|![]() *
*![]() *
*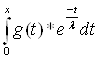 |
| ![]()
![]() |
|![]() | +
| + ![]() |
|![]() *
*![]() |*
|*![]() |g(x)*
|g(x)* ![]() |*|x|
|*|x| ![]()
![]() *
*![]() |g(x)| +
|g(x)| + ![]()
![]()
![]() *
*![]() |g(x)|*
|g(x)|* ![]() (|
(|![]() |*|x|)
|*|x|) ![]()
![]() |g(x)|*(
|g(x)|*( ![]() +
+ ![]() *
*![]()
![]() *
*![]()
![]() *b);
*b);
При ![]() > 0
> 0
![]()
![]() =
= ![]() ;
;
![]()
![]() = 1;
= 1;
При ![]() < 0
< 0
![]()
![]() =1;
=1;
![]()
![]() =
= ![]() ;
;
Эти оба случая можно записать в общем виде: ![]() {1,
{1, ![]() }, тогда
}, тогда
![]() |g(x)|*(
|g(x)|*( ![]() +
+ ![]() *
*![]()
![]() *
*![]()
![]() *b)
*b) ![]()
![]() |g(x)|*(
|g(x)|*( ![]() +
+ ![]() *
*![]() {1,
{1, ![]() }*b) = ||g(x)||*(
}*b) = ||g(x)||*( ![]() +
+ ![]() *
*![]() {1,
{1, ![]() }*b);
}*b);
Итак:
||Bg|| ![]() ||g(x)||*(
||g(x)||*( ![]() +
+ ![]() *
*![]() {1,
{1, ![]() }*b);
}*b);
То есть В – ограничен.
Осталось проверить, что В – оператор, обратный к (A - ![]() *I).
*I).
Если это так, то произведение этих операторов равно единичному оператору или же (A - ![]() *I)*(Bg) = g(x).
*I)*(Bg) = g(x).
Итак, нужно доказать, что
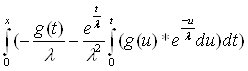 + g(x) +
+ g(x) + ![]() *
*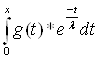 = g(x)
= g(x)
или
-![]() *
*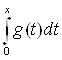 -
- ![]()
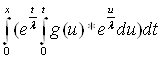 +
+ ![]() *
*![]() *
*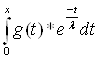 = 0; (*)
= 0; (*)
Возьмем производную от левой части (*) и получим:
-![]() *g(x) -
*g(x) - ![]() *
*![]() *
*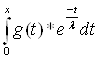 +
+ ![]() *
*![]() *
*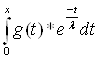 +
+ ![]() *
*![]() *
*![]() * g(x) = -
* g(x) = -![]() *g(x) +
*g(x) + ![]() *g(x) -
*g(x) - ![]() *
*![]() *
*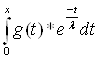 +
+ ![]() *
*![]() *
*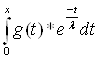 = 0;
= 0;
Следовательно, выражение (*) = const. Но, так как при x=0 выражение (*) (точнее его левая часть) равно 0, то и const=0. Значит В – обратный оператор к (A - ![]() *I) в S.
*I) в S.
Итак, мы получили ограниченный оператор В, обратный к (A - ![]() *I), который существует при
*I), который существует при ![]()
![]()
![]() R, за исключением
R, за исключением ![]() =0, то есть все возможные
=0, то есть все возможные ![]()
![]() 0 – это регулярные точки оператора А; Сам же оператор В – резольвента оператора А. Спектр оператора А – значение
0 – это регулярные точки оператора А; Сам же оператор В – резольвента оператора А. Спектр оператора А – значение ![]() при которых В не существует, то есть
при которых В не существует, то есть ![]() =0.
=0.
Вывод:
Оператор интегрирования, действующий в пространстве непрерывных функций – C[a,b], определенных на отрезке [a,b], заданный следующим образом: Аf(t) = 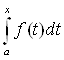 , где f(t) – функция, непрерывная на [a, b], t
, где f(t) – функция, непрерывная на [a, b], t ![]() [a,x]; x
[a,x]; x ![]() [a,b]; a,b
[a,b]; a,b![]() R:
R:
1. линейный;
2. непрерывный;
3. ограниченный: 0 ![]() |
|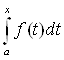 |
| ![]() |b-a|;
|b-a|;
Похожие работы
... понятия собственного числа линейного оператора А. 120. Определите, каким является базис а=(1/, 1/,1/), b=(1/, -1/, 0), с =(1/, 1/,-2/). Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету ЛИНЕЙНАЯ АЛГЕБРА Билет № 26 121. Приведение матрицы к ступенчатому виду методом Гаусса. Пример. 122. ...
... и1 и и2, соответствующие различным собственным значениям λ1 и λ2, ортогональны. Действительно, из соотношений Lu1 = λ1 и1, Lu2 = λ2и2, из вещественности λ1 и λ2 и из эрмитовости оператора L получаем цепочку равенств λ1(и1,и2) = (λ и1,и2) = (Lи1,и2) = (и1,Lu2) = (и1,λ2и2) = =λ2(и1,и2), т.е. λ1(и1,и2) = λ2(и1,и2). Отсюда, ...
... , называется оператором сдвига, если он каждую последовательность вида (х1,х2,…, хn…) переводит в последовательность вида (0, х1, х2, …, хn…), т.е. выполняется равенство: (х1,х2,…, хn…)=(0, х1, х2, …, хn…). Можно также рассматривать оператор сдвига, который действует в пространстве последовательностей, бесконечных в обе стороны. Элемент этого пространства можно представить в таком виде: (…х-2, ...
... состоит из значений функции g(x) на отрезке [a,b]. Причём этот оператор имеет лишь непрерывный спектр, так как резольвента при существует, но не непрерывна. Точечного спектра оператор не имеет. Пример 3: Рассмотрим оператор дифференцирования на множестве дифференцируемых функций. А: (для краткости будем писать вместо f(x) просто f). Рассмотрим резольвенту этого оператора: , то есть мы должны ...


0 комментариев