Навигация
4. норма A: ||A|| = (b-a);
5. резольвента оператора А: R![]() (A) = -
(A) = -![]() -
- ![]() *
*![]() *
*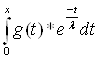 , где
, где
x ![]() [0,b], t
[0,b], t ![]() [0,x], g(x)
[0,x], g(x) ![]() S, S = {f
S, S = {f ![]() C[0,b] / f(0) = 0} с нормой ||f||=
C[0,b] / f(0) = 0} с нормой ||f||=![]() |f(x)|, g(x) =
|f(x)|, g(x) = 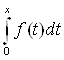 -
- ![]() *f(x),
*f(x), ![]() - произвольное число.
- произвольное число.
6. Спектр оператора А: ![]() =0.
=0.
§6. Оператор дифференцирования.
Рассмотрим оператор дифференцирования Д действующий в пространстве дифференцируемых функций – D[a,b], заданный следующим образом:
Дf(x) = f/(x);
Функция f(x) ![]() D[a, b], f/(x)
D[a, b], f/(x) ![]() C[a, b];
C[a, b];
Проверим оператор Д на линейность, по определению 1:
1) Аксиома аддитивности: Д(f+g) = Д(f) + Д(g).
Д(f+g) = (f+g)/ = f/ + g/ = Д(f) + Д(g).
2) Аксиома однородности: Д(kf) = kД(f).
Д(kf) = (kf) / = k(f)/ = kД(f).
Исходя из свойств производной:
1. производная от алгебраической суммы нескольких функций равна алгебраической сумме их производных;
2. постоянный множитель можно вынести за знак производной.
Можно утверждать, что Д – линейный оператор.
3) Для линейных операторов ограниченность и непрерывность оператора эквивалентны, это следует из теоремы 3.
3.1) Для начала покажем, что Д не является непрерывным оператором.
Задан оператор Дf(x) = f/(x) подпространства E ![]() C[0, 2
C[0, 2![]() ], состоящего из непрерывно дифференцируемых функций, в пространство C[0, 2
], состоящего из непрерывно дифференцируемых функций, в пространство C[0, 2![]() ].
].
Рассмотрим f0(x) = 0 ![]() C[0, 2
C[0, 2![]() ] и последовательность функций fn(x)=
] и последовательность функций fn(x)=![]() .
.
В пространстве E ![]() C[0, 2
C[0, 2![]() ]: p (f0, fn) =
]: p (f0, fn) = ![]() |
|![]() | =
| = ![]()
![]() 0, следовательно fn
0, следовательно fn ![]() f0.
f0.
Рассмотрим последовательность образов: Д(fn) = cos(nx).
Имеем:
p (Дfn, Дf0) = ![]() |cos(nx)|
|cos(nx)| ![]()
![]() = 1.
= 1.
Это означает, что Дfn не может сходиться к Дf0 , то есть отображение Д терпит разрыв в f0.
Поскольку оператор не является непрерывным, то, следовательно, он и не является ограниченным.
3.2) Теперь покажем, как из неограниченности оператора следует его разрывность.
Пусть оператор Д действует из C[0, 1] в C[0, 1], оператор Дf(x) = f/(x);
Этот оператор определен не на всем пространстве непрерывных функций, а лишь на подпространстве непрерывных функций, имеющих непрерывную производную.
В пространстве C[0, 1] норма ||f|| = ![]() |f(t)|.
|f(t)|.
Возьмем из C[0, 1] последовательность fn(t) = tn. Она ограничена в C[0, 1]: ||fn(t)|| = ![]() |tn| = 1.
|tn| = 1.
Рассмотрим Д fn(t): Д fn(t) = f/n(t) = n tn-1;
||f/n(t)|| = ![]() |n tn-1| = n.
|n tn-1| = n.
В результате получили, что оператор Д переводит ограниченное множество в неограниченное, значит, по определению этот оператор не является ограниченным, а по теореме 3 не является непрерывным.
Вывод:
Оператор дифференцирования Д действующий в пространстве дифференцируемых функций – D[a,b], заданный следующим образом: Дf(x)=f/(x), где функция f(x) ![]() D[a, b], f/(x)
D[a, b], f/(x) ![]() C[a, b]:
C[a, b]:
1. линейный;
2. не ограниченный;
3. не непрерывный.
§7. Оператор сдвига
Рассмотрим оператор А, действующий в пространстве непрерывных и ограниченных функций – C[![]() ], заданный следующим образом:
], заданный следующим образом:
Af(x) = f(x+a).
Функции f(x), f(x+a) ![]() C[
C[![]() ], a
], a ![]() R, f(x+a) – непрерывная и ограниченная функция.
R, f(x+a) – непрерывная и ограниченная функция.
Покажем линейность оператора А, по определению 1 должны выполняться следующие аксиомы :
1) Аксиома аддитивности: А(f+g) = А(f) + А(g).
А(f+g) = (f+g)(x+a) = f(x+a) + g(x+a) = А(f) + А(g).
По определению суммы функции, аксиома верна.
2) Аксиома однородности: А(kf) = kА(f).
A(k*f(x)) = k*f(x+a) = k*A(f(x)).
Аксиомы 1 и 2 верны, следовательно можно сделать вывод, что А – линейный оператор.
3) Проверим является ли оператор A непрерывным, для этого воспользуемся определением непрерывности:
p (fn(x), f0(x)) ![]() 0
0 ![]() p (A fn(x), Af0(x))
p (A fn(x), Af0(x)) ![]() 0.
0.
Оператор А действует в пространстве C[![]() ], в котором расстояние между функциями определяется следующим образом:
], в котором расстояние между функциями определяется следующим образом:
p (fn(x), f0(x)) = ![]() | fn(x) - f0(x)|.
| fn(x) - f0(x)|.
Решение:
p (A fn(x), Af0(x)) = ![]() |Afn(x) - Af0(x)| =
|Afn(x) - Af0(x)| = ![]() |fn(x+a) - f0(x+a)| =
|fn(x+a) - f0(x+a)| = 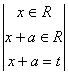 =
= ![]() |fn(t) - f0(t)| = p (fn(t), f0(t))
|fn(t) - f0(t)| = p (fn(t), f0(t)) ![]() 0.
0.
Таким образом p (A fn(x), Af0(x))
Похожие работы
... понятия собственного числа линейного оператора А. 120. Определите, каким является базис а=(1/, 1/,1/), b=(1/, -1/, 0), с =(1/, 1/,-2/). Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету ЛИНЕЙНАЯ АЛГЕБРА Билет № 26 121. Приведение матрицы к ступенчатому виду методом Гаусса. Пример. 122. ...
... и1 и и2, соответствующие различным собственным значениям λ1 и λ2, ортогональны. Действительно, из соотношений Lu1 = λ1 и1, Lu2 = λ2и2, из вещественности λ1 и λ2 и из эрмитовости оператора L получаем цепочку равенств λ1(и1,и2) = (λ и1,и2) = (Lи1,и2) = (и1,Lu2) = (и1,λ2и2) = =λ2(и1,и2), т.е. λ1(и1,и2) = λ2(и1,и2). Отсюда, ...
... , называется оператором сдвига, если он каждую последовательность вида (х1,х2,…, хn…) переводит в последовательность вида (0, х1, х2, …, хn…), т.е. выполняется равенство: (х1,х2,…, хn…)=(0, х1, х2, …, хn…). Можно также рассматривать оператор сдвига, который действует в пространстве последовательностей, бесконечных в обе стороны. Элемент этого пространства можно представить в таком виде: (…х-2, ...
... состоит из значений функции g(x) на отрезке [a,b]. Причём этот оператор имеет лишь непрерывный спектр, так как резольвента при существует, но не непрерывна. Точечного спектра оператор не имеет. Пример 3: Рассмотрим оператор дифференцирования на множестве дифференцируемых функций. А: (для краткости будем писать вместо f(x) просто f). Рассмотрим резольвенту этого оператора: , то есть мы должны ...


0 комментариев