Навигация
Формула для подсчета обратимых матриц порядка 2
25275
знаков
6
таблиц
4
изображения
1. Формула для подсчета обратимых матриц порядка 2.
Будем рассматривать матрицы 
.
Алгебраическое дополнение к элементу 
есть определитель матрицы 
порядка 1, т.е. 
. Алгебраическое дополнение к элементу 
есть определитель матрицы 
порядка 1, т.е. 
.
Нужно найти количество всех невырожденных матриц
(когда 
). При этом
(1.1)
Формулу выведем в 2 этапа.
1) Пусть 
(р-1 штук), 
(р-1 штук),
(по р штук) (1.2).
Тогда количество матриц, удовлетворяющих данным условиям, вычисляется по формуле
(р-1)2р2 (1.3)
Мы утверждаем, что по этой же формуле вычисляется количество матриц, определитель которых не обращается в нуль, при условии, что , .
В условии (1.2) не учитываются матрицы вида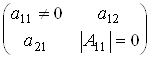 
с неравным нулю определителем, количество которых нужно прибавить.
Но сосчитали матрицы вида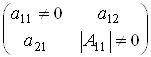 
с определителем обращающимся в нуль, количество которых нужно вычесть.
Докажем, что количество матриц в обоих случаях одинаково.
а) 
(р-1 штук), 
и . Из (1.1) получаем равенство 
. Значит 
. При заданном 
(где =1,2…р-1) элемент однозначно выражается через и 
(количество невырожденных матриц – р-1). Поэтому количество матриц удовлетворяющих этим условиям (р-1)3 штук.
б) , и 
. Значит 
. Отсюда 
. Элемент однозначно выражается через 
, , , которые принимаю не нулевые значения. Поэтому количество матриц удовлетворяющих этим условиям (р-1)3 штук
Значит формула (1.3) при условии (1.2) верна.
2) Пусть 
. Тогда 
, а из (1.1) получаем что и (как в первом этапе, случае а). Тогда количество таких матриц вычисляется по формуле
(р-1)2×р (1.4)
Этими этапами мы перебрали все случаи невырожденных матриц.
Складывая формулы (1.3) и (1.4) полученные в этапах 1) и 2) получаем формулу для нахождения количества обратимых матриц порядка 2 над полем Zp
(р-1)2×р×(р+1) (1.5)
Похожие работы
... гомоморфизм . K= - подгруппа Z и значит K=mZ для некоторого целого m. Отсюда следует, что H= . При этом и потому n=dm где d - целое. По теореме о гомоморфизме . Из доказанных теорем следует, что всякая подгруппа циклической группы циклична. Мы видим также, что для каждого целого d, делящего порядок n конечной циклической группы имеется и притом ровно одна подгруппа порядка d, то есть для ...
... но они не равны друг другу. Так будет, например, для подкольца , состоящего из матриц с нулевой последней строкой и последним столбцом; =diag(1,1,...,1,0) =diag(1,1,...,1). Определение. Гомоморфизмом колец называется отображение, сохраняющее обе кольцевые операции: и . Изоморфизм - это взаимно однозначный гомоморфизм. Ядро гомоморфизма - это ядро группового гомоморфизма аддитивных групп , то ...
... -x * y. Полем называется такое ассоциативное коммутативное кольцо с единицей k, в котором всякий ненулевой элемент обратим: . Таким образом, по определению в поле отсутствуют делители нуля. Кольцом называется множество с двумя алгебраическими операциями R (+, *), если: 0. Обратимыми называют те элементы кольца R, которые имеют обратные относительно операции умножения, множество R в данном случае ...
... a = bq1 + r1 , b = r1 q2 + r2 , r1 = r2 q3 + r3 , . . . . . . . . . . . . . rn-2 = rn-1qn-1+ rn . Докажем, что каждое из чисел rk линейно выражается через a и b с целыми коэффициентами. Для r1 утверждение тривиально: r1 = a - bq1 . Считая, что каждое из чисел r1 , r2 , . . . , rn-1 является целочисленной линейной комбинацией чисел a ...
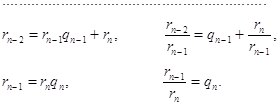
0 комментариев