Навигация
Ad=0. Возможно 8 случаев (см. предыдущий пункт)
4. ad=0. Возможно 8 случаев (см. предыдущий пункт).
bc=3. Возможно 2 случая (см. первый пункт).
Получили с данным условием 16 обратимых матриц.
Таким образом, по данной классификации получаем 8+8+16+16+16=48 обратимых матриц, определитель которых равен 1. Аналогичную классификацию можно составить для обратимых матриц с определителем равным 3, и число таких матриц будет также равно 48.
Следовательно, из 256 квадратных матриц второго порядка над Z4 обратимыми являются 96.
Обратимые матрицы над Z6.
| * | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 |
| 2 | 0 | 2 | 4 | 0 | 2 | 4 |
| 3 | 0 | 3 | 0 | 3 | 0 | 3 |
| 4 | 0 | 4 | 2 | 0 | 4 | 2 |
| 5 | 0 | 5 | 4 | 3 | 2 | 1 |
В Z6 обратимыми элементами являются 1 и 5. Аналогично рассмотрим, сколько обратимых матриц с определителем равным 1:
|A|=ad-bc=1.
Разобьем на следующие варианты:
1. ad=5. Возможные случаи:
1) a=1 Ù d=5,
2) a=5 Ù d=1,
bc=4. Возможные случаи:
1) b=1 Ù c=4,
2) b=4 Ù c=1,
3) b=2 Ù c=5,
4) b=5 Ù c=2,
5) b=c=2,
6) b=c=4.
Получили с данным условием 12 обратимых матриц.
2. ad=4. Возможно 6 случаев (см. предыдущий пункт).
bc=3. Возможные случаи:
1) b=3 Ù c=1,
2) b=1 Ù c=3,
3) b=3 Ù c=5,
4) b=5 Ù c=3,
5) b=c=3.
Получили с данным условием 30 обратимых матриц.
3. ad=3. Возможно 5 случаев (см. предыдущий пункт).
bc=2. Возможные случаи:
1) b=2 Ù c=1,
2) b=1 Ù c=2,
3) b=2 Ù c=4,
4) b=4 Ù c=2,
5) b=4 Ù c=5,
6) b=5 Ù c=4.
Получили с данным условием 30 обратимых матриц.
4. ad=2. Возможно 6 случаев (см. предыдущий пункт).
bc=1. Возможные случаи:
1) b=c=1,
2) b=c=5.
Получили с данным условием 12 обратимых матриц.
5. ad=1. Возможно 2 случая (см. предыдущий пункт).
bc=0. Возможные случаи:
1) b=0 Ù c=1,
2) b=0 Ù c=2,
3) b=0 Ù c=3,
4) b=0 Ù c=4,
5) b=0 Ù c=5,
6) b=1 Ù c=0,
7) b=2 Ù c=0,
8) b=3 Ù c=0,
9) b=4 Ù c=0,
10) b=5 Ù c=0,
11) b=2 Ù c=3,
12) b=3 Ù c=2,
13) b=3 Ù c=4,
14) b=4 Ù c=3,
15) b=c=0.
Получили с данным условием 30 обратимых матриц.
Похожие работы
... гомоморфизм . K= - подгруппа Z и значит K=mZ для некоторого целого m. Отсюда следует, что H= . При этом и потому n=dm где d - целое. По теореме о гомоморфизме . Из доказанных теорем следует, что всякая подгруппа циклической группы циклична. Мы видим также, что для каждого целого d, делящего порядок n конечной циклической группы имеется и притом ровно одна подгруппа порядка d, то есть для ...
... но они не равны друг другу. Так будет, например, для подкольца , состоящего из матриц с нулевой последней строкой и последним столбцом; =diag(1,1,...,1,0) =diag(1,1,...,1). Определение. Гомоморфизмом колец называется отображение, сохраняющее обе кольцевые операции: и . Изоморфизм - это взаимно однозначный гомоморфизм. Ядро гомоморфизма - это ядро группового гомоморфизма аддитивных групп , то ...
... -x * y. Полем называется такое ассоциативное коммутативное кольцо с единицей k, в котором всякий ненулевой элемент обратим: . Таким образом, по определению в поле отсутствуют делители нуля. Кольцом называется множество с двумя алгебраическими операциями R (+, *), если: 0. Обратимыми называют те элементы кольца R, которые имеют обратные относительно операции умножения, множество R в данном случае ...
... a = bq1 + r1 , b = r1 q2 + r2 , r1 = r2 q3 + r3 , . . . . . . . . . . . . . rn-2 = rn-1qn-1+ rn . Докажем, что каждое из чисел rk линейно выражается через a и b с целыми коэффициентами. Для r1 утверждение тривиально: r1 = a - bq1 . Считая, что каждое из чисел r1 , r2 , . . . , rn-1 является целочисленной линейной комбинацией чисел a ...
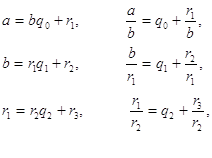
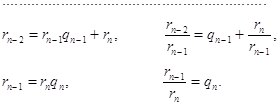
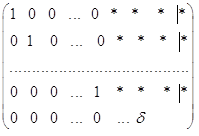
0 комментариев