Формула для подсчета обратимых матриц порядка 3

2. Формула для подсчета обратимых матриц порядка 3.

Будем рассматривать матрицы .

Алгебраические дополнения к элементам ,  и  есть определители матриц ,  и  соответственно, порядка 2, при чем 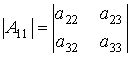,  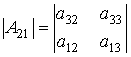и .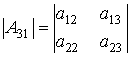

Нужно найти количество всех невырожденных матриц ().
 При этом

(2.1)

Формулу выведем в 3 этапа.

1)  Пусть  (р-1 штук),  (их количество по формуле (1.5)),  (по р штук) (2.2).

Тогда количество таких матриц вычисляется по формуле

(р-1)³р⁵(р+1) (2.3)

Мы утверждаем, что по этой же формуле вычисляется количество матриц, определитель которых не обращается в нуль, при условии, что , .

При условии (2.2) не учитываются матрицы вида  с неравным нулю определителем, количество которых нужно прибавить. Но сосчитали матрицы вида  с определителем обращающимся в нуль, количество которых нужно вычесть.

Докажем, что количество матриц в обоих случаях одинаково:

а)  (р-1 штук),  и . Из (2.1) получаем равенство .

а1) Пусть =0. Тогда  и . Значит элементов  всего р-1 штук, количество невырожденных матриц  - (р-1)²р(р+1). Т.к  то из выражения  получаем равенство , т.е. хотя бы один из этих элементов не равен нулю. Пусть . Из того, что  получаем . Элементом , принимающим любое значение, можем однозначно задать элемент . Поэтому количество матриц удовлетворяющих этим условиям (р-1)⁴×р²×(р+1) штук.

а2) Если ¹0, .Тогда  и . Значит элементов  всего р-1 штук, количество невырожденных матриц  - (р-1)²р(р+1). Т.к , то, из выражения  получаем . Пусть . Домножим равенство  () на . Заменим  на  (из того, что ). Получим равенство . Вынесем  за скобки  и т.к.  делаем вывод, что . Значит и  (). Поэтому количество матриц удовлетворяющих этим условиям (р-1)⁵×р×(р+1) штук.

а3) Если ¹0,  и  получаем (р-1)⁴×р²×(р+1) штук матриц удовлетворяющих этим условиям (рассуждение как в пункте а1)

а4) Если ¹0, ,  и  получаем
(р-1)⁵×р×(р+1) штук матриц удовлетворяющих этим условиям (рассуждение как в пункте а2)

а5) Если ¹0, ,  и . Из того, что  получаем . Пусть . Равенство  () умножим на  и заменим  на  (). Получим равенство . Вынося  за скобки (), замечаем, что элемент  однозначно выражается через  ( - р-1 штук). Но тогда  тоже выражается через эти элементы. Поэтому количество матриц удовлетворяющих этим условиям (р-1)⁶×р×(р+1)штук.

Таким образом, общее количество матриц удовлетворяющих условию пункта а) подсчитывается по формуле
(р-1)⁴×р×(р+1)×(р²+2р-1) (получается суммированием формул полученных в пунктах а1-а5).

б)  (р-1 штук),  ((р-1)²×р×(р+1)) штук). Т.к. , значит (2.4)

б1) Пусть =0. Тогда из (2.4) выводится равенство

(2.5)

а из (2.5) получим . Распишем (2.5): . Т.е.  однозначно выражается через элемент , которых может быть р штук, и через элементы , , , , . Поэтому количество матриц удовлетворяющих этим условиям (р-1)⁴×р²×(р+1).

б2) Если ¹0, .Тогда получим опять равенство (2.5) и из него . Элементов  всего р-1 штук. Т.к , то получаем что . Пусть . Умножив равенство (2.5) на , выражая  и произведя замену  на  получим равенство . А т.к.  и  делаем вывод, что  и  выражаются через все остальные элементы матрицы. Поэтому количество матриц удовлетворяющих этим условиям
(р-1)⁵×р×(р+1) штук.

б3) Если ¹0,  и  получаем (р-1)⁴×р²×(р+1) матриц удовлетворяющих этим условиям (рассуждения как в
пункте б1)

б4) Если ¹0, ,  и  получаем
(р-1)⁵×р×(р+1) матриц удовлетворяющих этим условиям (рассуждения как в пункте б2)

б5) Пусть ¹0, ,  и . Из того, что , получаем . Пусть . Тогда преобразовывая (2.4) получаем, что  однозначно выражается через  и все остальные элементы.

Поэтому количество матриц удовлетворяющих этим условиям (р-1)⁶×р×(р+1) штук.

Таким образом, общее количество матриц удовлетворяющих условию пункта б) подсчитывается по формуле
 (р-1)⁴×р×(р+1)×(р²+2р-1) (получается суммированием формул полученных в пунктах б1-б5).

Значит формула (р-1)³р⁵(р+1) для случая 1) при условии (2.2) верна.

2) Пусть ,  (количество их р-1),  (количество высчитывается по формуле (1.5)) и  (по р штук). Тогда из (2.1) получаем

.

Тогда количество таких матриц вычисляется по формуле

(р-1)³р⁴(р+1) (2.6)

Мы утверждаем, что по этой же формуле вычисляется количество матриц, определитель которых не обращается в нуль, при условии, что ,  и .

Но при этих условиях не учитываются матрицы вида  с неравным нулю определителем, количество которых нужно прибавить. Но сосчитали матрицы вида  с определителем обращающимся в нуль, количество которых нужно вычесть.

Докажем, что количество матриц в обоих случаях одинаково:

а) ,  и . Из (2.1) получаем равенство , , а из того что  получаем что, например, элемент  однозначно выражается через элемент  (р штук) и все остальные элементы. А значит количество матриц с данными условиями (р-1)⁴р²(р+1).

б) ,  и . Из (2.1) получаем равенство , . А из  можем однозначно выразить, например, элемент  через элемент  (р штук) и все остальные элементы. А значит количество матриц с данными условиями (р-1)⁴р²(р+1).

3) Пусть , ,  (количество их p-1),  (количество высчитывается по формуле (1.5)) и  (по р штук).

Тогда количество таких матриц вычисляется по формуле

(р-1)[(р-1)²р(р+1)]×р×р×р (2.7)

Этими этапами мы перебрали все случаи невырожденных матриц порядка 3. складывая формулы (2.3), (2.6) и (2.7), полученные в этапах 1), 2) и 3) получаем формулу для нахождения количества обратимых матриц порядка 3 матриц над полем Z_p

 

(р-1)³р³(р+1)(р²+р+1) (2.8)

 

3. Общая формула для подсчета обратимых матриц над полем Z_p.

Используя алгоритм, описанный в предыдущих пунктах, для выведения формулы подсчета количества обратимых матриц, можем получить частные формулы для матриц произвольных порядков.

Например:

Для матриц порядка 4:

(р-1)⁴р⁶(р+1)(р²+р+1)(р³+р²+р+1).

Для матриц порядка 5:

(р-1)⁵р¹⁰(р+1)(р²+р+1)(р³+р²+р+1)( р⁴+р³+р²+р+1), и т.д.

Анализируя полученные результаты, можем сделать выводы, что общая формула для получения количества обратимых матриц порядка n над полем Z_p выглядит так:

Данную формулу тождественными преобразованиями можно привести к виду:

 

§3. Обратимые матрицы над кольцом Z_n 

Из теоремы доказанной в § 1 следует, что для определителей матриц A и B выполняется равенство |A·B|=|A|·|B|.

Для обратимых матриц A и B следует A·B=E.Следовательно |A·B|=|A|·|B|=|E|=1.

Таким образом, получаем: определитель обратимой матрицы является обратимым элементом.

Попытаемся сосчитать количество обратимых матриц над некоторыми кольцами вычетов по составному модулю.

Обратимые матрицы над Z₄.

*	0	1	2	3
0	0	0	0	0
1	0	1	2	3
2	0	2	0	2
3	0	3	2	1

Всего различных матриц второго порядка над Z₄: 4⁴=256.

В Z₄ обратимыми элементами являются 1и3. Рассмотрим сколько обратимых матриц с определителем равным 1: |A|=ad-bc=1.

Разобьем на следующие варианты:

1. ad=3. Возможные случаи:

1)  a=1 Ù d=3,

2)  a=3 Ù d=1,

bc=2. Возможные случаи:

1)  b=1 Ù c=2,

2)  b=2 Ù c=1,

3)  b=2 Ù c=3,

4)  b=3 Ù c=2.

Получили с данным условием 8 обратимых матриц.

2. ad=2. Возможно 4 случая (см. предыдущий пункт).

bc=1. Возможные случаи:

1)  b=c=1,

2)  b=c=3.

Получили с данным условием 8 обратимых матриц.

3. ad=1. Возможно 2 случая (см. предыдущий пункт).

bc=0. Возможные случаи:

1)  b=0 Ù c=1,

2)  b=0 Ù c=2,

3)  b=0 Ù c=3,

4)  b=1 Ù c=0,

5)  b=2 Ù c=0,

6)  b=3 Ù c=0,

7)  b=c=0,

8)  b=c=2.

Получили сданным условием 16 обратимых матриц.