Навигация
Группировка статистических данных
2.2 Группировка статистических данных
Число групп определяется по формуле Стерджесса (2.2):
![]() , (2.2)
, (2.2)
где ![]() – количество групп;
– количество групп;
![]() – объем выборки.
– объем выборки.
После определения числа групп следует определить интервалы группировки - значения варьирующего признака, лежащие в определенных границах. Величина равного интервала определяется по формуле (2.3):
|
где ![]() – число групп интервалов,
– число групп интервалов,
![]() – размах выборки .
– размах выборки .
Ниже приведены значения числа групп интервалов для всех выборок:
При ![]() :
: ![]() .
.
При ![]() :
: ![]() .
.
При ![]() :
:![]() .
.
При ![]() :
:![]() .
.
При ![]() :
: ![]() .
.
При ![]() :
:![]() .
.
При ![]() :
:![]() .
.
При ![]() :
:![]() .
.
При ![]() :
: ![]() .
.
При ![]() :
: ![]() .
.
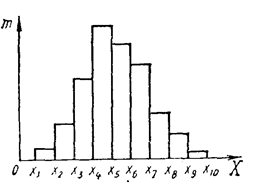
Построение интервального ряда в пакете STATISTICA производилось следующим образом:
а) Analysis→Frequency tables→Variables(выбрали переменную);
б) установили количество интервалов в “No. of exact intervals”, посчитанных по формуле Стерджесса;
в) установили флажки в Display options:
- Cumulative frequencies – накопленные частоты;
- Percentages - частости;
- Cumulative percentages – накопленные частости.
Интервальные ряды по каждой выборке для случайных величин X и Y приведены в таблицах 2.2-2.7 и Д.1-Д.14.
Таблица 2.2 - Интервальный ряд СВ ![]() при
при ![]()
| Частота | Кумул. частота | Процент | Кумул. процент | |
| 5,475289<x<=8,510050 | 8 | 8 | 8,00000 | 8,0000 |
| 8,510050<x<=11,54481 | 15 | 23 | 15,00000 | 23,0000 |
| 11,54481<x<=14,57957 | 16 | 39 | 16,00000 | 39,0000 |
| 14,57957<x<=17,61433 | 18 | 57 | 18,00000 | 57,0000 |
| 17,61433<x<=20,64909 | 20 | 77 | 20,00000 | 77,0000 |
| 20,64909<x<=23,68385 | 13 | 90 | 13,00000 | 90,0000 |
| 23,68385<x<=26,71862 | 10 | 100 | 10,00000 | 100,0000 |
Таблица 2.3 - Интервальный ряд СВ ![]() при
при ![]()
| Частота | Кумул. частота | Процент | Кумул. процент | |
| 5,850935<x<=8,116734 | 25 | 25 | 5,00000 | 5,0000 |
| 8,116734<x<=10,38253 | 62 | 87 | 12,40000 | 17,4000 |
| 10,38253<x<=12,64833 | 64 | 151 | 12,80000 | 30,2000 |
| 12,64833<x<=14,91413 | 55 | 206 | 11,00000 | 41,2000 |
| 14,91413<x<=17,17993 | 70 | 276 | 14,00000 | 55,2000 |
| 17,17993<x<=19,44573 | 64 | 340 | 12,80000 | 68,0000 |
| 19,44573<x<=21,71153 | 74 | 414 | 14,80000 | 82,8000 |
| 21,71153<x<=23,97733 | 59 | 473 | 11,80000 | 94,6000 |
| 23,97733<x<=26,24313 | 27 | 500 | 5,40000 | 100,0000 |
Таблица 2.4 - Интервальный ряд СВ ![]() при
при ![]()
| Частота | Кумул. частота | Процент | Кумул. процент | |
| 5,745344<x<=7,797069 | 50 | 50 | 5,00000 | 5,0000 |
| 7,797069<x<=9,848795 | 106 | 156 | 10,60000 | 15,6000 |
| 9,848795<x<=11,90052 | 134 | 290 | 13,40000 | 29,0000 |
| 11,90052<x<=13,95225 | 88 | 378 | 8,80000 | 37,8000 |
| 13,95225<x<=16,00397 | 117 | 495 | 11,70000 | 49,5000 |
| 16,00397<x<=18,05570 | 121 | 616 | 12,10000 | 61,6000 |
| 18,05570<x<=20,10742 | 107 | 723 | 10,70000 | 72,3000 |
| 20,10742<x<=22,15915 | 117 | 840 | 11,70000 | 84,0000 |
| 22,15915<x<=24,21087 | 111 | 951 | 11,10000 | 95,1000 |
| 24,21087<x<=26,26260 | 49 | 1000 | 4,90000 | 100,0000 |
Таблица 2.5 - Интервальный ряд СВ ![]() при
при ![]()
| Частота | Кумул. | Процент | Кумул. | |
| 0,231076<x<=4,627075 | 1 | 1 | 1,00000 | 1,0000 |
| 4,627075<x<=9,023072 | 6 | 7 | 6,00000 | 7,0000 |
| 9,023072<x<=13,41907 | 20 | 27 | 20,00000 | 27,0000 |
| 13,41907<x<=17,81507 | 31 | 58 | 31,00000 | 58,0000 |
| 17,81507<x<=22,21107 | 22 | 80 | 22,00000 | 80,0000 |
| 22,21107<x<=26,60706 | 17 | 97 | 17,00000 | 97,0000 |
| 26,60706<x<=31,00306 | 3 | 100 | 3,00000 | 100,0000 |
Таблица 2.6 - Интервальный ряд СВ ![]() при
при ![]()
| Частота | Кумул. | Процент | Кумул. | |
| -1,89766<x<=2,289667 | 2 | 2 | 0,40000 | 0,4000 |
| 2,289667<x<=6,476997 | 21 | 23 | 4,20000 | 4,6000 |
| 6,476997<x<=10,66433 | 59 | 82 | 11,80000 | 16,4000 |
| 10,66433<x<=14,85166 | 125 | 207 | 25,00000 | 41,4000 |
| 14,85166<x<=19,03899 | 147 | 354 | 29,40000 | 70,8000 |
| 19,03899<x<=23,22632 | 99 | 453 | 19,80000 | 90,6000 |
| 23,22632<x<=27,41365 | 39 | 492 | 7,80000 | 98,4000 |
| 27,41365<x<=31,60098 | 7 | 499 | 1,40000 | 99,8000 |
Таблица 2.7 - Интервальный ряд СВ ![]() при
при ![]()
| Частота | Кумул. | Процент | Кумул. | |
| -3,54794<x<=0,400491 | 5 | 5 | 0,50000 | 0,5000 |
| 0,400491<x<=4,348925 | 9 | 14 | 0,90000 | 1,4000 |
| 4,348925<x<=8,297359 | 61 | 75 | 6,10000 | 7,5000 |
| 8,297359<x<=12,24579 | 177 | 252 | 17,70000 | 25,2000 |
| 12,24579<x<=16,19423 | 279 | 531 | 27,90000 | 53,1000 |
| 16,19423<x<=20,14266 | 267 | 798 | 26,70000 | 79,8000 |
| 20,14266<x<=24,09110 | 154 | 952 | 15,40000 | 95,2000 |
| 24,09110<x<=28,03953 | 38 | 990 | 3,80000 | 99,0000 |
| 28,03953<x<=31,98797 | 8 | 998 | 0,80000 | 99,8000 |
| 31,98797<x<=35,93640 | 2 | 1000 | 0,20000 | 100,0000 |
Похожие работы
... отпуска может быть на 10–20оС ниже, а его продолжительность на 20–25% меньше, чем первого отпуска. Охлаждение после отпуска проводится на воздухе. 1.1.5 Влияние термической обработки на свойства штамповых сталей Служебные свойства штампового инструмента и его стойкость в значительной степени определяются соответствующим назначением марки стали, ее термообработкой и условиями эксплуатации ...
... о начавшихся в них процессах деградации, которые в дальнейшем приведут к условным отказам. В этом случае выбросы являются закономерными, обусловлены физическими процессами и их нельзя исключать из дальнейшего рассмотрения при статистической обработке результатов испытаний. Поэтому для принятия того или иного решения проводят тщательный комплексный анализ возможных причин указанных отклонений. ...
... в процессе обучения, необходима разработка совершенно новых подходов к работе с таким видом информационных ресурсов как базы данных. Глава 2.Технология использования баз данных математических задач в процессе подготовки учащихся к ЕГЭ по математике 2.1 Реализация модели В соответствии с теорией поэтапного формирования умственных действий учащихся, подготовку к сдаче единого ...
... плана ФЭ. Большое разнообразие моделей РК приводит к необходимости использования разнообразных способов и технических средств для измерения их параметров. Как правило, статические и динамические параметры РК измеряют на разных технологических установках. Методы построения средств измерения для идентификации моделей РК могут быть сведены к следующим принципам, учитывающим особенности подключения ...

0 комментариев