Навигация
Графическое изображение рядов распределения
2.3 Графическое изображение рядов распределения
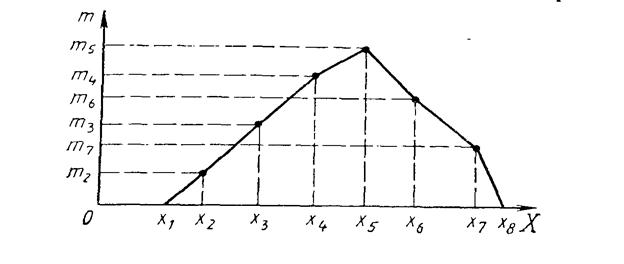
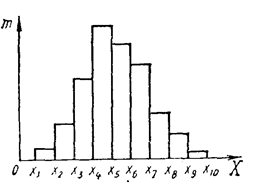
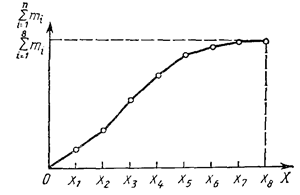
Графическое изображение интервальных рядов включает построения полигона частот, гистограммы и кумуляты.
В пакете STATISTICA построение полигона происходит следующим образом:
а) Analysis → Frequency tables → Variables (выбрать переменную);
б) установить количество интервалов в “No. of exact intervals”;
в) Frequency tables → Count;
г) нажать правую кнопку мыши и из выпадающего списка выбрать “Custom Graphs”;
д) 2D Graphs → Graph Type → Line Plot. [1]
Построение кумуляты:
а)Analysis → Frequency tables → Variables (выбрать переменную);
б) установить количество интервалов в “No. of exact intervals”;
в) Frequency tables → Cumul. Count;
г) нажать правую кнопку мыши и выбрать “Custom Graphs”;
д) 2D Graphs → Graph Type → Line Plot (Bar ![]() ).
).
Построение гистограммы происходит следующим образом:
а) Analysis → Frequency tables → Variables (выбрать переменную);
б) установить количество интервалов в “No. of exact intervals”;
в) Frequency tables → Percent;
г) нажать правую кнопку мыши и из выпадающего списка выбрать “Custom Graphs”;
д) 2D Graphs → Graph Type → Bar ![]()
2.4 Точечные оценки средних показателей
Точечная оценка математического ожидания по вариационному ряду вычисляется по формуле (2.4):
|
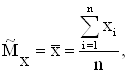
где ![]() – значения элементов выборки.
– значения элементов выборки.
Оценка дисперсии по вариационному ряду вычисляется по формуле (2.5).
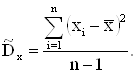
|
Вычисление оценки математического ожидания по интервальному вариационному ряду осуществляется по формуле (2.6):
|
где ![]() – середина
– середина ![]() -го интервала;
-го интервала;
![]() – статистическая вероятность (частость) попадания в
– статистическая вероятность (частость) попадания в ![]() -тый интервал.
-тый интервал.
Оценка дисперсии для интервального ряда вычисляется по формуле (2.7):
|

Вычисление точечных оценок по вариационному ряду в пакете STATISTICA:
Analysis → Descriptive statistics → Categorization → Number of intervals (установить количество интервалов) → More statistics → Mean, Variance. [2]
Значения точечных оценок математического ожидания и дисперсии для простого и интервального рядов приведены в таблице 2.8.
Таблица 2.8 – Оценки математического ожидания и дисперсии
| Выборка | Математическое ожидание | Дисперсия | ||
| Простой ряд | Интервальный ряд | Простой ряд | Интервальный ряд | |
|
| 16,254 | 16,279 | 27,849 | 28,517 |
|
| 16,189 | 16,174 | 26,259 | 26,598 |
|
| 15,950 | 16,006 | 27,608 | 28,330 |
|
| 16,668 | 16,936 | 31,125 | 31,113 |
|
| 15,989 | 16,007 | 30,406 | 31,242 |
|
| 15,792 | 15,740 | 27,059 | 28,636 |
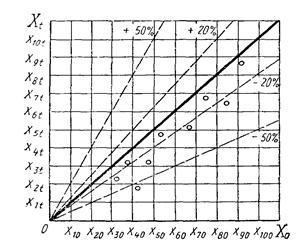
Из приведенных данных видно, что полученные оценки математического ожидания и дисперсии по вариационному (простому) и интервальному рядам имеют близкие значения. Причем, чем больше объем выборки, тем более точный результат. От номера эксперимента, то есть от количества испытаний величины точечной оценки не зависят. Это видно на рисунках 2.25 – 2.32.
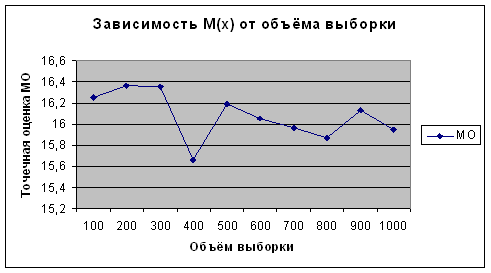
Рисунок 2.25 - Зависимость ![]() от объема выборки для
от объема выборки для ![]()
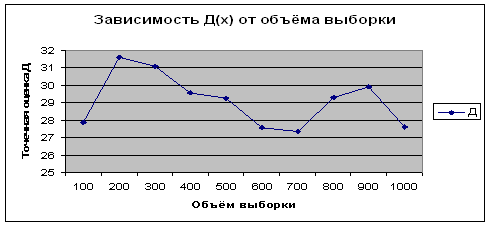
Рисунок 2.26 - Зависимость ![]() от объема выборки для
от объема выборки для ![]()
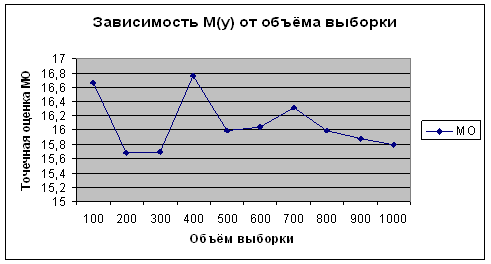
Рисунок 2.27 - Зависимость ![]() от объема выборки для
от объема выборки для ![]()
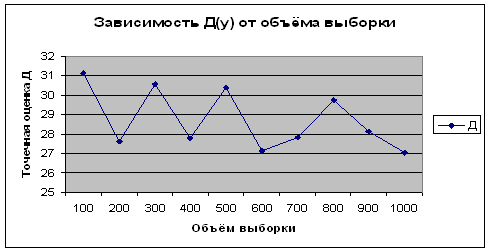
Рисунок 2.28 - Зависимость ![]() от объема выборки для
от объема выборки для ![]()
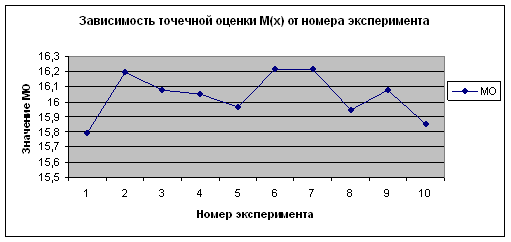
Рисунок 2.29 - Зависимость ![]() от номера эксперимента по
от номера эксперимента по ![]()

Рисунок 2.30 - Зависимость ![]() от номера эксперимента по
от номера эксперимента по ![]()
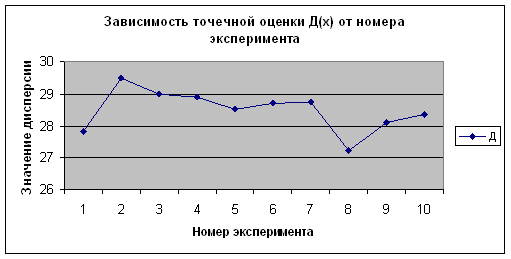
Рисунок 2.31 - Зависимость ![]() от номера эксперимента по
от номера эксперимента по ![]()
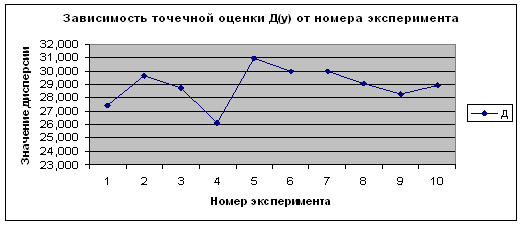
Рисунок 2.32 - Зависимость ![]() от номера эксперимента по
от номера эксперимента по ![]()
В таблице 2.9 приведены оценки математического ожидания и дисперсии, вычисленные для 10 выборок по 1000 элементов в каждой для случайной величины ![]() и случайной величины
и случайной величины ![]() .
.
Таблица 2.9 – Точечные оценки выборок из 1000 элементов для ![]() и
и ![]()
|
|
| |||
| Выборка |
|
|
|
|
| 1 | 15,792 | 27,832 | 15,754 | 27,421 |
| 2 | 16,193 | 29,501 | 16,283 | 29,650 |
| 3 | 16,076 | 29,006 | 15,900 | 28,716 |
| 4 | 16,052 | 28,884 | 16,096 | 26,124 |
| 5 | 15,968 | 28,508 | 15,947 | 30,983 |
| 6 | 16,212 | 28,710 | 16,163 | 29,956 |
| 7 | 16,215 | 28,747 | 16,030 | 30,011 |
| 8 | 15,945 | 27,243 | 16,428 | 29,069 |
| 9 | 16,080 | 28,103 | 16,054 | 28,265 |
| 10 | 15,853 | 28,369 | 15,980 | 28,913 |
Похожие работы
... отпуска может быть на 10–20оС ниже, а его продолжительность на 20–25% меньше, чем первого отпуска. Охлаждение после отпуска проводится на воздухе. 1.1.5 Влияние термической обработки на свойства штамповых сталей Служебные свойства штампового инструмента и его стойкость в значительной степени определяются соответствующим назначением марки стали, ее термообработкой и условиями эксплуатации ...
... о начавшихся в них процессах деградации, которые в дальнейшем приведут к условным отказам. В этом случае выбросы являются закономерными, обусловлены физическими процессами и их нельзя исключать из дальнейшего рассмотрения при статистической обработке результатов испытаний. Поэтому для принятия того или иного решения проводят тщательный комплексный анализ возможных причин указанных отклонений. ...
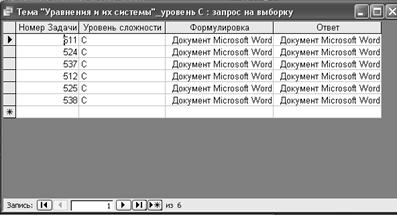
... в процессе обучения, необходима разработка совершенно новых подходов к работе с таким видом информационных ресурсов как базы данных. Глава 2.Технология использования баз данных математических задач в процессе подготовки учащихся к ЕГЭ по математике 2.1 Реализация модели В соответствии с теорией поэтапного формирования умственных действий учащихся, подготовку к сдаче единого ...
... плана ФЭ. Большое разнообразие моделей РК приводит к необходимости использования разнообразных способов и технических средств для измерения их параметров. Как правило, статические и динамические параметры РК измеряют на разных технологических установках. Методы построения средств измерения для идентификации моделей РК могут быть сведены к следующим принципам, учитывающим особенности подключения ...

0 комментариев