Навигация
Проверка нормальности эмпирического распределения на основе критериев согласия Пирсона
2.10 Проверка нормальности эмпирического распределения на основе критериев согласия Пирсона
Для проверки гипотезы о соответствии эмпирического распределения нормальному закону распределения необходимо ввести нулевую гипотезу, которая будет проверяться по критерию Пирсона.
![]() : генеральная совокупность распределена по нормальному закону.
: генеральная совокупность распределена по нормальному закону.
В качестве меры расхождения для критерия ![]() выбирается величина, равная взвешенной сумме квадратов отклонений статистической вероятности от соответствующей теоретической вероятности, рассчитанных по нормальному закону теоретического распределения
выбирается величина, равная взвешенной сумме квадратов отклонений статистической вероятности от соответствующей теоретической вероятности, рассчитанных по нормальному закону теоретического распределения ![]() вычисляется по формуле (2.20)
вычисляется по формуле (2.20)
|
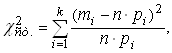
где ![]() – частота попадания в i-тый интервал;
– частота попадания в i-тый интервал;
![]() – объем выборки;
– объем выборки;
![]() – теоретическая вероятность попадания i-тый интервал:
– теоретическая вероятность попадания i-тый интервал:

|
Общая схема применения критерия ![]() :
:
1. Определение меры расхождения по формуле 2.20;
2. Задание уровня значимости ![]() ;
;
3. Определение числа степеней свободы ![]() по формуле 2.22.
по формуле 2.22.
![]() , (2.22)
, (2.22)
где ![]() – количество интервалов в интервальном ряду;
– количество интервалов в интервальном ряду;
![]() – число налагаемых связей, равное числу параметров
– число налагаемых связей, равное числу параметров
предполагаемого закона распределения
4. Область принятия основной гипотезы:
![]() .
.
Выполнение в пакете STATISTICA.
В модуле Nonparametric Statistics (непараметрическая статистика), Distribution Fitting. В поле Continuous Distributions представлены непрерывные распределения, а в поле Discrete Distributions - дискретные распределения (закон распределения выбираем дважды щелкнув на его название мышью) ® Variable (выбрать переменную) ® в поле Plot distribution выбираем Frequency distribution (частоты распределения) ® в поле Kolmogorov-Smirnov test ставим No → установим необходимые параметры числа интервалов, верхней и нижней границ, среднего и дисперсии → Graph. Результаты проверки соответствия гипотезы приведены в таблице 2.39 и показаны на рисунках 2.41-2.46
Таблица 2.39 – Значения ![]() и χ2крит для случайных величин
и χ2крит для случайных величин ![]() и
и ![]()
| Выборка |
|
|
| Гипотеза |
|
| 4 | 9,49 | 7,53 | Принимается |
|
| 4 | 9,49 | 11,815 | Отвергается |
|
| 5 | 11,1 | 11,95 | Отвергается |
|
| 5 | 11,1 | 25,54 | Отвергается |
|
| 6 | 12,59 | 45,51 | Отвергается |
|
| 6 | 12,59 | 39,83 | Отвергается |
|
| 6 | 12,59 | 48,77 | Отвергается |
|
| 7 | 14,1 | 40,81 | Отвергается |
|
| 7 | 14,1 | 49,97 | Отвергается |
|
| 7 | 14,1 | 76,75 | Отвергается |
|
| 4 | 9,49 | 2,04 | Принимается |
|
| 4 | 9,49 | 2,12 | Принимается |
|
| 5 | 11,1 | 2,78 | Принимается |
|
| 5 | 11,1 | 2,99 | Принимается. |
|
| 6 | 12,59 | 3,15 | Принимается |
|
| 6 | 12,59 | 4,61 | Принимается |
|
| 6 | 12,59 | 5,07 | Принимается |
|
| 7 | 14,1 | 5,86 | Принимается |
|
| 7 | 14,1 | 6,32 | Принимается |
|
| 7 | 14,1 | 7,16 | Принимается |
На основе полученных данных можно сделать вывод, что случайная величина ![]() распределена по нормальному закону, а случайная величина
распределена по нормальному закону, а случайная величина ![]() не распределена по нормальному закону.
не распределена по нормальному закону.
Анализируя получившиеся графики, делаем вывод, что случайная величина ![]() распределена по равномерному закону, а случайная величина
распределена по равномерному закону, а случайная величина ![]() – по нормальному.
– по нормальному.
Заключение
В ходе курсовой работы были освоены методы обработки данных статистического наблюдения, их анализа с помощью обобщающих показателей, установление теоретических законов распределения случайных величин и доказательство адекватности этих законов. Также в результате выполнения данной работы мы приобрели навыки и опыт работы в пакете STATISTICА.
В ходе анализа данных, были сделаны выводы, что основной частью статистического анализа является выявление закона распределения случайной величины, а также, выявление основных факторов, оказывающих влияние на качество оцениваемых параметров закона распределения (длина выборки, её однородность, величина доверительной вероятности). Был произведен статистический анализ каждой из полученных в ходе генерации выборок данных двух случайных величин, был найден закон их распределения. Рассмотрены основные числовые характеристики положения и вариации нормального и равномерного закона.
Полученный опыт работы со статистическими данными и методами их обработки на компьютере позволит гораздо быстрее и эффективнее применять эти методы обработки информации в повседневной жизни, в частности, для экономических исследований и разработок.
Перечень ссылок
случайный величина интервальный выборка
1. Теория статистики: Учебник / Под ред. проф. Р. А. Шмойловой. - 3-е изд., перераб. -М.: Финансы и статистика, 2000. - 560 с.
2. Елисеева И. И., Юзбашев М. М. Общая теория статистики: Учебник / Под ред. чл.-корр. РАН И. И. Елисеевой. – М.: Финансы и статистика, 1998. – 365 с.: ил.
3. Смирнов Н.В., Дунин-Барковский И.В. Курс теории вероятностей и математической статистики для технических приложений. – М.: Наука, 1969. – 509 с.
4. Гурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для втузов. Изд. 5-е перераб. и доп. – М.: Высш. школа, 1977. – 397 с.
5. Кремер Н.Ш. Теория вероятностей и математическая статистика. – М.: Unity, 2000. – 544 с.
6. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1969. – 576 с.
7. Боровиков В. STATISTICA: искусство анализа данных на компьютере. Для профессионалов. - СПб.: Питер, 2001. - 656 с.
Приложение А
Генерация исходных данных СВ ![]() в пакете STATISTICA
в пакете STATISTICA
Dim ADS As Spreadsheet
Dim STBReport As Report
Dim SUM As Double
Dim LOOP_CASE As Double
Dim I As Double
Sub Main
Set ADS = ActiveDataSet
Set STBReport = Reports.New
For LOOP_CASE = 1 To NCASES(ADS)
For I = 1 To n
SUM = 0
For L = 1 To 300
SUM = SUM + Uniform(1)
Next L
ADS.Value (LOOP_CASE, 1) = N * ((1 / 15) * SUM - 9)
Next I
NEXT_CASE:
Next LOOP_CASE
End Sub
Приложение Б
Интервальные ряды для СВ ![]() и
и ![]()
Таблица Д.1 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| 5,289175<x<=8,355050 | 14,000 | 14,000 | 7,000 | 7,000 |
| 8,355050<x<=11,42093 | 34,000 | 48,000 | 17,000 | 24,000 |
| 11,42093<x<=14,48680 | 33,000 | 81,000 | 16,500 | 40,500 |
| 14,48680<x<=17,55268 | 33,000 | 114,000 | 16,500 | 57,000 |
| 17,55268<x<=20,61855 | 29,000 | 143,000 | 14,500 | 71,500 |
| 20,61855<x<=23,68443 | 23,000 | 166,000 | 11,500 | 83,000 |
| 23,68443<x<=26,75030 | 34,000 | 200,000 | 17,000 | 100,000 |
Таблица Д.2 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| 5,502861<x<=8,114160 | 25,000 | 25,000 | 8,333 | 8,333 |
| 8,114160<x<=10,72546 | 37,000 | 62,000 | 12,333 | 20,667 |
| 10,72546<x<=13,33676 | 40,000 | 102,000 | 13,333 | 34,000 |
| 13,33676<x<=15,94806 | 39,000 | 141,000 | 13,000 | 47,000 |
| 15,94806<x<=18,55936 | 39,000 | 180,000 | 13,000 | 60,000 |
| 18,55936<x<=21,17066 | 41,000 | 221,000 | 13,667 | 73,667 |
| 21,17066<x<=23,78195 | 51,000 | 272,000 | 17,000 | 90,667 |
| 23,78195<x<=26,39325 | 28,000 | 300,000 | 9,333 | 100,000 |
Таблица Д.3 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| 5,555859<x<=8,176674 | 33,000 | 33,000 | 8,250 | 8,250 |
| 8,176674<x<=10,79749 | 69,000 | 102,000 | 17,250 | 25,500 |
| 10,79749<x<=13,41830 | 54,000 | 156,000 | 13,500 | 39,000 |
| 13,41830<x<=16,03912 | 54,000 | 210,000 | 13,500 | 52,500 |
| 16,03912<x<=18,65993 | 51,000 | 261,000 | 12,750 | 65,250 |
| 18,65993<x<=21,28075 | 58,000 | 319,000 | 14,500 | 79,750 |
| 21,28075<x<=23,90156 | 54,000 | 373,000 | 13,500 | 93,250 |
| 23,90156<x<=26,52238 | 27,000 | 400,000 | 6,750 | 100,000 |
Таблица Д.4 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| 5,616825<x<=7,918099 | 42,000 | 42,000 | 7,000 | 7,000 |
| 7,918099<x<=10,21937 | 60,000 | 102,000 | 10,000 | 17,000 |
| 10,21937<x<=12,52065 | 79,000 | 181,000 | 13,167 | 30,167 |
| 12,52065<x<=14,82192 | 78,000 | 259,000 | 13,000 | 43,167 |
| 14,82192<x<=17,12319 | 75,000 | 334,000 | 12,500 | 55,667 |
| 17,12319<x<=19,42447 | 69,000 | 403,000 | 11,500 | 67,167 |
| 19,42447<x<=21,72574 | 92,000 | 495,000 | 15,333 | 82,500 |
| 21,72574<x<=24,02701 | 70,000 | 565,000 | 11,667 | 94,167 |
| 24,02701<x<=26,32829 | 35,000 | 600,000 | 5,833 | 100,000 |
Таблица Д.5 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| 5,638499<x<=7,943963 | 48,000 | 48,000 | 6,857 | 6,857 |
| 7,943963<x<=10,24943 | 80,000 | 128,000 | 11,429 | 18,286 |
| 10,24943<x<=12,55489 | 80,000 | 208,000 | 11,429 | 29,714 |
| 12,55489<x<=14,86035 | 100,000 | 308,000 | 14,286 | 44,000 |
| 14,86035<x<=17,16582 | 91,000 | 399,000 | 13,000 | 57,000 |
| 17,16582<x<=19,47128 | 83,000 | 482,000 | 11,857 | 68,857 |
| 19,47128<x<=21,77675 | 94,000 | 576,000 | 13,429 | 82,286 |
| 21,77675<x<=24,08221 | 89,000 | 665,000 | 12,714 | 95,000 |
| 24,08221<x<=26,38767 | 35,000 | 700,000 | 5,000 | 100,000 |
Таблица Д.6 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| 5,746050<x<=7,794074 | 50,000 | 50,000 | 6,250 | 6,250 |
| 7,794074<x<=9,842099 | 87,000 | 137,000 | 10,875 | 17,125 |
| 9,842099<x<=11,89012 | 88,000 | 225,000 | 11,000 | 28,125 |
| 11,89012<x<=13,93815 | 110,000 | 335,000 | 13,750 | 41,875 |
| 13,93815<x<=15,98617 | 77,000 | 412,000 | 9,625 | 51,500 |
| 15,98617<x<=18,03420 | 84,000 | 496,000 | 10,500 | 62,000 |
| 18,03420<x<=20,08222 | 83,000 | 579,000 | 10,375 | 72,375 |
| 20,08222<x<=22,13025 | 77,000 | 656,000 | 9,625 | 82,000 |
| 22,13025<x<=24,17827 | 96,000 | 752,000 | 12,000 | 94,000 |
| 24,17827<x<=26,22630 | 48,000 | 800,000 | 6,000 | 100,000 |
Таблица Д.7 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| 5,747041<x<=7,795948 | 46,000 | 46,000 | 5,111 | 5,111 |
| 7,795948<x<=9,844855 | 118,000 | 164,000 | 13,111 | 18,222 |
| 9,844855<x<=11,89376 | 93,000 | 257,000 | 10,333 | 28,556 |
| 11,89376<x<=13,94267 | 84,000 | 341,000 | 9,333 | 37,889 |
| 13,94267<x<=15,99158 | 107,000 | 448,000 | 11,889 | 49,778 |
| 15,99158<x<=18,04048 | 85,000 | 533,000 | 9,444 | 59,222 |
| 18,04048<x<=20,08939 | 108,000 | 641,000 | 12,000 | 71,222 |
| 20,08939<x<=22,13830 | 88,000 | 729,000 | 9,778 | 81,000 |
| 22,13830<x<=24,18720 | 108,000 | 837,000 | 12,000 | 93,000 |
| 24,18720<x<=26,23611 | 63,000 | 900,000 | 7,000 | 100,000 |
Таблица Д.8 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| -3,85839<x<=1,661475 | 2,000 | 2,000 | 1,000 | 1,000 |
| 1,661475<x<=7,181336 | 7,000 | 9,000 | 3,500 | 4,500 |
| 7,181336<x<=12,70120 | 47,000 | 56,000 | 23,500 | 28,000 |
| 12,70120<x<=18,22106 | 79,000 | 135,000 | 39,500 | 67,500 |
| 18,22106<x<=23,74092 | 54,000 | 189,000 | 27,000 | 94,500 |
| 23,74092<x<=29,26078 | 8,000 | 197,000 | 4,000 | 98,500 |
| 29,26078<x<=34,78064 | 3,000 | 200,000 | 1,500 | 100,000 |
Таблица Д.9 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| -3,50252<x<=1,766314 | 2,000 | 2,000 | 0,667 | 0,667 |
| 1,766314<x<=7,035144 | 13,000 | 15,000 | 4,333 | 5,000 |
| 7,035144<x<=12,30397 | 63,000 | 78,000 | 21,000 | 26,000 |
| 12,30397<x<=17,57280 | 106,000 | 184,000 | 35,333 | 61,333 |
| 17,57280<x<=22,84163 | 91,000 | 275,000 | 30,333 | 91,667 |
| 22,84163<x<=28,11046 | 21,000 | 296,000 | 7,000 | 98,667 |
| 28,11046<x<=33,37929 | 3,000 | 299,000 | 1,000 | 99,667 |
| 33,37929<x<=38,64812 | 1,000 | 300,000 | 0,333 | 100,000 |
Таблица Д.10 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| 1,299935<x<=5,325310 | 5,000 | 5,000 | 1,250 | 1,250 |
| 5,325310<x<=9,350685 | 31,000 | 36,000 | 7,750 | 9,000 |
| 9,350685<x<=13,37606 | 63,000 | 99,000 | 15,750 | 24,750 |
| 13,37606<x<=17,40143 | 117,000 | 216,000 | 29,250 | 54,000 |
| 17,40143<x<=21,42681 | 109,000 | 325,000 | 27,250 | 81,250 |
| 21,42681<x<=25,45218 | 55,000 | 380,000 | 13,750 | 95,000 |
| 25,45218<x<=29,47756 | 16,000 | 396,000 | 4,000 | 99,000 |
| 29,47756<x<=33,50293 | 4,000 | 400,000 | 1,000 | 100,000 |
Таблица Д.11 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| -1,98797<x<=1,772650 | 1,000 | 1,000 | 0,167 | 0,167 |
| 1,772650<x<=5,533271 | 12,000 | 13,000 | 2,000 | 2,167 |
| 5,533271<x<=9,293892 | 54,000 | 67,000 | 9,000 | 11,167 |
| 9,293892<x<=13,05451 | 100,000 | 167,000 | 16,667 | 27,833 |
| 13,05451<x<=16,81513 | 166,000 | 333,000 | 27,667 | 55,500 |
| 16,81513<x<=20,57576 | 154,000 | 487,000 | 25,667 | 81,167 |
| 20,57576<x<=24,33638 | 88,000 | 575,000 | 14,667 | 95,833 |
| 24,33638<x<=28,09700 | 17,000 | 592,000 | 2,833 | 98,667 |
| 28,09700<x<=31,85762 | 8,000 | 600,000 | 1,333 | 100,000 |
Таблица Д.12 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| -2,68355<x<=1,245110 | 2,000 | 2,000 | 0,286 | 0,286 |
| 1,245110<x<=5,173768 | 10,000 | 12,000 | 1,429 | 1,714 |
| 5,173768<x<=9,102425 | 41,000 | 53,000 | 5,857 | 7,571 |
| 9,102425<x<=13,03108 | 149,000 | 202,000 | 21,286 | 28,857 |
| 13,03108<x<=16,95974 | 180,000 | 382,000 | 25,714 | 54,571 |
| 16,95974<x<=20,88840 | 178,000 | 560,000 | 25,429 | 80,000 |
| 20,88840<x<=24,81705 | 102,000 | 662,000 | 14,571 | 94,571 |
| 24,81705<x<=28,74571 | 31,000 | 693,000 | 4,429 | 99,000 |
| 28,74571<x<=32,67437 | 7,000 | 700,000 | 1,000 | 100,000 |
Таблица Д.13 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| -1,52038<x<=2,421483 | 4,000 | 4,000 | 0,500 | 0,500 |
| 2,421483<x<=6,363342 | 37,000 | 41,000 | 4,625 | 5,125 |
| 6,363342<x<=10,30520 | 69,000 | 110,000 | 8,625 | 13,750 |
| 10,30520<x<=14,24706 | 185,000 | 295,000 | 23,125 | 36,875 |
| 14,24706<x<=18,18892 | 231,000 | 526,000 | 28,875 | 65,750 |
| 18,18892<x<=22,13078 | 175,000 | 701,000 | 21,875 | 87,625 |
| 22,13078<x<=26,07264 | 75,000 | 776,000 | 9,375 | 97,000 |
| 26,07264<x<=30,01449 | 20,000 | 796,000 | 2,500 | 99,500 |
| 30,01449<x<=33,95635 | 3,000 | 799,000 | 0,375 | 99,875 |
| 33,95635<x<=37,89821 | 1,000 | 800,000 | 0,125 | 100,000 |
Таблица Д.14 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| -1,06170<x<=2,578305 | 3,000 | 3,000 | 0,333 | 0,333 |
| 2,578305<x<=6,218309 | 36,000 | 39,000 | 4,000 | 4,333 |
| 6,218309<x<=9,858313 | 71,000 | 110,000 | 7,889 | 12,222 |
| 9,858313<x<=13,49832 | 171,000 | 281,000 | 19,000 | 31,222 |
| 13,49832<x<=17,13832 | 277,000 | 558,000 | 30,778 | 62,000 |
| 17,13832<x<=20,77832 | 176,000 | 734,000 | 19,556 | 81,556 |
| 20,77832<x<=24,41833 | 110,000 | 844,000 | 12,222 | 93,778 |
| 24,41833<x<=28,05833 | 47,000 | 891,000 | 5,222 | 99,000 |
| 28,05833<x<=31,69833 | 7,000 | 898,000 | 0,778 | 99,778 |
| 31,69833<x<=35,33834 | 2,000 | 900,000 | 0,222 | 100,000 |
Похожие работы
... отпуска может быть на 10–20оС ниже, а его продолжительность на 20–25% меньше, чем первого отпуска. Охлаждение после отпуска проводится на воздухе. 1.1.5 Влияние термической обработки на свойства штамповых сталей Служебные свойства штампового инструмента и его стойкость в значительной степени определяются соответствующим назначением марки стали, ее термообработкой и условиями эксплуатации ...
... о начавшихся в них процессах деградации, которые в дальнейшем приведут к условным отказам. В этом случае выбросы являются закономерными, обусловлены физическими процессами и их нельзя исключать из дальнейшего рассмотрения при статистической обработке результатов испытаний. Поэтому для принятия того или иного решения проводят тщательный комплексный анализ возможных причин указанных отклонений. ...
... в процессе обучения, необходима разработка совершенно новых подходов к работе с таким видом информационных ресурсов как базы данных. Глава 2.Технология использования баз данных математических задач в процессе подготовки учащихся к ЕГЭ по математике 2.1 Реализация модели В соответствии с теорией поэтапного формирования умственных действий учащихся, подготовку к сдаче единого ...
... плана ФЭ. Большое разнообразие моделей РК приводит к необходимости использования разнообразных способов и технических средств для измерения их параметров. Как правило, статические и динамические параметры РК измеряют на разных технологических установках. Методы построения средств измерения для идентификации моделей РК могут быть сведены к следующим принципам, учитывающим особенности подключения ...

0 комментариев