Навигация
Доверительные интервалы
2.5 Доверительные интервалы
Для того чтобы оценить достоверность оценок, вводят понятие доверительный интервал и доверительная вероятность.
|
![]()
где ![]() – математическое ожидание генеральной совокупности;
– математическое ожидание генеральной совокупности;
![]() - доверительная вероятность;
- доверительная вероятность;
![]() - оценка математического ожидания;
- оценка математического ожидания;
|
![]()
где ![]() - квантиль нормального распределения, получается обратным интерполированием из таблицы для функции распределения стандартного нормального закона. Вычисляется по формуле (2.9).
- квантиль нормального распределения, получается обратным интерполированием из таблицы для функции распределения стандартного нормального закона. Вычисляется по формуле (2.9).
|
|
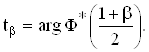
![]() - оценка дисперсии, вычисляется по формуле (2.10).
- оценка дисперсии, вычисляется по формуле (2.10).

Доверительный интервал для дисперсии определяется по формуле (2.11).
|
![]()
где ![]() – дисперсия генеральной совокупности;
– дисперсия генеральной совокупности;
![]() – оценка дисперсии.
– оценка дисперсии.
![]() – квантиль нормального распределения.
– квантиль нормального распределения.
Оценка стандартного отклонения в зависимости от закона распределения случайной величины имеет различное значение.
Для нормального закона распределения эта величина будет равна:
![]()
Для равномерного:

Ниже в таблицах 2.10-2.21 приведены доверительные интервалы математического ожидания исследуемых выборок.
-точный метод
Таблица 2.10 - Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 15,378 | 17,130 |
|
| 15,207 | 17,301 |
|
| 15,053 | 17,455 |
|
| 14,739 | 17,769 |
|
| 14,481 | 18,027 |
-грубый метод
Таблица 2.11 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 15,376 | 17,132 |
|
| 15,207 | 17,301 |
|
| 15,058 | 17,450 |
|
| 14,753 | 17,755 |
|
| 14,508 | 18,000 |
-точный метод
Таблица 2.12 - Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 15,811 | 16,566 |
|
| 15,738 | 16,639 |
|
| 15,673 | 16,704 |
|
| 15,542 | 16,835 |
|
| 15,408 | 16,940 |
-грубый метод
Таблица 2.13 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 15,795 | 16,553 |
|
| 15,722 | 16,626 |
|
| 15,657 | 16,691 |
|
| 15,526 | 16,822 |
|
| 15,420 | 16,928 |
-точный метод
Таблица 2.14 - Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 15,677 | 16,224 |
|
| 15,624 | 16,276 |
|
| 15,577 | 16,323 |
|
| 15,483 | 16,418 |
|
| 15,447 | 16,565 |
-грубый метод
Таблица 2.15 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 15,729 | 16,283 |
|
| 15,676 | 16,336 |
|
| 15,629 | 16,383 |
|
| 15,533 | 16,479 |
|
| 15,456 | 16,556 |
-точный метод
Таблица 2.16 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 15,742 | 17,595 |
|
| 15,561 | 17,775 |
|
| 15,399 | 17,938 |
|
| 15,066 | 18,270 |
|
| 15,084 | 18,788 |
-грубый метод
Таблица 2.17 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 16,018 | 17,854 |
|
| 15,843 | 18,029 |
|
| 15,687 | 18,185 |
|
| 15,369 | 18,503 |
|
| 15,112 | 18,760 |
-точный метод
Таблица 2.18 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 15,583 | 16,396 |
|
| 15,505 | 16,474 |
|
| 15,435 | 16,544 |
|
| 15,294 | 16,685 |
|
| 15,177 | 16,837 |
-грубый метод
Таблица 2.19 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 15,596 | 16,418 |
|
| 15,517 | 16,497 |
|
| 15,447 | 16,567 |
|
| 15,305 | 16,709 |
|
| 15,190 | 16,824 |
-точный метод
Таблица 2.20 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 15,521 | 16,063 |
|
| 15,469 | 16,115 |
|
| 15,423 | 16,161 |
|
| 15,329 | 16,255 |
|
| 15,178 | 16,302 |
-грубый метод
Таблица 2.21 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 15,462 | 16,018 |
|
| 15,408 | 16,072 |
|
| 15,361 | 16,119 |
|
| 15,264 | 16,216 |
|
| 15,187 | 16,293 |
Длины доверительных интервалов для математического ожидания при различных уровнях доверительной вероятности приведены в таблице 2.22.
Таблица 2.22 – Длины доверительных интервалов
| Длина интервала | |||||
|
|
|
|
|
| |
|
| 1,752 | 2,094 | 2,402 | 3,03 | 3,546 |
|
| 0,755 | 0,901 | 1,031 | 1,293 | 1,532 |
|
| 0,547 | 0,652 | 0,746 | 0,935 | 1,118 |
|
| 1,853 | 2,214 | 2,539 | 3,204 | 3,704 |
|
| 0,813 | 0,969 | 1,109 | 1,391 | 1,66 |
|
| 0,542 | 0,646 | 0,738 | 0,926 | 1,124 |
В таблицах 2.23 – 2.34 указаны доверительные интервалы дисперсии исследуемых выборок.
-точный метод
Таблица 2.23 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 25,059 | 32,793 |
|
| 24,452 | 33,693 |
|
| 23,926 | 34,524 |
|
| 22,914 | 36,280 |
|
| 22,095 | 37,873 |
-грубый метод
Таблица 2.24 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 26,084 | 30,950 |
|
| 25,619 | 31,415 |
|
| 25,205 | 31,829 |
|
| 24,362 | 32,672 |
|
| 23,681 | 33,353 |
-точный метод
Таблица 2.25 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 23,373 | 30,586 |
|
| 22,807 | 31,426 |
|
| 22,316 | 32,201 |
|
| 21,372 | 33,838 |
|
| 20,608 | 35,324 |
-грубый метод
Таблица 2.26 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 24,329 | 28,867 |
|
| 23,895 | 29,301 |
|
| 23,508 | 29,688 |
|
| 22,722 | 30,474 |
|
| 22,088 | 31,108 |
-точный метод
Таблица 2.27 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 22,258 | 29,128 |
|
| 21,719 | 29,928 |
|
| 21,252 | 30,666 |
|
| 20,354 | 32,225 |
|
| 19,626 | 33,640 |
-грубый метод
Таблица 2.28 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 23,169 | 27,491 |
|
| 22,756 | 27,904 |
|
| 22,388 | 28,272 |
|
| 21,639 | 29,021 |
|
| 21,035 | 29,625 |
-точный метод
Таблица 2.29 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 27,340 | 35,779 |
|
| 26,678 | 36,761 |
|
| 26,104 | 37,667 |
|
| 25,000 | 39,582 |
|
| 24,106 | 41,321 |
-грубый метод
Таблица 2.30 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 28,459 | 33,767 |
|
| 27,951 | 34,275 |
|
| 27,499 | 34,727 |
|
| 26,579 | 35,647 |
|
| 25,837 | 36,389 |
-точный метод
Таблица 2.31 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 26,575 | 34,777 |
|
| 25,931 | 35,732 |
|
| 25,374 | 36,613 |
|
| 24,301 | 38,474 |
|
| 23,431 | 40,164 |
-грубый метод
Таблица 2.32 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 27,662 | 32,822 |
|
| 27,168 | 33,316 |
|
| 26,729 | 33,755 |
|
| 25,835 | 34,649 |
|
| 25,114 | 35,370 |
-точный метод
Таблица 2.33 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 25,163 | 32,930 |
|
| 24,554 | 33,834 |
|
| 24,026 | 34,668 |
|
| 23,010 | 36,431 |
|
| 22,187 | 38,031 |
-грубый метод
Таблица 2.34 – Доверительные интервалы для СВ ![]() ,
, ![]()
|
| 26,193 | 31,079 |
|
| 25,726 | 31,546 |
|
| 25,310 | 31,962 |
|
| 24,463 | 32,809 |
|
| 23,780 | 33,492 |
В таблице 2.35 показано изменение длины доверительного интервала для дисперсии в зависимости от объема выборки и величины доверительной вероятности.
Таблица 2.35 – Длины доверительных интервалов
| Величина интервала | |||||
|
|
|
|
|
| |
|
| 7,734 | 9,241 | 10,598 | 13,366 | 15,778 |
|
| 7,213 | 8,619 | 9,885 | 12,466 | 14,716 |
|
| 4,322 | 5,148 | 5,884 | 7,382 | 8,590 |
|
| 8,439 | 10,083 | 11,563 | 14,582 | 17,215 |
|
| 8,202 | 9,801 | 11,239 | 14,173 | 16,733 |
|
| 7,767 | 9,280 | 10,642 | 13,421 | 15,844 |
Анализируя полученные данные можно заметить, что при увеличении уровня доверительной вероятности увеличивается величина доверительного интервала, а при увеличении объема выборки она уменьшается. Это справедливо как для доверительных интервалов математического ожидания, так и для дисперсии. [3]
Похожие работы
... отпуска может быть на 10–20оС ниже, а его продолжительность на 20–25% меньше, чем первого отпуска. Охлаждение после отпуска проводится на воздухе. 1.1.5 Влияние термической обработки на свойства штамповых сталей Служебные свойства штампового инструмента и его стойкость в значительной степени определяются соответствующим назначением марки стали, ее термообработкой и условиями эксплуатации ...
... о начавшихся в них процессах деградации, которые в дальнейшем приведут к условным отказам. В этом случае выбросы являются закономерными, обусловлены физическими процессами и их нельзя исключать из дальнейшего рассмотрения при статистической обработке результатов испытаний. Поэтому для принятия того или иного решения проводят тщательный комплексный анализ возможных причин указанных отклонений. ...
... в процессе обучения, необходима разработка совершенно новых подходов к работе с таким видом информационных ресурсов как базы данных. Глава 2.Технология использования баз данных математических задач в процессе подготовки учащихся к ЕГЭ по математике 2.1 Реализация модели В соответствии с теорией поэтапного формирования умственных действий учащихся, подготовку к сдаче единого ...
... плана ФЭ. Большое разнообразие моделей РК приводит к необходимости использования разнообразных способов и технических средств для измерения их параметров. Как правило, статические и динамические параметры РК измеряют на разных технологических установках. Методы построения средств измерения для идентификации моделей РК могут быть сведены к следующим принципам, учитывающим особенности подключения ...

0 комментариев