Необхідні поняття, факти і нотація із інших математичних дисциплін
Відношення і предикати
Коли <q; a1., am> – кінцевий стан, то
Аналгічно до класів KS-1 схем алгоритмів і ¶нтерпретацій KI-1 введемо, відпвидно, класи KS-2 і KI-2
Операторні та предикатні алгоритми -ІІ
Наслідок. Існує обчислювана функція h, для якої обидві проблеми «x Î Dom(h)» і «х Î Ran(h)» нерозв'язні
Теорема. Нехай c – довільне число. Наступні проблеми нерозв'язні
Логіка висловлень (пропозиційна логіка) [1] – одна з базових теорій математичної логіки, на якій базуються більш складні формальні логіки
Необхідно побудувати кон’юктивну нормальну форму для формули А логіки висловлень, де
Навигация
Необхідні поняття, факти і нотація із інших математичних дисциплін
Алгоритмічні проблеми
54576
знаков
5
таблиц
0
изображений
2. Необхідні поняття, факти і нотація із інших математичних дисциплін
Тут дано огляд математичних понять і роз'яснимо позначення і терміни, що будуть використані надалі.
1. Множини
Для позначення множин звичайно будуть використовуватися прописні букви А, В, С…. Тут х
А позначає, що х є елементом множини А чи належить множині А, а х
А означає, що х не належить множині А. Позначення {х/… х…}, де…х… є деяке твердження, що включає х, означає множину всіх об'єктів х, для яких…х… вірно. Так, {х/х є парним натуральним числом} є множина {0,2, 4,6,…}.
Якщо А, В суть множини, то запис A 
В означає, що А міститься (як частина) в В (чи А є підмножиною В); запис А
В означає, що АВ, але А
В (тобто А є власною підмножиною В). Об'єднання множин А, В, є множина {х| хА чи хВ (чи відразу двом множинам А, В)} і позначається А U В; перетин А, В є множина {х/хА і хВ} і позначається через А
В. Різниця (чи відносне доповнення) множин А, В є множина {х / хА і хВ} і позначається А\В.
Порожня множина позначається через 0. Стандартний символ N позначає множину натуральних чисел {0, 1, 2, 3,…}. Якщо А – множина натуральних чисел (тобто АN), то А позначає доповнення до А до N, тобто N\А. Через N+ позначається множина додатніх натуральних чисел {1,2,3,…}, а множина цілих чисел позначається через Z.
Упорядкована пара елементів х, у позначається (х, у); таким чином, (х, у)(у, х). Картезіанським, чи декартовым, добутком множин А и В називається множина {(х, у)/хА, уВ}, і позначається вона через А
В.
Більш узагальнено, запис (х1…, хn) позначає упорядкований n-набір (п-ку) елементів х1,…, хn; часто цей n-набір позначається однією жирною буквою х. Якщо А1,…, Аn суть множини, те А1…Аn позначає множину n-ок {(х1,…, хn)/х1 А1 і х2 А2…хnАn}. Добуток АА…А (п разів) скорочено позначають як Аn; а А1 означає просто А.
2. Функції
Ми припускаємо, що читач знайом з основним поняттям функції і розходженням між функцією f і окремим значенням f(х) на даному х, на якому функція визначена. Областю (визначення) функції f називається множина {x/f(x) визначена} і позначається Dom(f); ми будемо говорити, що f (х) не визначена, якщо xDom(f). Множина {f (х) | х Dom (f)} називається множиною значень, чи образом (range), функції f і позначається через Ran (f). Якщо А и В – множиниі, то будемо говорити, що f є функція з A в В, якщо Dom (f)A и Ran(f)В. Коли Dom(f)=A, буде застосовуватися позначення f: A
r.
Функція називається ін’єктивною, якщо з х, у Dom (f) і ху випливає f(х) f (у). Для ін’єктивної функції f через f -1 позначається функція, зворотня до f, тобто така єдина функція g, що Dom (g)=Ran (f) g (f(x))=x для всіх хDom (f). Функція f з А в В називається сюр’єктивною, якщо Ran(f)=B.
Якщо f: A В и функція f ин’єктивна (сюр’єктивна), то f називається ін'єкцією (з А в В) (сюр’єкцією (з А в В)). Функція, що є одночасно ін'єкцією і сюръекцией, називається биекцией.
Припустимо, що f є функцією, а Х – множина. Обмеженням f на Х називається функція з областю визначення ХDom(f), значення якої в кожному х Х Dom (f) дорівнює f(x).
Обмеження f на Х позначається через f|X. Ran (f|X) позначається через f(X). Якщо Y – множина, то прообразом Y відносно f називається множина f-1(Y)={x|f(x)Y}. (Помітимо, що прообраз визначений навіть тоді, коли функція не ин’єктивна.)
Якщо f, g-функції, то будемо говорити, що g продовжує f, коли Dom (f) Dom (g) і f(х) = g (х) для всіх х Dom (f); у коротшому запису: f=g/Dom(f). Це відношення функцій f, g записується як f g.
Композиція двох функцій f і g є функція з областю визначення {x/xDom(g) і g(x)Dom(f)}, значення якої, коли вона визначена, є f (g(x)). Цю функцію позначають через f
g.
Через f0 позначаємо ніде не визначену функцію; тобто Dom(f0)=Ran(f0)=0. Очевидно, що f0=g|0 для будь-якої функції g.
В обчисленнях нам часто будуть зустрічатися функції чи вирази, що включають функції, що не усюди визначені. У таких випадках дуже зручне наступне позначення. Нехай a(x) і b(х) – вирази, що включають змінні х=(х1,…, хn). Тоді запис а(x) 
b(x) означає, що для кожного х вираження а(x) і b(x) або одночасно визначені і рівні, або обидва не визначені. Так, наприклад, для функцій f і g запис f(x)g(x) означає, що f=g; і для довільного числа y запис f(x) y означає, що f(x) визначена і дорівнює y (оскільки y завжди визначене).
Функції від натуральних чисел. У більшій частині цієї книги ми будемо мати справу з функціями від натуральних чисел, тобто з функціями з Nn в N для різних п, здебільшого для п = 1 чи 2.
Функція f з Nn в N називається п-місною функцією. Значення f на п-кі (x1,…, хn) Dom (f) записується як f(x1,…, xn) чи f(x), якщо x представляє (x1,…, xn). У багатьох книгах і статтях термін часткова функція використовується для позначення функції з Nn у N, область визначення якої не обов'язково збігається з Nn. Для нас слово функція означає часткову функцію. Проте при нагоді ми будемо писати «часткова функция», щоб підкреслити її можливу «не усюди визначеність». Тотальною функцією з Nn у N ми називаємо функцію з Nn у N), область визначення якої є всі Nn. l
Ми затушовуємо розходження між функціями і їхнім значеннями в різних крапках, особливо у випадку теоретико-числових функцій у двох досить стандартних і недвозначних ситуаціях. По-перше, ми допускаємо такі фрази як «Нехай f(x1,…, xn) – функція…», що означає, що f є n-місною функцією. По-друге, ми часто описуємо функцію в термінах її значення, що задається деякою формулою. Наприклад, «функція х2» означає «одномісна функція f, значення якої в кожному х N є х2»; аналогічно «функція х + у» означає «двомісна функція», значення якої в кожній парі (х, у) N2 є х+ у.
Функцію, тотожно рівну 0 на N, ми позначаємо через 0, і взагалі для т N функцію NN, значення якої усюди дорівнює т, ми позначаємо жирним символом т.
Похожие работы
... число эпох функционирования алгоритма, или определение его сходимости, обычно путем сравнивания приспособленности популяции на нескольких эпохах и остановки при стабилизации этого параметра. 3. Непрерывные генетические алгоритмы. Фиксированная длина хромосомы и кодирование строк двоичным алфавитом преобладали в теории генетических алгоритмов с момента начала ее развития, когда были получены ...
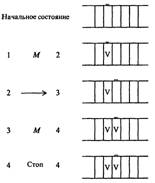
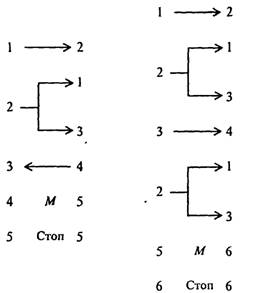
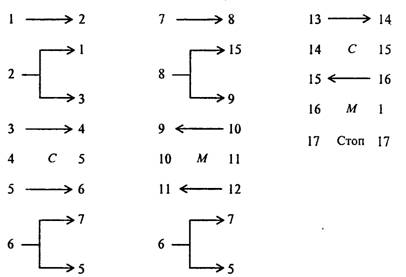
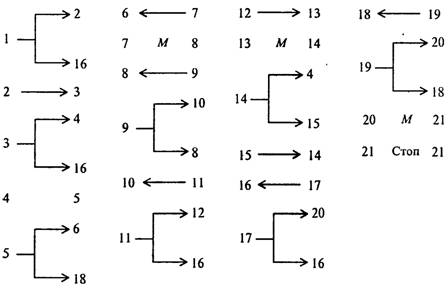
... в состояние qj, заменяя содержимое ячеек соответственно символами аb1 - аbк, то после этого ленты соответственно сдвигаются в направлениях k1... kk. До сих пор принималось, что различные алгоритмы осуществляются на различных машинах Тьюринга, отличающихся набором команд, внутренним и внешним алфавитами. Однако, можно построить универсальную машину Тьюринга, способную выполнять любой алгоритм ...
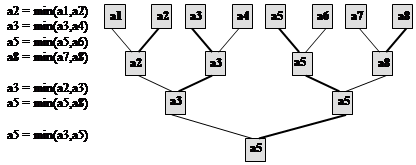
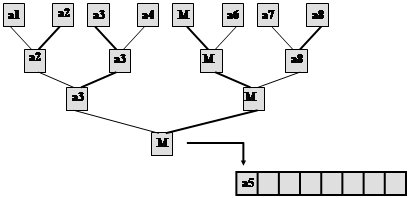
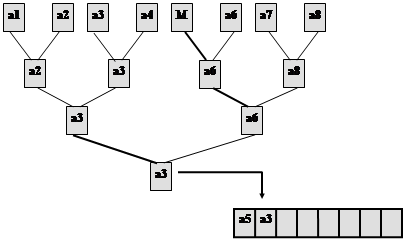
... M2(n) = O(l n), C2(n) = O(l n). Оскільки l = log2n, M2(n)=O(n log2 n)), C2(n)=O(n log2 n), Але З(n) = C1(n) + C2(n), M(n) = M1(n) + M2(n). Тому що C1(n) < C2(n), M1(n) < M2(n), остаточно одержуємо оцінки складності алгоритму TreeSort за часом: M(n) = O(n log2 n), C(n) = O(n log2 n), У загальному випадку, коли n не є ступенем 2, сортуюче дерево будується трохи інакше. “Зайвий” елемент ...
... U4 сравнения двух целых чисел оставляем читателю в качестве упражнения. Замечание: исходное слово надо задать в форме * Для нормальных алгоритмов Маркова справедлив тезис, аналогичный тезису Тьюринга. Тезис Маркова: Для любой интуитивно вычислимой функции существует алгоритм, ее вычисляющий. Построение алгоритмов из алгоритмов. До сих пор, строя ту или иную МТ, или НАМ мы каждый раз ...
0 комментариев