Навигация
Аналгічно до класів KS-1 схем алгоритмів і ¶нтерпретацій KI-1 введемо, відпвидно, класи KS-2 і KI-2
3. Аналгічно до класів KS-1 схем алгоритмів і ¶нтерпретацій KI-1 введемо, відпвидно, класи KS-2 і KI-2.
Нехай E = a1., an – деякий алфавит. Через E* позначимо множину всіх слів в алфавібі E, включаючи однолітерні слова виду 'ai' і пусте слово e =''.
Введемо на E* деякі стандартні функції і предикати. Якщо w = x1x2..xm і v = y1y2..yk – слова iз E*, то
а) con (w, v) = wv = x1x2..xmy1y2..yk, con (e, v) =con (v, e) = v;
б) del(w) = d(w) = x2x3..xm, del(e) = e;
в) для всіх літер ai із E предикат hai(w) = T (істино), коли x1 = ai, і hai(w) = F (хибно), коли перша літера x1 у слові w не дорівнює ai (1 <= i <= m), причому для всіх i
hai(e) = F.
Якщо а – довільна літера із E*, то через (a^n) позначається слово, що склдається із n літер a.
Клас схем програм KS-2 містить (n + 1) унарних функціональних символів fa1, fa2., fan, g, один константний символ b і n унарних предикатних символів pa1, pa2., pan,
В класі інтерпретацій KI-2 схем із KS-1 множина D завжди співпадає з множиною E* всіх слів в алфавіті E, а кожне відображення I із KI-2 задовільняє наступним вимогам:
1) I(b) = е;
2) I (fai(x)) = con (I(x), 'ai')= I(x) ai для всіх літер ai із E;
3) I (g(x)) = del (I(x));
4) I (pai(x)) = hai (I(x)) для всіх літер ai із E;
5) I(xi) єE* для всіх вхідних змінних СОА і СПА виду (6), (7), і I(y) = e для всіх інших змінних із пам'яті вищезгаданих схем алгоритмів.
Замінивши у (5) сімволи fai, g, b і hai згідно з інтерпретацією I із класу KI-2 ми отримаємо програмноподібну структуру, рядки якої будемо називаті командами. Тому схеми алгоритмів (6) і (7) iз класу KS-2 далі інтерпретуються, як відповідні алгоритми (програми) iз класу прграм KП-2, функціонування яких подібно до функціонування програм, що написані на мовах програмування типу Паскаль, коли ці програми працюють на даних типу string. Ясно, що функціонуваня команд програм із класу КП-2 аналгічно, з точністю до інтерпретації символів її схеми, до функціонуваня команд програм із класу КП-1, яке було описано вище.
Зауважимо також, що по аналогії з N-БРМ БN можна ввести E-БРМ БE, що реалізує програму із КП-2, а також NE-БРМ БNE. БNE можна розглядати як «об'єднання» програм ПN i ПE для БN i БE в тому сенсі, що множини регістрів БN i БE не перетинаються, але вони мають загальний блок управління (i спільні мітки), в якій поміщена спільна програма ПNE, в яку входять всі команди, як із ПN так і із ПE.
Часткові або всюдиозначенні функцію g: E*вх –>E*вх, яка задана на множині слів довільного алфавіту E, або предикат P: E* –> T, F, будемо називати E – рекурсивною функцією (предикатом), або RE-функцією (RE-предикатом), якщо існує програма із класу КП-2 П1g, що обчислює g (P).
Як відомо [1], [2], за допомгою кодуючої функції доводиться, що, в певному сенсі, клас R-функцій (R-предикатів) і клас RE-функцій (RE-предикатів) є еквівалентні.
Приклади доведення по побудові RE-рекурсивності функцій і предікатьв наведені далі.
Побудуємо алгоритм, що обчислює функцію
z:= f1 (x, y) = x + y.
x, y! z
| q10 q11 q12 q13 q14 q15 q16 q17 q18 q19 | x1 = x (q11, q11) y1 = y (q12, q12) z1 = 0 (q13, q13) P0 (x1) (q16, q14) z1 = z1 + 1 (q15, q15) x1 = x1 -^ 1 (q13, q13) P0 (y1) (q19, q17) z1 = z1 + 1 (q18, q18) y1 = y1 -^ 1 (q16, q16) z = z1 (Я, Я) |
Побудуємо алгоритм (не оптимальний), що заносить в z значення функції добутку x i y, тобто z:= f1 (x, y) = x * y.
x, y! Z
| q20 q21 q22 q23 | x2 = x (q21, q21) y2 = y (q22, q22) z2 = 0 (q23, q23) P0 (y2) (q25, q10) |
| q10 q11 q12 q13 q14 q15 q16 q17 q18 q19 | x1 = z2 (q11, q11) y1 = x (q12, q12) z1 = 0 (q13, q13) P0 (x1) (q16, q14) z1 = z1 + 1 (q15, q15) x1 = x1 -^ 1 (q13, q13) P0 (y1) (q19, q17) z1 = z1 + 1 (q18, q18) y1 = y1 -^ 1 (q16, q16) z2 = z1 (q24, q24) |
| q24 q25 | z2 = z1 (q23, q23) z = z2 (Я, Я) |
Нехай алфавіт Е = a, b. Побудуємо алгоритм, що обчислює предикат Pe(w), де Pe(w) = T тоді і тільки тоді, коли w є пусте слово із E*, тобто w = e.
x! q [.t.], q [.f.]
q10 x1 = x (q11, q11)
q11 ha(x1) (q [.f.], q12)
q12 hb(x1) (q [.f.], q [.t.])
Побудуємо алгоритм (не оптимальний), що заносить в z значення функції con (x, y) = xy, тобто z:= g1 (x, y) = con (x, y) = = xy для слів із Е = a, b.
x, y! Z
| q20 q21 q22 | x2 = x (q21, q21) y2 = y (q22, q22) z2 = e (q10, q10) |
| q10 q11 q12 | x1 = y2 (q11, q11) ha(x1) (q22, q12) hb(x1) (q22, q28) |
| q22 q23 q24 | ha(y2) (q23, q25) x2 = con (x2, a) (q24, q24) y2 = del(y2) (q22, q22) |
| q25 q26 q27 q28 | hb(y2) (q26, q10) x2 = con (x2, b) (q27, q27) y2 = del(y2) (q25, q25) z = x2 (Я, Я) |
Похожие работы
... число эпох функционирования алгоритма, или определение его сходимости, обычно путем сравнивания приспособленности популяции на нескольких эпохах и остановки при стабилизации этого параметра. 3. Непрерывные генетические алгоритмы. Фиксированная длина хромосомы и кодирование строк двоичным алфавитом преобладали в теории генетических алгоритмов с момента начала ее развития, когда были получены ...
... в состояние qj, заменяя содержимое ячеек соответственно символами аb1 - аbк, то после этого ленты соответственно сдвигаются в направлениях k1... kk. До сих пор принималось, что различные алгоритмы осуществляются на различных машинах Тьюринга, отличающихся набором команд, внутренним и внешним алфавитами. Однако, можно построить универсальную машину Тьюринга, способную выполнять любой алгоритм ...
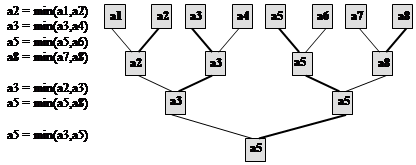
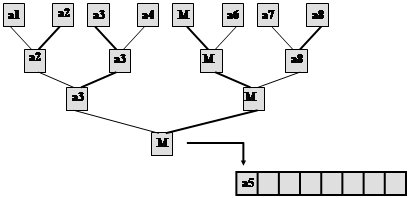
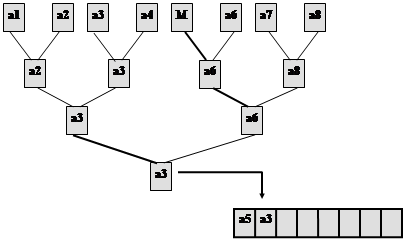
... M2(n) = O(l n), C2(n) = O(l n). Оскільки l = log2n, M2(n)=O(n log2 n)), C2(n)=O(n log2 n), Але З(n) = C1(n) + C2(n), M(n) = M1(n) + M2(n). Тому що C1(n) < C2(n), M1(n) < M2(n), остаточно одержуємо оцінки складності алгоритму TreeSort за часом: M(n) = O(n log2 n), C(n) = O(n log2 n), У загальному випадку, коли n не є ступенем 2, сортуюче дерево будується трохи інакше. “Зайвий” елемент ...
... U4 сравнения двух целых чисел оставляем читателю в качестве упражнения. Замечание: исходное слово надо задать в форме * Для нормальных алгоритмов Маркова справедлив тезис, аналогичный тезису Тьюринга. Тезис Маркова: Для любой интуитивно вычислимой функции существует алгоритм, ее вычисляющий. Построение алгоритмов из алгоритмов. До сих пор, строя ту или иную МТ, или НАМ мы каждый раз ...

0 комментариев