Необхідно побудувати кон’юктивну нормальну форму для формули А логіки висловлень, де

1. Необхідно побудувати кон’юктивну нормальну форму для формули А логіки висловлень, де

A = (p -> (q -> r)) -> ((p /\ s) -> r).

Використаємо алгоритм із розділу 1.2. Кожна з нижченаведених формул еквівалентна А.

Етап 1 (виключення імплікацій).

(p -> (q -> r)) -> ((p /\ s) -> r),

^ (p -> (q -> r)) \/ ((p /\ s) -> r),

^ (^p \/ (q -> r)) \/ (^(p /\ s) \/ r),

^ (^p \/ (^q \/r)) \/ (^(p /\ s) \/ r),

Етап 2.

(^ ^p /\ ^ (^q \/r)) \/ ((^p \/ ^s) \/ r),

(^ ^p /\ (^ ^q /\ ^r)) \/ ((^p \/ ^s) \/ r),

(p /\ (q /\ ^r)) \/ ((^p \/ ^s) \/ r).

Етап 3.

a) (p \/ ((^p \/ ^s) \/ r)) /\ ((q /\ ^r) \/ \/ ((^p \/ ^s)

\/ r))

b) (p \/ (^p \/ ^s) \/ r)) /\ /\ (q \/ (^p \/ ^s) \/ r) /\

(^r \/ (^p \/ ^s) \/r);

c) (p \/ ^p \/ ^s \/ r) /\ /\ (q \/ ^p \/ ^s \/ r) /\ (^r

\/ ^p \/ ^s \/ r);

d) T /\ (q \/ ^p \/ ^s \/ r) /\ T;

e) (q \/ ^p \/ ^s \/ r).

Ми отримали, що КНФ В = (q \/ ^p \/ ^s \/ r) формули А складається з одного диз’юнкта.

Приклад

2. Необхідно перевірити за допомогою метода резолюцій, чи є КНФ S суперечністю, де

S = {p \/q, p /\ r, ^q \/ ^r, ^p}.

Диз’юнкти зручно перенумерувати. Отримаємо список:

1. p \/q

2. p \/ r

3. ^q \/ ^r

4. ^p

Далі обчислюються резольвенти і додаються до S. У нижченаведеному списку кожний диз’юнкт – резольвента деяких попередніх диз’юнктів. Номера їх наводяться з права від відповідної резольвенти

5. p \/ ^r 1,3

6. q 1,4

7. p \/ ^q 2,3

8. r 2,4

9. p 2,5

10. ^r 3,6

11. ^q 3,8

12. ^r 4,5

13. ^q 4,7

14. Л 4,9

Отримали, що із КНФ S виводиться пустий диз’юнкт Л, тобто S є суперечністю (не виконуваною формулою).

(Теорема про нерозв'язність числення предикатів)

Найпростішою логічною системою, у якій знаходять висвітлення деякі аспекти математичного мислення, є числення висловлень. У цьому численні складні твердження будуються з деяких основних висловлень за допомогою символів, що позначають логічні зв'язки «не», «і», «чи» і «волоче». Досить легко переконатися в тому, що якщо числення висловлень визначене досить акуратно, то воно розв'язне. Це означає, що існує ефективна процедура рішення питання про те, чи є те чи інше твердження цього числення (тотожно) істинним, тобто справедливим у всіх можливих ситуаціях. Алгоритм цього дається методом істиннісних таблиць, добре знайомим багатьом читачам.

Більш широкими можливостями, ніж числення висловлень, володіє логічна система, що називається численням предикатів (першого порядку). мовою цього числення можна формалізувати значну частину всієї математики. Основні твердження в ньому формуються із символів, що представляють індивідуальні об'єкти (чи елементи), і предикатів і функцій на них. Складні твердження будуються з основних з використанням логічних символів числення висловлень, а також символів " і $.

Мається точне поняття доведення твердження числення предикатів, причому твердження доводиться тоді і тільки тоді, коли воно істинно. У 1936 році Черч показав, що доведеність (і, отже, істинність) у численні предикатів нерозв'язна на відміну від більш простого пропозиціонального числення. (Гільберт вважав цей результат самим фундаментальної результатом, що стосується нерозв'язності, у всій математиці.)

Просте доведення нерозв'язності проблеми істинності можна дати з використанням МНР, хоча це вимагає деякого знайомства з численням предикатів. Читачу, що не знайомий з початками логіки предикатів, ми радимо пропустити приведений нижче зразок доведення.

5.1. Теорема. Проблема істинності числення предикатів першого порядку нерозв'язна.

Доведення. (Тим, хто не знайомий з численням предикатів, рекомендується пропустити.)

Нехай Р – деяка програма в стандартному виді, що містить команди I₁,…, I_s, і нехай u=r(P) (визначення див. § 2 р. 2). Ми будемо використовувати наступні позначення символів числення предикатів:

O – індивідний символ,

' – символ одномісної функції (значення якої на х дорівнює х'),

R-символ (u+1) – місного відношення,

x₁, x₂,…, x_a, у – символи індивідних змінних.

Далі, для будь-якої команди I_i, можна записати твердження числення предикатів t_i, що описує результат виконання команди I_i. При цьому ми використовуємо символ Ù для позначення зв'язки «і» і символ ® для позначення імплікації. Твердження t_i, визначається в такий спосіб:

(a)        якщо I_i=Z(n), тo t_i, є твердження

"x₁ … "x_u: R (x₁, …, x_n, …, x_u, i)®R (x₁, …, O, …, x_u, i ¢)

(b)        якщо I_i=S(n), то t_i, є твердження

"x₁ … "x_u: R (x₁, …, x_n, …, x_u, i)®R (x₁, …, x_n¢, …, x_u, i ¢)

(c) якщо I_i=T (m, n), тo t_i, є твердження

"x₁ … "x_u: R (x₁, …, x_n, …, x_u, i)®R (x₁, …, x_m, …, x_u, i¢)

(d) якщо I_i=J (m, n, q), тo t_i, є твердження

"x₁ … "x_u: R (x₁, …, x_u, i)®((x_m = x_n ®R(x₁, …, x_u, q))Ù(x_m ¹ x_n ®R(x₁, …, x_u, i¢)))

Нехай тепер для будь-якого а Î N символ s_a позначає твердження.

(t₀Ùt₁Ù…Ùt_sÙ R (a, O,… O, 1))®$x₁ … $x_u R(x_{1, …,} x_u, s+1)

де t₀ є твердження "x"y((х'=у® x=y) Ù x¢¹O). (Це гарантує нам, що при будь-якій інтерпретації з т, n

Î N і m=n випливає, що т=п.)

Твердження R (a, O,…, О, 1) відповідає вихідному стану

а будь-яке твердження R(x₁,…, х_u, s +1) відповідає зупинці (оскільки немає команди I_s+1). Ми покажемо, що

(*) Р (а)¯Ûs_a істинно.

Припустимо спочатку, що Р(а)¯ і що мається структура, у якій твердження t_0,…, t_s, і R (a, O,…, O, 1) виконуються. За допомогою тверджень t_0,…, t_s, ми одержуємо, що кожне з тверджень R(r₁,…. r_u, k),

що відповідають послідовним станам обчислення, також виконується. Зрештою ми приходимо до того, що для деяких b₁,…, b_u Î N виконується твердження про зупинку R(b₁,…, b_u, s+1) і, отже, виконується твердження $x₁ …$x_u R(x₁,…, x_u, s+1). Таким чином, твердження s_a істинно.

Знову, якщо твердження s_a істинно, то воно виконується, зокрема, у структурі N, причому предикатний символ R інтерпретується як предикат R_a, для якого

R_a(a_1,…, а_u, k)ºНа деякому етапі обчислення Р (а) у регістрах містяться числа а₁, a₂,…, a_u, 0, 0,…, а наступна команда є I_k.

Тоді твердження t_0,…, t_s, і R (a, O,…, O, 1) також виконуються в цій структурі, а отже, і твердження $x₁ …$x_u R(x₁,…, x_u, s+1). Звідси Р(а)¯.

Якщо в якості Р узяти програму, що обчислює функцію y_u (x, х), то співвідношення еквівалентності (*) зводить проблему «x Î W_x» до проблеми «s істинно». Звідси випливає, що остання проблема нерозв'язна. ÿ

Математична логіка буяє результатами, що стосуються можливості розв'язання і нерозв'язності. Звичайно мова йде про задачі, у яких необхідно установити, чи буде деяке твердження істинним у всіх математичних структурах визначеного типу. Наприклад, було показано, що проблема «s є твердження, істинне для всіх груп» є нерозв'язною (s тут є твердження мовою числення предикатів першого порядку, що відповідає теорії груп), тоді як проблема «s є твердження, істинне для всіх абелевих груп» розв'язна. (При цьому прийнято говорити, що теорія груп першого порядку нерозв'язна, у той час як теорія абелевых груп першого порядку розв'язна.) Як було показано Тарським [1951], проблема «твердження s істинне в полі дійсних чисел» є розв'язної. З іншого боку, як ми побачимо в р. 8, багато проблем, зв'язаних з формалізацією арифметики натуральних чисел, нерозв'язні.

З іншими прикладами, а також з доведеннями багатьох результатів, що стосуються можливості розв'язання і нерозв'язності в математичній логіці, читач може ознайомитися в книгах Тарського, Мостовського і Робінсона [1953] чи Булоса і Джефрі [1974], а також Єршова [1981]*.

Похожие работы

Непрерывные генетические алгоритмы

Скачать

33080

5

4

... число эпох функционирования алгоритма, или определение его сходимости, обычно путем сравнивания приспособленности популяции на нескольких эпохах и остановки при стабилизации этого параметра. 3. Непрерывные генетические алгоритмы. Фиксированная длина хромосомы и кодирование строк двоичным алфавитом преобладали в теории генетических алгоритмов с момента начала ее развития, когда были получены ...

Формализация понятия "алгоритм"

Скачать

18213

1

5

... в состояние qj, заменяя содержимое ячеек соответственно символами аb1 - аbк, то после этого ленты соответственно сдвигаются в направлениях k1... kk. До сих пор принималось, что различные алгоритмы осуществляются на различных машинах Тьюринга, отличающихся набором команд, внутренним и внешним алфавитами. Однако, можно построить универсальную машину Тьюринга, способную выполнять любой алгоритм ...

Быстрые алгоритмы сортировки

Скачать

26020

3

4

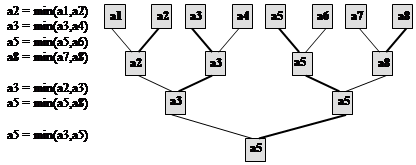
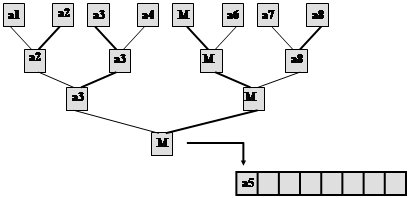
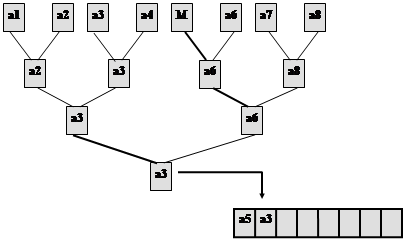
... M2(n) = O(l n), C2(n) = O(l n). Оскільки l = log2n, M2(n)=O(n log2 n)), C2(n)=O(n log2 n), Але З(n) = C1(n) + C2(n), M(n) = M1(n) + M2(n). Тому що C1(n) < C2(n), M1(n) < M2(n), остаточно одержуємо оцінки складності алгоритму TreeSort за часом: M(n) = O(n log2 n), C(n) = O(n log2 n), У загальному випадку, коли n не є ступенем 2, сортуюче дерево будується трохи інакше. “Зайвий” елемент ...

Нормальные Алгоритмы Маркова. Построение алгоритмов из алгоритмов.

Скачать

10075

2

1

... U4 сравнения двух целых чисел оставляем читателю в качестве упражнения. Замечание: исходное слово надо задать в форме  * Для нормальных алгоритмов Маркова справедлив тезис, аналогичный тезису Тьюринга. Тезис Маркова: Для любой интуитивно вычислимой функции существует алгоритм, ее вычисляющий. Построение алгоритмов из алгоритмов. До сих пор, строя ту или иную МТ, или НАМ мы каждый раз ...