Необхідні поняття, факти і нотація із інших математичних дисциплін
Відношення і предикати
Коли <q; a1., am> – кінцевий стан, то
Аналгічно до класів KS-1 схем алгоритмів і ¶нтерпретацій KI-1 введемо, відпвидно, класи KS-2 і KI-2
Операторні та предикатні алгоритми -ІІ
Наслідок. Існує обчислювана функція h, для якої обидві проблеми «x Î Dom(h)» і «х Î Ran(h)» нерозв'язні
Теорема. Нехай c – довільне число. Наступні проблеми нерозв'язні
Логіка висловлень (пропозиційна логіка) [1] – одна з базових теорій математичної логіки, на якій базуються більш складні формальні логіки
Необхідно побудувати кон’юктивну нормальну форму для формули А логіки висловлень, де
Навигация
Теорема. Нехай c – довільне число. Наступні проблеми нерозв'язні
Алгоритмічні проблеми
54576
знаков
5
таблиц
0
изображений
1.6. Теорема. Нехай c – довільне число. Наступні проблеми нерозв'язні.
(а) (Проблема входу) «c Î Wx» (чив еквівалентному формулюванні «Рx (с)¯», чи «c Î Dom (фx)»);
(b) (Проблема виходу) «c Î Ex» (чи в еквівалентному формулюванні «с Î Ran (фx)»).
Доведення. Ми можемо звести проблему «х Î Wx» до обох цих проблем одночасно. Розглянемо функцію f (х, у), визначену в такий спосіб:
y, якщо х Î Wx
f (x, y)=
не визначена в протилежному випадку
(Маючи на увазі використовувати s-m-n-теорему, ми будемо розглядати функції gx, для яких gx(y)@ f (x, у). Функцію f ми вибрали таким чином, що c Î Dom (gx)Û х Î Wx Ûc Î Ran(gx).) У силу тези Черча функція f обчислювана, так що s-m-n-теорема дає тотальну обчислювану функцію k, таку, що f (х, у)@ фk(x)(y). З визначення f ми бачимо, що
x Î WxÞWk(x)=Ek(x)=N
так що c Î Wk(x) і c Î Ek(x),і
x Ï WxÞWk(x)=Ek(x)=Æ
так що c Ï Wk(x) і c Ï Ek(x). Тим самим ми звели проблему «x Î Wx» до кожної з проблем «c Î Wx » і «c Î Ex «.
Завершуючи Доведення пункту (а) більш докладно, ми бачимо, що якщо g-характеристична функція проблеми «c Î Wx », то
1, якщо x Î Wx,
g (k(x))=
0, якщо x Ï Wx
Ця функція не є обчислюваною (теорема 1.1), так що функція g теж не може бути обчислюваною. Отже, проблема «c Î Wx » нерозв'язна.
Докладне доведення пункту (Ь) проводиться аналогічно. ÿ
Ми закінчимо цей параграф одним дуже загальним результатом про нерозв'язність, з якого негайно випливають теореми 1.4 і 1.6. При цьому ми знову скористаємося для зведення проблеми «х Î Wx »
s-m-n-теоремою.
1.7. Теорема (теорема Райса). Нехай ВÍ b1 і B¹ Æ, b1. Тоді проблема «фx Î B» нерозв'язна.
Доведення. Співвідношення для розв'язних множин (теорема 2–4.7) показують, що проблема «фx Î B» розв'язна тоді і тільки тоді, коли розв'язна проблема «фx Î b1 \ B». Тому без втрати загальності ми можемо вважати, що ніде не визначена функція fÆ не належить B (якщо це не так, то твердження можна довести для b1 \ B).
Виберемо деяку функцію g Î B. Розглянемо функцію f (x, у), що задається так:
g(y), якщо x Î Wx,
f (x, y)@
не визначена, якщо x Ï Wx.
Користаючись s-m-n-теоремою, ми одержуємо тотальну обчислювану функцію k (x), таку, що f (x, у) @ фk(x) (y),). Таким чином, ми бачимо, що
x Î Wx Þ фk(x) =g, тобто фk(x) Î B
x Ï Wx Þ фk(x) =fÆ, тобто фk(x) Ï B
Це значить, що за допомогою обчислюваної функції k ми звели проблему «х Î Wx » до проблеми
«фх Î В». Тепер уже стандартним чином можна покласти, що проблема «фх Î В» нерозв'язна.
Теорема 1.4, наприклад, негайно випливає з теореми Райса, якщо взяти В ={0}, а теорема 1.6 (а) – якщо взяти В={g Î b1:c Î Dom(g)}. Аналогічно можна скористатися теоремою Райса і у наступних вправах.
1.8. Вправи.
1. Покажіть, що наступні проблеми нерозв'язні.
(a) «х Î Ех «. (Указівка. Скористайтеся діагональним методом чи зведіть до цієї проблеми проблему
«x Î Wx» за допомогою s – m- n – теореми.)
(b) «Wx=Wy «. (Указівка. Зведіть до цієї проблеми проблему «функція фx тотальна».)
(c) «фx(х)=0».
(d) «фx(y)=0».
(e) «х Î Еу «.
(f) «функція фx тотальна і постійна».
(g) «Wx=Æ».
(h) «множина Еx нескінченна».
(i) «фх=g», де g є будь-яка фіксована обчислювана функція.
2. Покажіть, що не існує тотальної обчислюваної функції f (x, у), що володіє наступними властивістями: якщо програма Рх(у) зупиняється, те це відбувається за f (x, у) чи менше кроків (Указівка. Покажіть, що якби така функція існувала, те проблема зупинки була б розв'язна.)
Можливість розв'язання і нерозв'язання в інших областях математики. У багатьох областях математики виникають проблеми загального характеру, для яких має сенс неформальне поняття можливості розв'язання. Звичайно такі проблеми стосуються кінцевих об'єктів деякої конкретної області. У цьому випадку поняттю можливості розв'язання тієї чи іншої властивості, що стосується цих об'єктів, можна надати точний зміст, використовуючи придатне кодування натуральними числами.
Виявленню розв'язних і нерозв'язних проблем у самих різних математичних ситуаціях присвячено багато досліджень.
6. Дані і знання. Логіка висловлень (ЛВ) в представленні знаньПохожие работы
... число эпох функционирования алгоритма, или определение его сходимости, обычно путем сравнивания приспособленности популяции на нескольких эпохах и остановки при стабилизации этого параметра. 3. Непрерывные генетические алгоритмы. Фиксированная длина хромосомы и кодирование строк двоичным алфавитом преобладали в теории генетических алгоритмов с момента начала ее развития, когда были получены ...
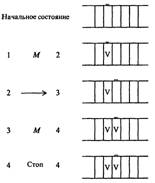
... в состояние qj, заменяя содержимое ячеек соответственно символами аb1 - аbк, то после этого ленты соответственно сдвигаются в направлениях k1... kk. До сих пор принималось, что различные алгоритмы осуществляются на различных машинах Тьюринга, отличающихся набором команд, внутренним и внешним алфавитами. Однако, можно построить универсальную машину Тьюринга, способную выполнять любой алгоритм ...
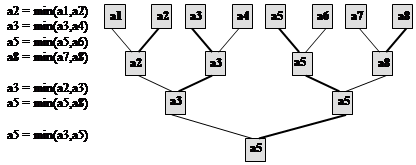
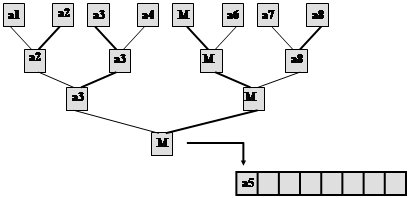
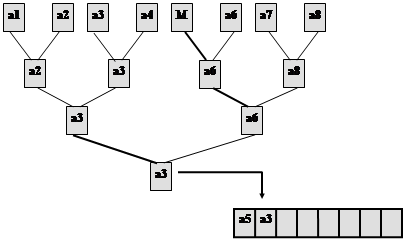
... M2(n) = O(l n), C2(n) = O(l n). Оскільки l = log2n, M2(n)=O(n log2 n)), C2(n)=O(n log2 n), Але З(n) = C1(n) + C2(n), M(n) = M1(n) + M2(n). Тому що C1(n) < C2(n), M1(n) < M2(n), остаточно одержуємо оцінки складності алгоритму TreeSort за часом: M(n) = O(n log2 n), C(n) = O(n log2 n), У загальному випадку, коли n не є ступенем 2, сортуюче дерево будується трохи інакше. “Зайвий” елемент ...
... U4 сравнения двух целых чисел оставляем читателю в качестве упражнения. Замечание: исходное слово надо задать в форме * Для нормальных алгоритмов Маркова справедлив тезис, аналогичный тезису Тьюринга. Тезис Маркова: Для любой интуитивно вычислимой функции существует алгоритм, ее вычисляющий. Построение алгоритмов из алгоритмов. До сих пор, строя ту или иную МТ, или НАМ мы каждый раз ...
0 комментариев