Необхідні поняття, факти і нотація із інших математичних дисциплін
Відношення і предикати
Коли <q; a1., am> – кінцевий стан, то
Аналгічно до класів KS-1 схем алгоритмів і ¶нтерпретацій KI-1 введемо, відпвидно, класи KS-2 і KI-2
Операторні та предикатні алгоритми -ІІ
Наслідок. Існує обчислювана функція h, для якої обидві проблеми «x Î Dom(h)» і «х Î Ran(h)» нерозв'язні
Теорема. Нехай c – довільне число. Наступні проблеми нерозв'язні
Логіка висловлень (пропозиційна логіка) [1] – одна з базових теорій математичної логіки, на якій базуються більш складні формальні логіки
Необхідно побудувати кон’юктивну нормальну форму для формули А логіки висловлень, де
Навигация
Відношення і предикати
Алгоритмічні проблеми
54576
знаков
5
таблиц
0
изображений
3. Відношення і предикати
Якщо А – множина, то властивість М(х1,…, хn), що виконується на деяких n-ках з Аn і не виконується (чи помилкове) на всіх інших n-ках з An, називається п-місним відношенням, чи предикатом на А.
Наприклад, властивість х<у є двомісне відношення (чи предикат) на N; 2 < 3 виконується (чи істинно), тоді як 9 < 5 не виконується (чи хибно). Інший приклад: кожна n-місна функція f з Nn у N приводить до (п + 1) – місцевого предиката М (х, у), що задається умовою:
М (x1,…, хn, у), якщо і тільки якщо f (x1,…, xn) 
у.
Відношення еквівалентності і порядку. (Читач, не знайомий з цими поняттями, може при бажанні відкласти читання цього параграфа доти, поки він не буде потрібен в гл. 9.) У гл. 9 ми зустрінемося із двома спеціальними видами відносин на множині А.
(a) Бінарне відношення R на множині А називається відношенням еквівалентності, якщо для всіх х, у, z
А виконуються три наступні властивості:
(i) (рефлективність) R (х, х);
(іі) (симетрія) R (х, y)
R (у, х);
(iii) (транзитивність) якщо R (x, y) і R (у, z), то R (х, z). Говорячи, що х, y еквівалентні (у деякому спеціальному змісті), ми маємо на увазі відношення R (х, у). Потім ми визначаємо клас еквівалентності х як множина {у | R (х, у)}, що складається з всіх елементів, еквівалентних х.
(b) Двомісне відношення R на множині А називається частковим порядком, якщо для всіх х, у, z A.
(i) (іррефлексивность) не R (х, х);
(іі) (транзитивність) якщо R (х, у) і R (y, z), те R (x, z).
Частковий порядок звичайно позначається символом <, і ми віддаємо перевагу запису х < у запису < (х, у). Часто визначають частковий порядок, вводячи спочатку предикат < (позначающий < чи =) із властивостями:
(i) х
х;
(ii) якщо xy і ух, те х=у;
(iii) відношення транзитивно, а потім визначаючи х < у як х у и х 
у.
4. Логічні позначення
Ми скрізь вживаємо стандартні логічні позначення. Символ 
позначає еквівалентність по визначенню, означає логічне слідування, а 
позначає «випливає з». Символи
, 
використовуються в значенні «для всіх» і «існує» відповідно.
3. Операторні та предикатні алгоритми – І
(Рекурсивні функції на області натуральних чисел N)
Розглянемо математичне визначення [1,2] класів функцій та предикатів, що вважаються точним аналогом інтуїтивного поняття алгоритму (взагалі кажучи, часткового).
1. Введемо зчисленні множини символів або послідовностей символів (слів, ідентифікаторів і т. п.) із довільної конструктивної множини:
а) індивідні: x, y, z, x0, y0, z0, x1, y1, z1,… xj, yj, zj,…;
б) функціональні: f, g, h, f0, g0, h0, f1, g1, h1,… fj, gj, hj,…;
в) предикатні: P, Q, R, P0, Q0, R0, P1, Q1, R1,… Pj, Qj, Rj,…;
г) константи: a, b, c, a0, b0, c0, a1, b1, c1,… aj, bj, cj,…;
д) мітки: q, i, j, q0, i0, j0, q1, i1, j1,… qk, ik, jk,…
Кожній функціональному та предикатному символу U однозначно ставиться у відповідність натуральне число n, яке називається арністю даного символа. Цей символ позначається через U(n), або U (x1, x2., xn) та т. п., і називається n-арним символом. Вважається, що ідеалізований об'єкт – 0-арний функціональний символ U(0) співпадає з символом константи.
Схемою оператора присвоювання називається вираз виду:
z(i) = f(m) (x(1)., x(m)). (1)
Схемою оператора пересилки називається вираз виду:
z(k) = y(j) (2)
Схемою прісвоювання константи називається вираз виду:
z(k) = a, або z(k) = fj(0) (3)
Схемою умови називається вираз виду:
P(s) (x(1)..x(s)) (4)
Схемою програми (СП) S називатимемо об'єкт виду
q0 Ф[0] (i0, j0)
q1 Ф[1] (i1, j1)
……………. (5)
qs Ф[s] (is, js)
В (1) Qs = Qs1 u Qs2, де Qs1 = q0, q1..qs, і
Qs2=i0, j0., is, js – підмножини множин міток. Як правило, якщо не вказане уточнення, будемо вважати, що qi – qj, якщо i – j, (qi, qj належать Q1). Мітки із Q1 називаються мітками передачі управління, а мітки із (Qs – Qs1) – кінцевими мітками.
Для всіх k є [0_s], Ф[k] – це одна із схем (1) – (4).
Сукупність всіх індивідних змінних СП (5) називається пам "яттю схеми S. Сукупність константанктних, функціональних, предикатних символів і пам" яті S називається сигнатурою, або базисом, схеми S.
Конструкція вигляду
qr Ф[r] (ir, jr)
із (5) називається схемою команди.
Схемою операторного алгоритму (СОА), або схемою операторної процедури, називається об"єкт виду:
SA = (x1, x2., xn; S; y), (6)
де x1., xn, y – змінні, S – СП вигляду (5).
Схемою предикатногоо алгоритму (СПА), або схемою предикатної процедури, називається об"єкт виду:
SP = (x1, x2., xn; S; q [.t.], q [.f.]), (7)
де x1., xn, – змінні, S – СП вигляду (5), а q [.t.], q [.f.]) – кінцеві мітки СП S.
Зауважимо, що пам "яттю алгоритмів (6), (7) називається об" єднання пам"ятті S і змінних x1., xn, y, і x1., xn називаються вхідними змінними, а y – вихідною змінною.
Ми визначили СП, СОА і СОП як деякі формальні, синтаксичні конструкції. Яка ж семантика (сенс) цих конструкцій? Як із них отримати справжні алгоритми (програми)?
Семантика схем задається за допомогою інтерпретацій. Інтерпретація схеми алгоритму W задається парою (D, I), де D – множина довільної природи, а I – це певне відображення, яке: а) кожному символу змінної z із пам"яті W ставить у відповідність елемент I(z) із множини D; б) кожному символу константи b із сигнатури W ставить у відповідність елемент I(b) із D; в) кожному m-арному функціональному f(m) (предикатному P(m)) символу співставляє, відповідно, всюдиозначені функцію I (f(m)): Dm ->D, або предикат I (P(m)) ->.t..f.
2. Нижче в данному розділі будемо розглядати тількі підклас схем алгоритмів KS-1, які містять тільки два функціональні унарні символи f, g, один константний символ b і один унарний предикатний символ p. Також обмежимо клас інтерпретацій, поклавши, що в цьому класі KI-1 D завжди співпадає з множиною натуральних чисел N (D=N), а відображення I задовольняє наступним вимогам:
1) I(b) = 0;
2) I (f(x)) = I(x) + 1;
I(x) – 1, коли x>0
3) I (g(x)) = I(x) -^ 1 =0 , коли x=0 (8)
t., коли I(x) =0;
4) I (p(x)) = P0 (x)) = *
f., коли I(x) > 0.
5) I(xi) єN для всіх вхідних змінних СОА і СПА виду (6), (7), і I(y) = 0 для всіх інших змінних із пам'яті вищезгаданих схем алгоритмів.
Опишемо формально функціонування алгоритму A виду (6).
Нехай M(A) = z1, z2..zn..zm – пам'ять алгоріму A, де zi = xi при 1<= i <= n, і zm = y. Через Q(A) позначимо всі мітки A. Станом пам'яті A будемо називати послідовність (a1..am) натуральних чисел, тобто елемент Nm. Станом (конфігурацією) алгоритму A будемо називати елемент <q; a1., am> із D(A) = Q & Nm.
Стан <q; a1., am> називається: а) проміжковим, якщо q – мітка передачи управління; б) кінцевим (заключним), якщо q – кінцева мітка алгоритму A.
Визначемо функцію переходів F: D(A) –> D(A) алгоритму A.
Похожие работы
... число эпох функционирования алгоритма, или определение его сходимости, обычно путем сравнивания приспособленности популяции на нескольких эпохах и остановки при стабилизации этого параметра. 3. Непрерывные генетические алгоритмы. Фиксированная длина хромосомы и кодирование строк двоичным алфавитом преобладали в теории генетических алгоритмов с момента начала ее развития, когда были получены ...
... в состояние qj, заменяя содержимое ячеек соответственно символами аb1 - аbк, то после этого ленты соответственно сдвигаются в направлениях k1... kk. До сих пор принималось, что различные алгоритмы осуществляются на различных машинах Тьюринга, отличающихся набором команд, внутренним и внешним алфавитами. Однако, можно построить универсальную машину Тьюринга, способную выполнять любой алгоритм ...
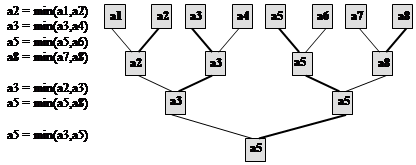
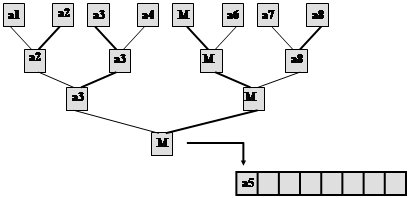
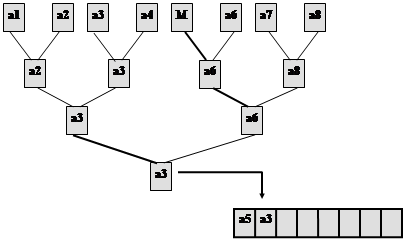
... M2(n) = O(l n), C2(n) = O(l n). Оскільки l = log2n, M2(n)=O(n log2 n)), C2(n)=O(n log2 n), Але З(n) = C1(n) + C2(n), M(n) = M1(n) + M2(n). Тому що C1(n) < C2(n), M1(n) < M2(n), остаточно одержуємо оцінки складності алгоритму TreeSort за часом: M(n) = O(n log2 n), C(n) = O(n log2 n), У загальному випадку, коли n не є ступенем 2, сортуюче дерево будується трохи інакше. “Зайвий” елемент ...
... U4 сравнения двух целых чисел оставляем читателю в качестве упражнения. Замечание: исходное слово надо задать в форме * Для нормальных алгоритмов Маркова справедлив тезис, аналогичный тезису Тьюринга. Тезис Маркова: Для любой интуитивно вычислимой функции существует алгоритм, ее вычисляющий. Построение алгоритмов из алгоритмов. До сих пор, строя ту или иную МТ, или НАМ мы каждый раз ...
0 комментариев