Навигация
Экономико – математическое моделирование прибыли ГУСП «Башхлебоптицепрома»
3.2 Экономико – математическое моделирование прибыли ГУСП «Башхлебоптицепрома»
В корреляционной матрице дается критическое значение коэффициента корреляции на уровне 90 % при двух степенях свободы:
уровень 90 % - это надежность получаемых результатов, она задается исследователем;
две степени свободы – это количество исследуемых одновременно параметров.
Все коэффициенты корреляции, табличные значения которых, меньше критического значения коэффициента корреляции (+ 0,2920), принимается равным нулю, то есть корреляционная связь между переменными является не значимой. Качественная оценка коэффициентов корреляции осуществляется на основе шкалы Чеддока.
Проанализируем силу связи зависимой переменной Y с независимыми переменными Хi.
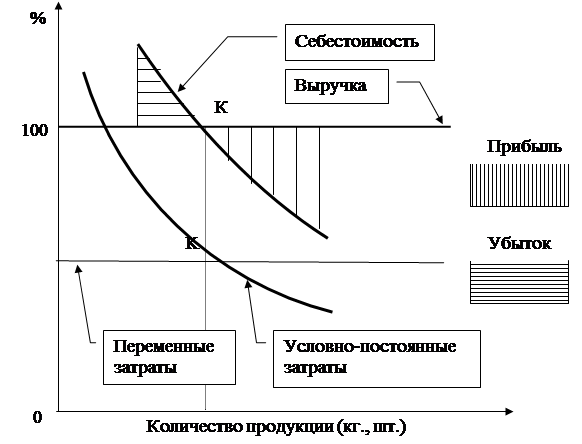
Целью данного исследования является построение «лучшей» модели для определения влияния составляющих затрат на изменение выручки от реализации товара на изменение прибыли, а также для прогноза прибыли на последующие 3 этапа, а именно на 3 месяца.
Для проведения исследования необходимы исходные данные. В данной задаче анализу подвергаются 7 составляющих затрат, с целью выявления их влияния на выручку от реализации товара.
Для проведения исследования по выявлению влияния составляющих затрат на выручку использовались данные бухгалтерского учета (журнал-ордер № , главная книга) ГУСП, представленные в таблице «Статистика данных по ГУСП «Башхлебоптицепрому» ( см. приложение № 5 ). В качестве исходных данных необходимых для проведения исследования выбираем статьи издержек обращения по 44 счету, наиболее значимые для расчета данного показателя с экономической точки зрения (см. приложение 5) .
Таблица с исходными данными состоит из столбцов и строк. По столбцам отражается временной интервал. В качестве периода исследования берем период по месяцам с июля 1998 года по март 2000 года. Этот временной интервал позволяет прогнозировать с достаточным количеством точек необходимым для получения адекватной модели с достаточной степенью точности. По строкам отражаются исследуемые переменные:Y – зависимая переменная, в нашем примере это показатель выпучки; Х – независимые переменные, а именно это:
Х1 – заработная плата;
Х2 – аммортизация основных средств;
Х3 – горюче-смазочные материалы;
Х4 – услуги охраны
Х5 – электро-энергия
Х6 – ремонтные работы
Х7 – запчасти
Все числовые данные представлены в тысячах рублей.
Прежде, чем построить модель, необходимо произвести предварительную обработку данных, которая включает в себя получение корреляционной матрицы (см. приложение 6).
Корреляционная матица есть квадратная матрица парных коэффициентов корреляции. Нумерация переменных соответствует приложению 5. Например, показатель 1 – это Y, показатель 2 - это Х1 и так далее.
Для проведения исследования взяты составляющие издержек обращения, а именно: заработная плата, амортизация основных средств, ГСМ, охрана, электро-энергия, ремонтные работы, запчасти для автомашин за отчетный период.
В качестве временного интервала для исследования взят период с июля 1998 года по март 2000 года., т.е. после кризисный период , когда произошли большие изменения в экономике страны, повлекшие за собой изменения в экономике и финансах предприятий. Для исследования данный период был взят для того, чтобы не было искажений и «скачков» в результатах, а также потому, что данный период имеет достаточное количество точек для получения адекватной модели .
Для проведения исследования составляющих выручки от реализации товара на прибыль применялись корреляционный и регрессионный анализ. Выполнение расчетов производилось с использованием стандартного программного продукта «СтатЭксперт . Исследование проводилось в 2 этапа:
Корреляционный анализ
Регрессионный анализ с прогнозом.
Корреляционный анализ:
Прежде чем построить модель необходимо провести предварительную обработку данных, которая включает в себя получение корреляционной матрицы исходных данных, используя коэффициенты парной корреляции. Результаты расчетов представлены в приложении 6.
Данная таблица есть корреляционная матрица, где по строкам и столбцам представлены исследуемые параметры, обозначенные как показатели 1,2,3,….11, нумерация которых соответствует порядку параметров, представленных в таблице , то есть показатель – 1 есть выручка, показатель 2 – заработная плата,….,показатель 8 – запчасти.
В корреляционной матрице дается критическое значение на уровне 90 % при 2-х степенях свободы равный 0,2920. Это означает, что надежность получаемых результатов в исследовании составляет 90 %, а две степени свободы – это количество исследуемых одновременно параметров. Критическое значение равное + 0,2920 используется для анализа таблицы . Коэффициенты корреляции , находящиеся в таблице , значение которых ниже 0,2920 (r ij< r i крит.) принимаются за величину равная нулю, то есть корреляционная связь между переменными считается не значимой или отсутствует.
На основании неравенства r ij< r i крит. корреляционная взаимосвязь отсутствует между следующими независимыми переменными (хi) с зависимыми переменными ( У- выручка). В регрессионном анализе данные показатели не учитываются.
Оценка коэффициентов корреляции осуществлялась на основе шкалы Чеддока:
Таблица 14
Шкала Чеддока
| № п/п | Критическое значение коэффициента | Показатель связи |
| 1 | 0,1 – 0,3 | слабая корреляционная связь |
Таблица 14
| 1 | 2 | 3 |
| 2 | 0,3 – 0,5 | умеренная корреляционная связь |
| 3 | 0,5 – 0,7 | заметная корреляционная связь |
| 4 | 0,7 – 0,9 | высокая корреляционная связь |
| 5 | 0,9 – 1,0 | весьма высокая корреляционная связь |
На основании шкалы Чеддока и данных Приложения 6 можно сказать о силе связи :
Между зависимой переменной с независимыми, а именно между выручкой и заработной платой, выручкой и амортизацией основных средств, связь слабая, а между выручкой и ГСМ, выручкой и ремонтом связь умеренная.
Между независимыми переменными, а именно между амортизацией основных средств и ГСМ связь весьма высокая, между заработной платой и амортизацией основных средств, заработной платой и ГСМ, заработной платой и электро-энергией, электро-энергией и амортизацией основных средств, ГСМ и электро-энергией высокая и т.д.
Следует сказать ,что связь между зависимой переменной с независимой показывает на сколько сильно влияет на выручку различные издержки обращения, а связь между независимыми переменными должна отсутствовать, так как ее наличие отрицательно сказывается на анализе. Если случайные величины связаны отрицательной корреляцией, это означает, что при возрастании одной случайной величины, другая имеет тенденцию в среднем убывать.
Таким образом, можно сделать вывод, что для построения регрессионной модели:
используются все выбранные вначале переменные;
влияние независимых переменных на финансовый результат значимо.
Регрессионный анализ с прогнозом :
Для построения регрессионной модели используется метод пошаговой регрессии, описанный в п.3.1 .
В результате использования метода пошаговой регрессии был отброшен 1 фактор и остались в таблице следующие независимые переменные: Х1, Х2, Х3, Х5, Х6, Х7. Таким образом, регрессионная модель будет иметь вид:
У = 9971,102 - 2,424Х1- 98,989Х2 + 123,384Х3 – 42,431Х5 + 3,592Х6 – - 63,342Х7, ( 32 )
где Х1 – заработная плата,
Х2 – амортизация основных средств,
Х3 – ГСМ,
Х5 – электро-энергия,
Х6 – ремонтные работы,
Х7 – запчасти.
Эти показатели наиболее оптимальные, они не коррелируют друг с другом и в совокупности образуют наилучшую модель Уравнение ( 32 ) означает, что сумма выручки на 1 руб. издержек по заработной плате в среднем по совокупности уменьшилась на 2,434 руб. при увеличении заработной платы на 1 руб.; уменьшилась в среднем на 97,989 руб. при возрастании амортизации основных средств на 1 руб. и уменьшилась на 42,431 руб. при росте электро-энергии и уменьшилась на 63,342 руб. при увеличении затрат на запчасти.
На основании коэффициентов регрессии bi трудно сопоставить факторы Х по степени их влияния на зависимую переменную У. Для этого используются следующие коэффициенты:
коэффициент эластичности ,Э ;
бэта-коэффициент, В ;
дельта-коэффициент, D;
С помощью частных коэффициентов эластичности, а также бета-коэффициентов можно ранжировать факторы по степени их влияния на зависимую переменную, сопоставить их между собой по величине этого влияния. Оценить долю влияния фактора в суммарном влиянии всех факторов на объясняемую переменную У можно с помощью дельта-коэффициент.
Оценка коэффициентов эластичности независимых переменных Х1, Х2, Х3, Х5, Х6, Х7 позволяет сделать вывод, что наибольшее влияние на изменение значений выручки оказывают издержки от амортизации основных средств: при увеличении амортизации основных средств на 1 % от среднего значения, выручка уменьшится на 0,471 % от своего среднего значения. При увеличении заработной платы на 1 % от среднего значения, выручка уменьшится на 0,211 % от своего значения. При увеличении электро-энергии на 1% от своего значения выручка уменьшится на 0,186% и при увеличении запчастей на 1% выручка уменьшится на 0,199%, что подтверждает выполненный ранее анализ уравнения.
Шесть факторов, включенные в уравнение регрессии, объясняют 100 % вариации уровня выручки (дельта-коэффициент), если рассматривать 7 составляющих издержек как генеральную совокупность. Наибольшие изменения вариации выручки происходит от амортизации основных ( -0,609%), а наименьшие изменения от ГСМ ( 0,295).
Таким образом, амортизация основных средств оказывает на уменьшение выручки предприятия наибольшее влияние.
Анализ качества регрессионной модели осуществляется по остаточной компоненте, которая определяется по формуле:
^
e=Ui- Yi , ( 33)
где e - i-ое значение остаточной компоненты
Yi– i-ое фактическое значение выручки
Yi – i-ое значение выручки, рассчитанной с помощью модели.
Среднее значение остаточной компоненты равна -0,005. Критерий Дарбина-Уотсона (d расч.) служит для проверки независимостей уровней. Расчетное значение критерия Дарбина-Уотсона (d расч.)= 1,698. При сравнении данного значения с табличным показателем мы видим:
d1 табл. (а = 0,05, р = 7, n = 17 ) = 0,90
d2 табл. (а = 0,05, р = 7, n = 17 ) = 1,71
Преобразуем d расч. : d расч.= 4 – 1,698 = 2,302 , то есть d расч. > d 2 табл.
Следовательно, автокорреляция уровней остаточного компонента отсутствует и остаточная компонента распределена по нормальному закону распределения.
Модель адекватна реальному процессу изменения прибыли в зависимости от увеличения заработной платы (Х1), аммортизации основных средств (Х2), ГСМ ( Х3), электро-энергия (Х5), ремонт (Х6), запчасти (Х7). Об этом свидетельствует высокий показатель критерия адекватности, который равен 89,495%.
Коэффициент детерминации показывает на сколько включенные в модель переменные влияют на изменение прибыль. В нашем случае, критерий детерминации равен 86,7%. Это означает, что переменные Х1,Х2,Х3,Х5,Х6,Х7 включенные в модель практически на 86,7 % описывают изменение . Данный факт подтверждается критерием Фишера (F-значение). F-значение (n1=6, n2= 14) равен 143,285. Это расчетное значение. Табличное же значение равно 8,74. Так как Fрасч. > F табл., то значение коэффициента детерминации значимо.
Таким образом, полученная в результате расчетов модель адекватна.
Критерий качества составляет лишь 22,374%. Это свидетельствует о низком качестве оценок.
В результате проведенного выше анализа можно сказать, что уравнение (32) значимо с вероятностью 0,95 и может быть применено для получения прогноза прибыли.
Прогнозные значения выручки на ближайшие 3 месяца (апрель- май-июнь 2000 г.) представлены в графике. Для наглядного представления изменения выручки были и описания этого изменения с помощью модели, а также прогнозные значения выручки Приложении 9 представлены на рисунке .
Анализируя данные рисунка , мы видим, что в апреле 1999 года, произошло снижение выручки, когда выросли заработная плата, амортизация основных средств в 2 раза. В декабре 1999 года сумма выручки выросла и достигла наибольшего роста, но в январе 2000 года снизился до минимума. Однако, в феврале 2000 года показатель выручки опять стал расти. Прогнозное значение прибыли на ближайшие 3 месяца (апрель - июнь 2000г.) снижается .В апреле 2000 года ожидается снижение прибыли с 21772 до 1535,496 руб. (или на 7,05%). В мае 2000 года по сравнению с апрелем 2000г. показатель выручки уменьшится на 324,07% (-4976,136 / 1535,496 * 100). А в июне ожидается увеличение показателя выручки с –4976,136 до 10896,939 руб. или на 218,98%.
Таким образом, на основании проведенных исследований можно сделать следующие выводы :
Корреляционная связь зависимой переменной У (выручка) с независимыми переменными Хi изменяется от умеренной (Х3 – ГСМ, Х6- ремонт) до слабой (Х1- заработная плата, Х2- амортизация основных средств). В тоже время следует сказать ,что связь между независимыми переменными должна отсутствовать, так как ее наличие отрицательно сказывается на анализе. Если случайные величины связаны отрицательной корреляцией, это означает, что при возрастании одной случайной величины, другая имеет тенденцию в среднем убывать.
Взаимное влияние независимых переменных не значимо, то есть мультиколлениарность отсутствует.
В результате расчетов получена регрессионная модель зависимости выручки от заработной платы, амортизации основных средств, ГСМ, электро –
нергии, ремонта, запчастей. Она имеет вид :
У = 9971,102 – 2,434 Х1 – 97,989 Х2 + 123,384 Х3 – 42,431Х5 + 3,592Х6 – - 63,342Х7
Модель имеет среднее качество и может с вероятностью 0,95 применена для прогнозирования значений прибыли.
Включенные в модель регрессии переменные Х1 (заработная плата), Х2 (амортизация основных средств), Х3 (ГСМ), Х5 (электро-энергия), Х6 (ремонт), Х7 (запчасти) на 89,495% описывают изменения выручки. Наибольшее влияние на изменение выручки оказывает амортизация основных средств ( на основании анализа дельта-коэффициента ).
Прогноз прибыли предполагает его дальнейшее снижение.
ГЛАВА 4. МЕРОПРИЯТИЯ ПО УЛУЧШЕНИЮ ФИНАНСОВЫХ РЕЗУЛЬТАТОВ ДЕЯТЕЛЬНОСТИ ГУСП «БАХЛЕБОПТИЦЕПРОМ”
Похожие работы
... продукции для столицы Беларуси. На предприятии внедрены передовые технологии и высокопроизводительное оборудование ведущих отечественных и зарубежных фирм, которые позволяют добиваться высоких производственных показателей. 2. ОРГАНИЗАЦИЯ УЧЕТА И КОНТРОЛЯ РЕАЛИЗАЦИИ ГОТОВОЙ ПРОДУКЦИИ 2.1. Документальное оформление операций по реализации готовой продукции Первичный учет представляет собой ...
... прибыли от реализации продукции и снижение себестоимости товарной продукции. На основе изученного теоретического материала проведем анализ финансовых результатов деятельности ООО «Евролот Запад». 2. АНАЛИЗ ФИНАНСОВЫХ РЕЗУЛЬТАТОВ ДЕЯТЕЛЬНОСТИ ООО «ЕВРОЛОТ-ЗАПАД» 2.1 Организационно-правовая и экономическая характеристика предприятия Предприятие ООО «Евролот Запад» создано по решению ...
... лиц – уменьшилась с 18,6 до 18,3 %. Также незначительно изменилась доля сбора на уборку и благоустройство города с 12,4 до 12,2% соответственно. По проведенному анализу можно сделать вывод, что доля налогов, влияющих на прибыль и относимых на финансовый результат сократилась в 2000г. по сравнению с 1999г. 3. МЕРОПРИЯТИЯ ПО СОВЕРШЕНСТВОВАНИЮ УПРАВЛЕНИЯ ПРИБЫЛЬЮ ПРЕДПРИЯТИЯ ОАО МОЛЗАВОД « ...
... заключение о достаточно эффективной организации бухгалтерского учета в ООО "Интел - плюс", отвечающее требованиям достоверности, полноты, адекватности. 2 АНАЛИЗ ФИНАНСОВОГО РЕЗУЛЬТАТА В ООО "ИНТЕЛ-ПЛЮС" 2.1 Организация учета финансового результата в ООО "Интел - плюс" Правила формирования в бухгалтерском учете ООО "Интел - плюс" информации о доходах определяются в соответствии с Положением ...

0 комментариев