Навигация
Процедура статистической идентификации
3.3 Процедура статистической идентификации.
В качестве решающего правила используются алгоритмы идентификации, основанные на классических статистических дискриминаторах, таких как линейный и квадратичный дискриминаторы. Данные алгоритмы применяются наиболее часто в виду простоты их использования, удобства обучения применительно к конкретному региону и легкости оценивания вероятности ошибочной идентификации взрывов и землетрясений для каждого конкретного региона Их роль как эффективных правил выбора решения при идентификации особенно возрастает, если применять эти алгоритмы к множествам обучающих и идентифицируемых векторов, составленных из наиболее информативных для данного региона дискриминантных признаков, отобранных в соответствии с описанной выше методикой.
Линейная дискриминантная функция описывается следующей формулой
![]() . (8)
. (8)
где k - число отобранных наиболее информативных признаков, x(k) - классифицируемый вектор, m(k,1), m(k,2) - k - мерные векторы выборочных средних, вычисленные по k-мерным векторам x1j(k) jÎ1,n1 и x2j(k) jÎ1,n2 1го и 2-го классов, S-1n1+n2(k) - (k´k)- мерная обратная выборочная матрица ковариаций, вычисленная с использованием всего набора k - мерных векторов x1j(k) jÎ1,n1 и x2j(k) jÎ1,n2. Если LDF > 0, то принимается, что вектор x(k) принадлежит первому классу - (землетрясение); в противоположном случае он принадлежит второму класс (взрыв).
Квадратичная дискриминационная функция описывается следующей формулой
![]() (9)
(9)
где ![]() , s=1,2 - обратные матрицы ковариаций обучающих выборок 1-го и 2-го классов, вычисленные по обучающим векторам x1j(k) jÎ1,n1 и x2j(k) jÎ1,n2, соответственно.
, s=1,2 - обратные матрицы ковариаций обучающих выборок 1-го и 2-го классов, вычисленные по обучающим векторам x1j(k) jÎ1,n1 и x2j(k) jÎ1,n2, соответственно.
3.4 Оценка вероятности ошибочной классификации методом скользящего экзамена.
Оценивание вероятности ошибочной идентификации типа событий (землетрясение-взрыв), в каждом конкретном регионе представляет собой одну из основных практических задач мониторинга. Эту задачу приходится решать на основании накопления региональных сейсмограмм событий, о которых доподлинно известно, что они порождены землетрясениями или взрывами. Эти же сейсмограммы представляют собой "обучающие данные" для адаптации решающих правил.
Из теории распознавания образов известно, что наиболее точной и универсальной оценкой вероятности ошибок классификации является оценка, обеспечиваемая процедурой “скользящего экзамена”(“cross-validation”) [11].
В методе скользящего экзамена на каждом шаге один из обучающих векторов xsj , jÎ1,ns, sÎ1,2, исключается из обучающей выборки. Оставшиеся векторы используются для адаптации (обучения) LDF или QDF или любого другого дискриминатора. Исключенный вектор затем классифицируется с помощью дискриминатора, обученного без его участия. Если этот вектор классифицируется неправильно, т.е. относится к классу 2 вместо класса 1 или наоборот, соответствующие “счетчики” n12 или n21 увеличиваются на 1. Исключенный вектор затем возвращается в обучающую выборку, а изымается уже другой вектор xs(j+1). Процедура повторяется для всех nl +n2 обучающих векторов. Вычисляемая в результате величина
p0=(n12 +n21)/( nl +n2 )
является состоятельной оценкой полной вероятности ошибочной классификации. Значения дискриминатора, полученные в результате процедуры скользящего экзамена для обоих классов, ранжируются по амплитуде: ранжированные последовательности удобнее сравнивать с порогом и делать выводы о “физических” причинах ошибочной классификации.
4. Обзор различных архитектур нейронных сетей, предназначенных для задач классификации.
Приступая к разработке нейросетевого решения, как правило, сталкиваешься с проблемой выбора оптимальной архитектуры нейронной сети. Так как области применения наиболее известных парадигм пересекаются, то для решения конкретной задачи можно использовать совершенно различные типы нейронных сетей, и при этом результаты могут оказаться одинаковыми. Будет ли та или иная сеть лучше и практичнее, зависит в большинстве случаев от условий задачи. Так что для выбора лучшей приходится проводить многочисленные детальные исследования.
Рассмотрим ряд основных парадигм нейронных сетей, успешно применяемых для решения задачи классификации, одна из постановок которой представлена в данной дипломной работе.
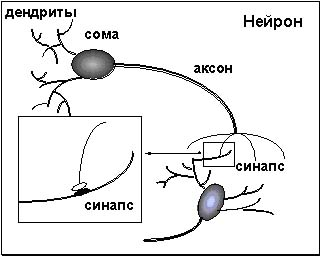
4.1 Нейрон – классификатор.
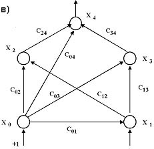
Простейшим устройством распознавания образов в нейроинформатике является одиночный нейрон (рис. 4.1), превращающий входной вектор признаков в скалярный ответ, зависящий от линейной комбинации входных переменных [1-5, 7,10]:
 | |||
Скалярный выход нейрона можно использовать в качестве т.н. дискриминантной функции. Этим термином называют индикатор принадлежности входного вектора к одному из заданных классов, а нейрон соответственно – линейным дискриминатором. Так, если входные вектора могут принадлежать одному из двух классов, можно различить тип входа, например, следующим образом: если f(x) ³ 0, входной вектор принадлежит первому классу, в противном случае – второму. Рассмотрим алгоритм обучения подобной структуры, приняв f(x)ºx.
Итак, в p-мерном пространстве задана обучающая выборка x1,…,xn (первый класс) и y1,…,ym (второй класс). Требуется найти такие p+1-мерный вектор w, что для всех i=1,…,n и j=1,…,m w0+(xi,w)>0 и w0+(yj,w)<0.
Переформулируем задачу, сведя ее к отделению нуля от конечного множества векторов в p+1 - мерном пространстве. Для этого рассмотрим p+1 – мерные векторы zl (l=0, 1,…., n+m):
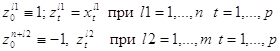
В этих обозначениях условия разделения превращаются в систему n+m однотипных неравенств:
![]()
В качестве нулевого приближения можно выбрать любой вектор w, например, w=0, или wÍR[-0.5,0.5]. Цикл алгоритма состоит в том, что для всех l = 1,…,n+m проверяется неравенство (zl,w) > 0. Если для данного l £ n+m оно выполнено, переходим к следующем l (либо при l=n+m заканчиваем цикл), если же не выполнено, то модифицируем w по правилу w=w+zl , или w=w+hTzl, где T – номер модификации, а ![]() , например.
, например.
Когда за весь цикл нет ни одной ошибки ( т.е. модификации w), то решение w найдено, в случае же ошибок полагаем l=1 и снова проходим цикл.
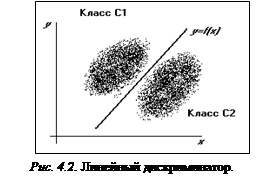
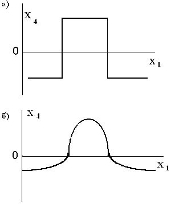
В некоторых простейших случаях линейный дискриминатор – наилучший из возможных, а именно когда оба класса можно точно разделить одной гиперплоскостью, рисунок 4.2 демонстрирует эту ситуацию для плоскости, когда p=2.
Похожие работы
... МП к некритическому экстраполированию результата считается его слабостью. Сети РБФ более чувствительны к «проклятию размерности» и испытывают значительные трудности, когда число входов велико. 5. МОДЕЛИРОВАНИЕ НЕЙРОННЫХ СЕТЕЙ ДЛЯ ПРОГНОЗИРОВАНИЯ СТОИМОСТИ НЕДВИЖИМОСТИ 5.1 Особенности нейросетевого прогнозирования в задаче оценки стоимости недвижимости Использование нейронных сетей можно ...
... в связи с необходимостью упорядоченного сообщения с высоким приоритетом при радикальном изменении окружающих условий и двунаправленностью каналов. Возможности вычисления путей маршрутизации можно применять при построении интегральных схем и проектирования кристаллов процессоров. Нейрокомпьютеры с успехом применяются при обработке сейсмических сигналов в военных целях для определения коорди
... (ШД), адресов (ША) и управления (ШУ). Однокристальные микропроцессоры получаются при реализации всех аппаратных средств процессора в виде одной БИС или СБИС (сверхбольшой интегральной схемы). По мере увеличения степени интеграции элементов в кристалле и числа выводов корпуса параметры однокристальных микропроцессоров улучшаются. Однако возможности однокристальных микропроцессоров ограничены ...
... данных а разбивать входные данные на кластеры. •Рекурсивные сети Элмана, способные обрабатывать последовательности векторов. •Вероятностные сети, аппроксимирующие Байесовские классификаторы с любой степенью точности. Общие принципы, характерные для нейросетей Согласно общепринятым представлениям наиболее общими принципами, характерными для современных нейросетей являются: коннекционизм, ...

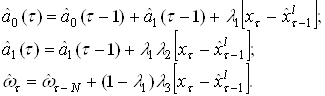


0 комментариев