Выводы по разделу

4.5 Выводы по разделу.

Итак, подводя итог данной главе, следует сказать, что это далеко не полный обзор нейросетевых архитектур, которые успешно справляются с задачами классификации. В частности ничего не было сказано о вероятностных нейронных сетях, о сетях с базисно радиальными функциями, о использовании генетических алгоритмов для настройки многослойных сетей и о других, пусть менее известных, но хорошо себя зарекомендовавших. Соответственно проблема выбора наиболее оптимальной архитектуры для решения задачи классификации сейсмических сигналов вполне актуальна. В идеале, конечно хотелось бы проверить эффективность хотя бы нескольких из них и выбрать наилучшую. Но для этого необходимо проводить более масштабные исследования, которые займут много времени. На данном этапе исследований была сделана попытка использовать хорошо изученные нейронные сети и алгоритмы обучения для того, чтобы убедиться в эффективности подхода в целом. В главе 6 детально обсуждаются нейросеть, которая была исследована в рамках настоящей дипломной работы.

Если возникает необходимость использовать нейросетевые методы для решения конкретных задач, то первое с чем приходится сталкиваться – это подготовка данных. Как правило, при описании различных нейроархитектур, по умолчанию предполагают что данные для обучения уже имеются и представлены в виде, доступном для нейросети. На практике же именно этап предобработки может стать наиболее трудоемким элементом нейросетевого анализа. Успех обучения нейросети также может решающим образом зависеть от того, в каком виде представлена информация для ее обучения.

В этой главе рассматриваются различные процедуры нормировки и методы понижения размерности исходных данных, позволяющие увеличить информативность обучающей выборки.

5.1 Максимизация энтропии как цель предобработки.

Рассмотрим основной руководящий принцип, общий для всех этапов предобработки данных. Допустим, что в исходные данные представлены в числовой форме и после соответствующей нормировки все входные и выходные переменные отображаются в единичном кубе. Задача нейросетевого моделирования – найти статистически достоверные зависимости между входными и выходными переменными. Единственным источником информации для статистического моделирования являются примеры из обучающей выборки. Чем больше бит информации принесет пример – тем лучше используются имеющиеся в нашем распоряжении данные.

Рассмотрим произвольную компоненту нормированных (предобработанных) данных: . Среднее количество информации, приносимой каждым примером , равно энтропии распределения значений этой компоненты . Если эти значения сосредоточены в относительно небольшой области единичного интервала, информационное содержание такой компоненты мало. В пределе нулевой энтропии, когда все значения переменной совпадают, эта переменная не несет никакой информации. Напротив, если значения переменной  равномерно распределены в единичном интервале, информация такой переменной максимальна.

Общий принцип предобработки данных для обучения, таким образом состоит в максимизации энтропии входов и выходов.

5.2 Нормировка данных.

Как входами, так и выходами могут быть совершенно разнородные величины. Очевидно, что результаты нейросетевого моделирования не должны зависеть от единиц измерения этих величин. А именно, чтобы сеть трактовала их значения единообразно, все входные и выходные величин должны быть приведены к единому масштабу. Кроме того, для повышения скорости и качества обучения полезно провести дополнительную предобработку, выравнивающую распределения значений еще до этапа обучения.

Индивидуальная нормировка данных.

Приведение к единому масштабу обеспечивается нормировкой каждой переменной на диапазон разброса ее значений. В простейшем варианте это – линейное преобразование:

в единичный отрезок: . Обобщение для отображения данных в интервал , рекомендуемого для входных данных тривиально.

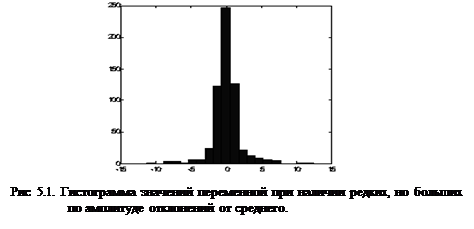
Линейная нормировка оптимальна, когда значения переменной  плотно заполняют определенный интервал. Но подобный «прямолинейный» подход применим далеко не всегда. Так, если в данных имеются относительно редкие выбросы, намного превышающие типичный разброс, именно эти выбросы определят согласно предыдущей формуле масштаб нормировки. Это приведет к тому, что основная масса значений нормированной переменной  сосредоточится вблизи нуля  Гораздо надежнее, поэтому, ориентироваться при нормировке не а экстремальные значения, а на типичные, т.е. статистические характеристики данных, такие как среднее и дисперсия.

, где

,

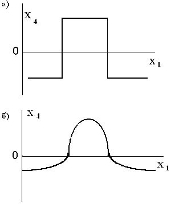
В этом случае основная масса данных будет иметь единичный масштаб, т.е. типичные значения все переменных будут сравнимы (рис. 6.1)

Однако, теперь нормированные величины не принадлежат гарантированно единичному интервалу, более того, максимальный разброс значений  заранее не известен. Для входных данных это может быть и не важно, но выходные переменные будут использоваться в качестве эталонов для выходных нейронов. В случае, если выходные нейроны – сигмоидные, они могут принимать значения лишь в единичном диапазоне. Чтобы установить соответствие между обучающей выборкой и нейросетью в этом случае необходимо ограничить диапазон изменения переменных.

Линейное преобразование, представленное выше, не способно отнормировать основную массу данных и одновременно ограничить диапазон возможных значений этих данных. Естественный выход из этой ситуации – использовать для предобработки данных функцию активации тех же нейронов. Например, нелинейное преобразование

,

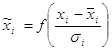нормирует основную массу данных одновременно гарантируя что (рис. 5.2)

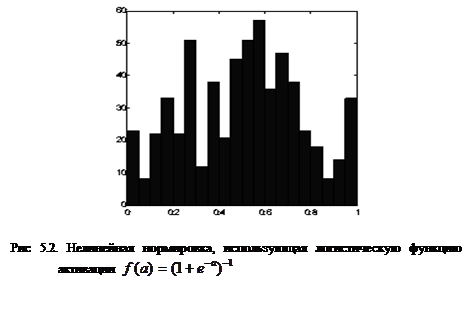
Как видно из приведенного выше рисунка, распределение значений после такого нелинейного преобразования гораздо ближе к равномерному.

Все выше перечисленные методы нормировки направлены на то, чтобы максимизировать энтропию каждого входа (выхода) по отдельности. Но, вообще говоря, можно добиться гораздо большего максимизируя их совместную энтропию. Существуют методы, позволяющие проводить нормировку для всей совокупности входов, описание некоторых из них приведено в [4].

Похожие работы

Анализ методов прогнозирования и моделирование нейронных сетей для прогнозирования стоимости недвижимости

Скачать

110516

5

18

... МП к некритическому экстраполированию результата считается его слабостью. Сети РБФ более чувствительны к «проклятию размерности» и испытывают значительные трудности, когда число входов велико. 5. МОДЕЛИРОВАНИЕ НЕЙРОННЫХ СЕТЕЙ ДЛЯ ПРОГНОЗИРОВАНИЯ СТОИМОСТИ НЕДВИЖИМОСТИ   5.1 Особенности нейросетевого прогнозирования в задаче оценки стоимости недвижимости Использование нейронных сетей можно ...

Рынок военных нейрокомпьютеров

Скачать

15022

0

0

... в связи с необходимостью упорядоченного сообщения с высоким приоритетом при радикальном изменении окружающих условий и двунаправленностью каналов. Возможности вычисления путей маршрутизации можно применять при построении интегральных схем и проектирования кристаллов процессоров. Нейрокомпьютеры с успехом применяются при обработке сейсмических сигналов в военных целях для определения коорди

Сверхбольшие интегральные схемы

Скачать

84679

0

11

... (ШД), адресов (ША) и управления (ШУ). Однокристальные микропроцессоры получаются при реализации всех аппаратных средств процессора в виде одной БИС или СБИС (сверхбольшой интегральной схемы). По мере увеличения степени интеграции элементов в кристалле и числа выводов корпуса параметры однокристальных микропроцессоров улучшаются. Однако возможности однокристальных микропроцессоров ограничены ...

Общие принципы, характерные для нейросетей

Скачать

20016

0

6

... данных а разбивать входные данные на кластеры. •Рекурсивные сети Элмана, способные обрабатывать последовательности векторов. •Вероятностные сети, аппроксимирующие Байесовские классификаторы с любой степенью точности.   Общие принципы, характерные для нейросетей Согласно общепринятым представлениям наиболее общими принципами, характерными для современных нейросетей являются: коннекционизм, ...