Навигация
Многослойный персептрон
4.2 Многослойный персептрон.
Возможности линейного дискриминатора весьма ограничены. Для решения более сложных классификационных задач необходимо усложнить сеть вводя дополнительные (скрытые) слои нейронов, производящих промежуточную предобработку входных данных, таким образом, чтобы выходной нейрон-классификатор получал на свои входы уже линейно-разделимые множества. Такие структуры носят название многослойные персептроны [1-4,7,10] (рис. 1.3).
Легко показать, что, в принципе, всегда можно обойтись одним скрытым слоем, содержащим, достаточно большое число нейронов. Действительно, увеличение скрытого слоя повышает размерность пространства, в котором выходной нейрон производит классификацию, что, соответственно, облегчает его задачу.
Персептроны весьма популярны в нейроинформатике. И это обусловлено, в первую очередь, широким кругом доступных им задач, в том числе и задач классификации, распознавания образов, фильтрации шумов, предсказание временных рядов, и т.д., причем применение именно этой архитектуры в ряде случаев вполне оправдано, с точки зрения эффективности решения задачи.
Рассмотрим какие алгоритмы обучения многослойных сетей разработаны и применяются в настоящее время.[7,10]. В основном все алгоритмы можно разбить на две категории:
· Градиентные алгоритмы;
· Стохастические алгоритмы.
К первой группе относятся те, которые основаны на вычислении производной функции ошибки и корректировке весов в соответствии со значением найденной производной. Каждый дальнейший шаг направлен в сторону антиградиента функции ошибки. Основу всех этих алгоритмов составляет хорошо известный алгоритм обратного распространения ошибки (back propagation error).[1-5,7,10].
![]() ,где функция ошибки
,где функция ошибки ![]()
Многочисленные модификации, разработанные в последнее время, позволяют существенно повысить эффективность этого алгоритма. Из них наиболее известными являются:
1. Обучение с моментом.[4,7]. Идея метода заключается в добавлении к величине коррекции веса значения пропорционального величине предыдущего изменения этого же весового коэффициента.
![]()
2. Автономный градиентный алгоритм (Обучение с автоматическим изменением длины шага h). [10]
3. RPROP (от resilient –эластичный), в котором каждый вес имеет свой адаптивно настраиваемый темп обучения.[4]
4. Методы второго порядка, которые используют не только информацию о градиенте функции ошибки, но и информацию о вторых производных .[3,4,7].
Стохастические методы обучения выполняют псевдослучайные изменения величин весов, сохраняя те изменения, которые ведут к улучшениям характеристик сети. К этой группе алгоритмов относятся такие как
1. Алгоритм поиска в случайном направлении.[10]
2. Больцмановское обучение или (алгоритм имитации отжига). [1]
3. Обучение Коши, как дополнение к Больцмановскому обучению.[1]
Основным недостатком этой группы алгоритмов является очень долгое время обучения, а соответственно и большие вычислительные затраты. Однако, как пишут в различных источниках, эти алгоритмы обеспечивают глобальную оптимизацию, в то время как градиентные методы в большинстве случаев позволяют найти только локальные минимумы функционала ошибки.
Известны также алгоритмы, которые основаны на совместном использовании обратного распространения и обучения Коши. Коррекция весов в таком комбинированном алгоритме состоит из двух компонент: направленной компоненты, вычисляемой с использованием алгоритма обратного распространения, и случайной компоненты, определяемой распределением Коши. Однако, несмотря на хорошие результаты, эти методы еще плохо исследованы.
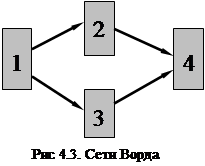
4.3 Сети Ворда.
Одним из вариантов многослойного персептрона являются нейронные сети Ворда. Они способны выделять различные свойства в данных, благодаря наличию в скрытом слое нескольких блоков, каждый из которых имеет свою передаточную функцию (рис.4.4). Передаточные функции (обычно сигмоидного типа) служат для преобразования внутренней активности нейрона. Когда в разных блоках скрытого слоя используются разные передаточные функции, нейросеть оказывается способной выявлять новые свойства в предъявляемом образе. Для настройки весовых коэффициентов используются те же алгоритмы, о которых говорилось в предыдущем разделе.
4.2 Сети Кохонена.
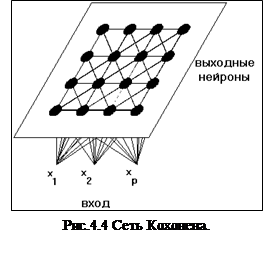
Сети Кохонена – это одна из разновидностей нейронных сетей, для настройки которой используется алгоритм обучения без учителя. Задачей нейросети Кохонена является построение отображения набора входных векторов высокой размерности на карту кластеров меньшей размерности , причем таким образом, что близким кластерам на карте отвечают близкие друг к другу входные векторы в исходном пространстве.
Сеть состоит из M нейронов, образующих, как правило одномерную или двумерную карту (рис. 4.2). Элементы входных сигналов {xi} подаются на входы всех нейронов сети. В процессе функционирования (самоорганизации) на выходе слоя Кохонена формируются кластеры (группа активных нейронов определённой размерности, выход которых отличен от нуля), характеризующие определённые категории входных векторов (группы входных векторов, соответствующие одной входной ситуации). [9]
Алгоритм Кохонена формирования карт признаков.
Шаг 1. Инициализировать веса случайными значениями. Задать размер окрестности s(0), и скорость h(0) и tmax.
Шаг 2. Задать значения входных сигналов (x1,…,xp).
Шаг 3. Вычислить расстояние до всех нейронов сети. Расстояния dk от входного сигнала x до каждого нейрона k определяется по формуле:
![]()
где
xi - i-ый элемент входного сигнала,
wki - вес связи от i-го элемента входного сигнала к нейрону k.
Шаг 4. Найти нейрон – победитель, т.е. найти нейрон j, для которого расстояние dj наименьшее:
j:dj < dk "k¹p
Шаг 5. Подстроить веса победителей и его соседей.
![]()
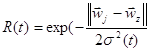
Шаг 6. Обновить размер окрестности s(t) и скорость h(t)
s(t)=s(0)(1-t/tmax) h(t)=h(0)(1-t/tmax)
Шаг 7. Если (t < tmax), то Шаг 2, иначе СТОП.
Благодаря своим способностям к обобщению информации, карты Кохонена являются удобным инструментом для наглядного представления о структуре данных в многомерном входном пространстве, геометрию которого представить практически невозможно.
Сети встречного распространения.
Еще одна группа технических применений связана с предобработкой данных. Карта Кохонена группирует близкие входные сигналы Х, а требуемая функция Y = G(X) строится на основе обычной нейросети прямого распространения (например многослойного персептрона или линейной звезды Гроссберга[1]) к выходам нейронов Кохонена. Такая гибридная архитектура была предложена Р. Хехт-Нильсеном и имеет название сети встречного распространения[1-3,7,9]. Нейроны слоя Кохонена обучаются без учителя, на основе самоорганизации, а нейроны распознающих слоев адаптируются с учителем итерационными методами. Пример такой структуры для решения задачи классификации сейсмических сигналов приведен на рис. 4.5.
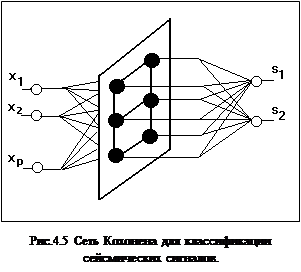
Второй уровень нейросети используется для кодирования информации. Весовые коэффициенты tij (i =1,...,M; j=1,2) – коэффициенты от i-го нейрона слоя Кохонена к j-му нейрону выходного слоя рассчитываются следующим образом:
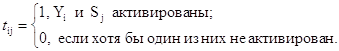
где
Yi – выход i- го нейрона слоя Кохонена
Sj – компонента целевого вектора (S={0,1} – взрыв, S={1,0}-землетрясение)
Таким образом после предварительного обучения и формирования кластеров в слое Кохонена, на фазе вторичного обучения все нейроны каждого полученного кластера соединяются активными (единичными) синапсами со своим выходным нейроном, характеризующим данный кластер.
Выход нейронов второго слоя определяется выражением:
(11) 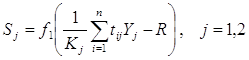
где: ![]()
Kj - размерность j-ого кластера, т.е. количество нейронов слоя Кохонена соединённых с нейроном j выходного слоя отличными от нуля коэффициентами.
R - пороговое значение (0 < R < 1).
Пороговое значение R можно выбрать таким образом, чтобы с одной стороны не были потеряны значения активированных кластеров, а с другой стороны - отсекался "шум не активизированных кластеров".
В результате на каждом шаге обработки исходных данных на выходе получаются значения Sj, которые характеризуют явление, породившее данную входную ситуацию (![]() - землетрясение;
- землетрясение; ![]() - взрыв).
- взрыв).
Похожие работы
... МП к некритическому экстраполированию результата считается его слабостью. Сети РБФ более чувствительны к «проклятию размерности» и испытывают значительные трудности, когда число входов велико. 5. МОДЕЛИРОВАНИЕ НЕЙРОННЫХ СЕТЕЙ ДЛЯ ПРОГНОЗИРОВАНИЯ СТОИМОСТИ НЕДВИЖИМОСТИ 5.1 Особенности нейросетевого прогнозирования в задаче оценки стоимости недвижимости Использование нейронных сетей можно ...
... в связи с необходимостью упорядоченного сообщения с высоким приоритетом при радикальном изменении окружающих условий и двунаправленностью каналов. Возможности вычисления путей маршрутизации можно применять при построении интегральных схем и проектирования кристаллов процессоров. Нейрокомпьютеры с успехом применяются при обработке сейсмических сигналов в военных целях для определения коорди
... (ШД), адресов (ША) и управления (ШУ). Однокристальные микропроцессоры получаются при реализации всех аппаратных средств процессора в виде одной БИС или СБИС (сверхбольшой интегральной схемы). По мере увеличения степени интеграции элементов в кристалле и числа выводов корпуса параметры однокристальных микропроцессоров улучшаются. Однако возможности однокристальных микропроцессоров ограничены ...
... данных а разбивать входные данные на кластеры. •Рекурсивные сети Элмана, способные обрабатывать последовательности векторов. •Вероятностные сети, аппроксимирующие Байесовские классификаторы с любой степенью точности. Общие принципы, характерные для нейросетей Согласно общепринятым представлениям наиболее общими принципами, характерными для современных нейросетей являются: коннекционизм, ...

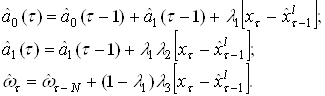


0 комментариев