Навигация
Разложение дробной рациональной функции на простейшие дроби
5. Разложение дробной рациональной функции на простейшие дроби.
Рациональной дробью R(x) называется дробь, числителем и знаменателем которой являются многочлены, т. Е. всякая дробь вида:
![]()
Если степень многочлена в числителе больше или равна степени многочлена в знаменателе (n≥m), то дробь называется неправильной. Если степень многочлена в числителе меньше степени многочлена в знаменателе (n≤m), то дробь называется правильной.
Всякую неправильную рациональную дробь можно представить в виде суммы многочлена (целой части) и правильной рациональной дроби (это представление достигается путем деления числителя на знаменатель по правилу деления многочленов):
![]()
где R(x) – многочлен-частное (целая часть) дроби ![]() ; Pn(x) – остаток (многочлен степени n < m).
; Pn(x) – остаток (многочлен степени n < m).
6. Интегрирование простейших дробей. Интегрирование рациональных дробей.
Интегрирование простейших дробей. Простейшей дробью называется правильная рациональная дробь одного из следующих четырех типов:
1) ![]()
2) ![]() (n≥2);
(n≥2);
3) ![]()
4) ![]() (n≥2).
(n≥2).
Здесь А, a, p, q, M, N – действительные числа, а трехчлен не имеет действительных корней, т. е. p2/4-q < 0.
Простейшие дроби первого и второго типов интегрируются непосредственно с помощью основных правил интегрального исчисления:
![]()
![]()
Интеграл от простейшей дроби третьего типа приводится к табличным интегралам путем выделения в числителе дифференциала знаменателя и приведения знаменателя к сумме квадратов:
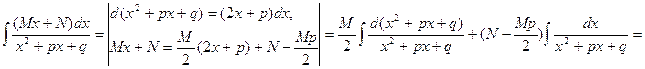
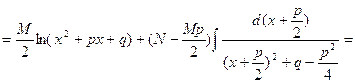
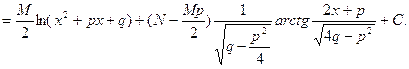
Интегрирование рациональных дробей.
Разложение рациональной дроби на простейшие дроби. Всякую правильную рациональную дробь ![]() можно представить в виде суммы конечного числа простейших рациональных дробей первого – четвертого типов. Для разложения
можно представить в виде суммы конечного числа простейших рациональных дробей первого – четвертого типов. Для разложения ![]() на простейшие дроби необходимо разложить знаменатель Qm(x) на линейные и квадратные множители, для чего надо решить уравнение:
на простейшие дроби необходимо разложить знаменатель Qm(x) на линейные и квадратные множители, для чего надо решить уравнение:
![]() - (5)
- (5)
Теорема. Правильную рациональную дробь ![]() , где
, где ![]() , можно единственным образом разложить на сумму простейших дробей:
, можно единственным образом разложить на сумму простейших дробей:
![]()
![]() - (6)
- (6)
(A1, A2, …, Ak, B1, B2, …, B1, M1, N1, M2, M2, …, Ms, Ns – некоторые действительные числа).
Метод неопределенных коэффициентов. Суть метода неопределенных коэффициентов состоит в следующем. Пусть дано разложение правильной рациональной дроби ![]() по формуле (6) на простейшие дроби с неопределенными коэффициентами. Приведем простейшие дроби к общему знаменателю Qm(x) и приравняем многочлен, получившийся в числителе, многочлену Pn(x).
по формуле (6) на простейшие дроби с неопределенными коэффициентами. Приведем простейшие дроби к общему знаменателю Qm(x) и приравняем многочлен, получившийся в числителе, многочлену Pn(x).
Метод частных значений. При нахождении неопределенных коэффициентов вместо того, чтобы сравнивать коэффициенты при одинаковых степенях х, можно дать переменной х несколько частных значений (по числу неопределенных коэффициентов) и получить таким образом систему уравнений относительно неопределенных коэффициентов. Особенно выгодно применять этот метод в случае, корни знаменателя рациональной дроби ![]() просты и действительны. Тогда оказывается удобным последовательно полагать равным каждому из корней знаменателя.
просты и действительны. Тогда оказывается удобным последовательно полагать равным каждому из корней знаменателя.
Правило интегрирования рациональных дробей. Для того чтобы проинтегрировать рациональную дробь, необходимо выполнить следующие действия:
1) если рассматриваемая рациональная дробь ![]() - неправильная (k≥m), представить ее в виде суммы многочлена и правильной рациональной дроби:
- неправильная (k≥m), представить ее в виде суммы многочлена и правильной рациональной дроби:
![]()
где n < m; R(x) – многочлен;
2) если рассматриваемая рациональная дробь ![]() - правильная (n < m), представить ее в виде суммы простейших рациональных дробей по формуле (6);
- правильная (n < m), представить ее в виде суммы простейших рациональных дробей по формуле (6);
3) интеграл от рациональной дроби представить в виде суммы интегралов от целой части и от соответствующих простейших дробей и вычислить эти интегралы.
Интегрирование выражений, содержащие тригонометрические функции.
Интегралы вида ![]() Универсальная подстановка. Будем рассматривать интегралы вида:
Универсальная подстановка. Будем рассматривать интегралы вида:
![]() - (7)
- (7)
при условии, что они не являются табличными. Вычислить их можно различными методами, изложенными ранее. Иногда бывает достаточно преобразовать подынтегральное выражение, использовав тригонометрические формулы, применить методы «подведения» множителя под знак дифференциала, замены переменной или интегрирования по частям.
Для вычисления интеграла вида (7) существует общая универсальная схема вычисления, основанная на универсальной тригонометрической подстановке ![]() .
.
Интегралы вида ![]()
![]() (m, n є Z, m ≥ 0, n ≥ 0). Если хотя бы одно из чисел m и n – нечетное, то, отделяя от нечетной степени один сомножитель и выражая с помощью формулы sin2x+cos2x=1 оставшуюся четную степень через конфункцию, приходим к табличному интегралу.
(m, n є Z, m ≥ 0, n ≥ 0). Если хотя бы одно из чисел m и n – нечетное, то, отделяя от нечетной степени один сомножитель и выражая с помощью формулы sin2x+cos2x=1 оставшуюся четную степень через конфункцию, приходим к табличному интегралу.
Интегралы вида ![]() ,
, ![]() , (n є N, n > 1). Эти интегралы вычисляются подстановками tgx= t и ctgx=t соответсвенно.
, (n є N, n > 1). Эти интегралы вычисляются подстановками tgx= t и ctgx=t соответсвенно.
Если t=tgx, то x=arctgt, ![]() . Тогда:
. Тогда:
![]() .
.
Последний интеграл при n ≥ 2 является интегралом от неправильной рациональной дроби, которая вычисляется по правилу интегрирования рациональных дробей.
Аналогично если t=ctgx, то x=arcctgt, ![]() , откуда:
, откуда:
![]()
Интегралы вида ![]()
![]()
![]() (m, n є R). Они вычисляются путем разложения подынтегральной функции на слагаемые по формулам:
(m, n є R). Они вычисляются путем разложения подынтегральной функции на слагаемые по формулам:
![]()
![]()
![]()
8.Интегрирование иррациональных выражений.
Интегралы вида ![]() (m1, n1, m2, n2, … - целые числа). В этих интегралах подынтегральная функция рациональна относительно переменной интегрирования и радикалов от х. Они вычисляются подстановкой x=ts, где s – общий знаменатель дробей
(m1, n1, m2, n2, … - целые числа). В этих интегралах подынтегральная функция рациональна относительно переменной интегрирования и радикалов от х. Они вычисляются подстановкой x=ts, где s – общий знаменатель дробей ![]() ,
, ![]() , … При такой замене переменной все отношения
, … При такой замене переменной все отношения ![]() = r1,
= r1, ![]() = r2, … являются целыми числами, т. е. интеграл приводится к рациональной функции от переменной t:
= r2, … являются целыми числами, т. е. интеграл приводится к рациональной функции от переменной t:
![]()
![]()
Интегралы вида 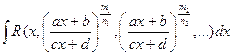 (m1, n1, m2, n2, … - целые числа). Эти
интегралы подстановкой:
(m1, n1, m2, n2, … - целые числа). Эти
интегралы подстановкой:
![]()
где s – общий знаменатель дробей ![]() ,
, ![]() , …, сводятся к рациональной функции от переменной t.
, …, сводятся к рациональной функции от переменной t.
Интегралы вида ![]()
![]()
![]() Для вычисления интеграла I1 выделяется полный квадрат под знаком радикала:
Для вычисления интеграла I1 выделяется полный квадрат под знаком радикала:
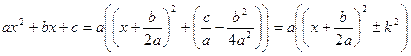
и применяется подстановка:
![]() , dx=du.
, dx=du.
В результате этот интеграл сводится к табличному: ![]()
В числителе интеграла I2 выделяется дифференциал выражения, стоящего под знаком радикала, и этот интеграл представляется в виде суммы двух интегралов:
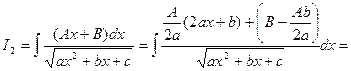
![]()
![]()
![]()
![]()
где I1 – вычисленный выше интеграл.
Вычисление интеграла I3 сводится к вычислению интеграла I1 подстановкой:
![]()
![]()
Интеграл вида ![]() Частные случаи вычисления интегралов данного вида рассмотрены в предыдущем пункте. Существует несколько различных приемов их вычисления. Рассмотрим один из таких приемов, основанный на применении тригонометрических подстановок.
Частные случаи вычисления интегралов данного вида рассмотрены в предыдущем пункте. Существует несколько различных приемов их вычисления. Рассмотрим один из таких приемов, основанный на применении тригонометрических подстановок.
Квадратный трехчлен ax2+bx+c путем выделения полного квадрата и замены переменной может быть представлен в виде ![]() Таким образом, достаточно ограничиться рассмотрением трех видов интегралов:
Таким образом, достаточно ограничиться рассмотрением трех видов интегралов:
![]()
![]()
![]()
Интеграл ![]() подстановкой
подстановкой
u=ksint (или u=kcost)
сводится к интегралу от рациональной функции относительно sint и cost.
Интегралы вида ![]() (m, n, p є Q, a, b є R). Рассматриваемые интегралы, называемые интегралами от дифференциального бинома
(m, n, p є Q, a, b є R). Рассматриваемые интегралы, называемые интегралами от дифференциального бинома ![]() , выражаются через элементарные функции только в следующих трех случаях:
, выражаются через элементарные функции только в следующих трех случаях:
1) если p є Z, то применяется подстановка:
x=ts,
где s – общий знаменатель дробей m и n;
2) если ![]() Z, то используется подстановка:
Z, то используется подстановка:
a+bxn=ts,
где s – знаменатель дроби ![]()
3) если ![]() Z, то применяется подстановка:
Z, то применяется подстановка:
ax-n+b=ts,
где s – знаменатель дроби ![]()
Похожие работы
... они не требуют от учащихся дополнительных знаний по физике, а, следовательно, удовлетворяют как принципу научности, так и принципу доступности материала. 2.2. Изучение свойств определенного интеграла с помощью физических моделей При изучении интеграла существенным является отбор свойств, которые необходимо знать ученикам. Их должно быть достаточно для рассмотрения приложений интеграла и в ...
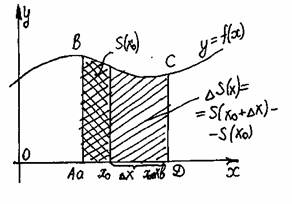
... между этими графиками равна b ò ((f(x)–g(x))dx a Функции f(x) и g(x) произвольные и неотрицательные b b b S=ò f(x)dx – ò g(x)dx = ò (f(x)–g(x))dx a a a b b S=ò f(x)dx + ò g(x)dx a a Применение интеграла I. В физике. Работа силы (A=FScosa, cosa ¹ 1) Если на частицу действует сила F, кинетическая ...
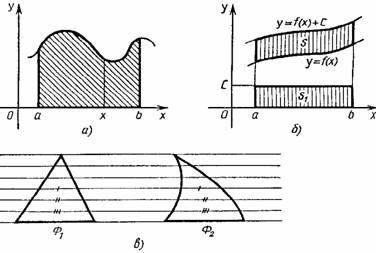
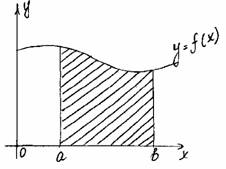
... выражением, – переменной интегрирования; отрезок называется промежутком интегрирования. Теорема 1. Если функция непрерывна на отрезке , то она интегрируема на этом отрезке. 2. Геометрический смысл определенного интеграла Пусть на отрезке задана непрерывная неотрицательная функция . Криволинейной трапецией называется фигура, ограниченная сверху графиком функции y = f(x), снизу – осью ...
... элементарной функцией, то первообразная от элементарной функции может оказаться и не представимой с помощью конечного числа элементарных функций. Из определения 2 следует: 1.Производная от неопределенного интеграла равна подынтегральной функции, т.е.если F′ (x)= f(x), то и (∫ f(x)dx)′= (F(x)+C)′=f(x). (4) Последнее равенство нужно понимать в том смысле, что ...
0 комментариев