Навигация
11. Теорема о среднем.
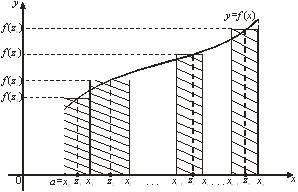
Если функция f(x) непрерывна на отрезке [a; b], то существует такая точка ![]() [a; b], что
[a; b], что
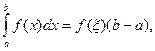
т. е. определенный интеграл от переменной функции равен произведению значения подынтегральной функции в некоторой промежуточной точке ξ отрезка интегрирования [a; b] и длины b-a этого отрезка.
12. Производная определенного интеграла по верхнему пределу. Формула Ньютона-Лейбница.
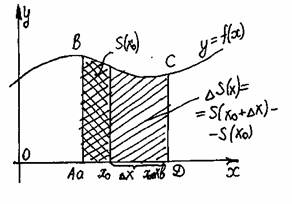
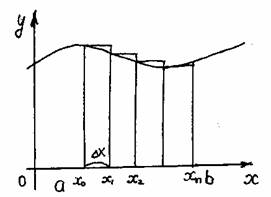
До сих пор мы рассматривали определенный интеграл с постоянными пределами интегрирования a и b. Если оставить постоянным нижний предел интегрирования a, а верхний х изменять так, чтобы x є [a; b], то величина интеграла будет изменяться. Интеграл вида:
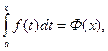 x є [a; b],
x є [a; b],
называется определенным интегралом с переменным верхним пределом и является функцией верхнего предела х. Здесь для удобства переменная интегрирования обозначена буквой t, а верхний предел интегрирования – буквой х.
Теорема. Производная определенного интеграла от непрерывной функции f(x) по его переменному верхнему пределу существует и равна подынтегральной функции, в которой вместо переменной интегрирования подставлено значение верхнего предела:
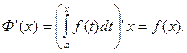
Формула Ньютона-Лейбница. Формула Ньютона-Лейбница дает правило вычисления определенного интеграла: значение определенного интеграла на отрезке [a; b] от непрерывной функции f(x) равно разности значений любой ее первообразной, вычисленной при x=b и x=a.
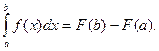 - (9)
- (9)
13. Замена переменной и интегрирования по частям в определенном интеграле.
Замена переменной в определенном интеграле. Этот метод, как и в случае неопределенного интеграла, позволяет упростить вычисления, т. е. привести подынтегральное выражение к соответствующей табличной форме. Применение замены переменной в определенном интеграле базируется на следующей теореме.
Теорема. Если функция f(x) непрерывная на отрезке [a; b], а функция x=φ(t) непрерывно дифференцируема на отрезке [t1; t2], причем φ([t1; t2])=[a; b] и φ(t1)=a, φ(t2)=b, то справедлива формула:
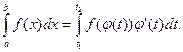 - (10)
- (10)
Интегрирование по частям в определенном интеграле. Пусть u(x) и v(x) – дифференцируемые на отрезке [a; b] функции переменной х. Тогда d(uv)=udv+vdu. Проинтегрируем обе части последнего равенства на отрезке [a; b]:
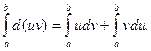 - (11)
- (11)
С другой стороны, по формуле Ньютона-Лейбница
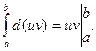
Следовательно, формула (11) принимает вид:
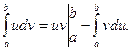 - (12)
- (12)
Формула (12) называется формулой интегрирования по частям в определенном интеграле.
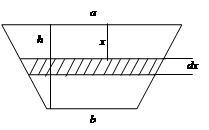
15. Вычисление площадей плоских фигур.
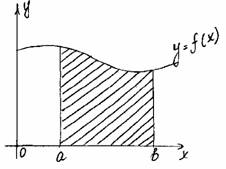
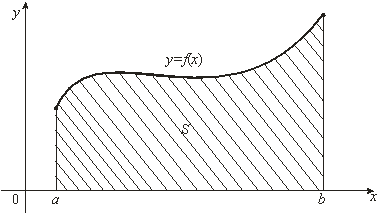
Площадь криволинейной трапеции, ограниченной кривой y=f(x) [f(x) ≥ 0], прямыми x=a и x=b и отрезками [a; b] оси Ох, вычисляется по формуле:
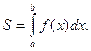
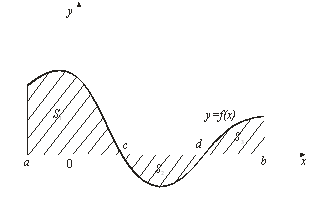
Площадь фигуры, ограниченной кривыми y=f1(x) и y=f2(x)[f1(x) ≤ f2(x)] и прямыми x=a и x=b, находится по формуле:
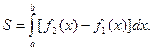
Если кривая задана параметрическими уравнениями x=x(t), y=y(t), то площадь криволинейной трапеции, ограниченной этой кривой, прямыми x=a, x=b и отрезком [a; b] оси Ох, выражается формулой:
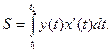
где t1 и t2 определяются из уравнений a=x(t1), b=x(t2) [y(t) ≥ 0 при t1 ≤ t ≤ t2].
Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением ρ=ρ(θ) и двумя полярными радиусами θ=α, θ=β (α < β), выражается интегралом:
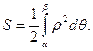
16. Определение и вычисление длины кривой, дифференциал кривой.
Если кривая y=f(x) на отрезке [a; b] - гладкая (т. е. производная y’=f’(x) непрерывна), то длина соответствующей дуги этой кривой находится по формуле:
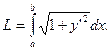
При параметрическом задании кривой x=x(t), y=y(t) [x(t) и y(t) – непрерывно дифференцируемые функции] длина дуги кривой, соответствующая монотонному изменению параметра t от t1 до t2, вычисляется по формуле:
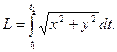
Если гладкая кривая задана в полярных системах координатах уравнением ρ=ρ(θ), α ≤ θ ≤ β, то длина дуги равна:
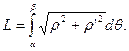
Дифференциал длины дуги. Длина дуги кривой определяется формулой:
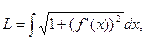
где y=f(x) ![]() [a; b]. Предположим, что в этой формуле нижний передел интегрирования остается постоянным, а верхний изменяется. Обозначим верхний предел буквой х, а переменную интегрирования буквой t. Длина дуги будет функцией верхнего предела:
[a; b]. Предположим, что в этой формуле нижний передел интегрирования остается постоянным, а верхний изменяется. Обозначим верхний предел буквой х, а переменную интегрирования буквой t. Длина дуги будет функцией верхнего предела:
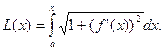
Практические задания
1. Найти неопределенный интеграл, результат проверить дифференцированием:
1) ![]() .
.
Решение:
![]()
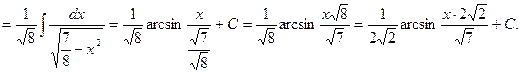
Проверка:
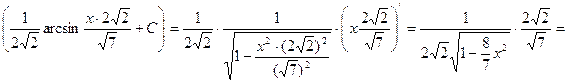
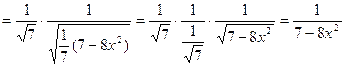 - верно.
- верно.
___________________________________________________________________________
2) ![]() .
.
Решение:
![]()
![]()
Проверка:
![]() - верно.
- верно.
__________________________________________________________________________________
3) ![]() .
.
Решение:
![]()
![]()
![]()
![]()
Проверка:
![]() - верно.
- верно.
___________________________________________________________________________
4) ![]() .
.
Решение:
![]()
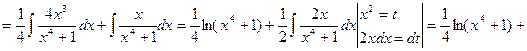
![]()
Проверка:
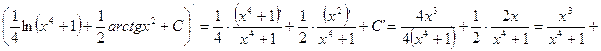
![]() - верно.
- верно.
___________________________________________________________________________
5) ![]() .
.
Решение:
![]()
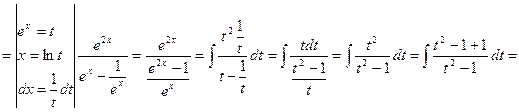
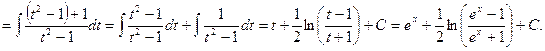
Проверка:
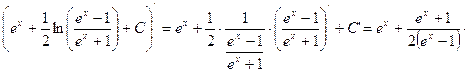
![]()
![]()
![]() - верно.
- верно.
___________________________________________________________________________
6) ![]() .
.
Решение:
![]()
![]()
Проверка:
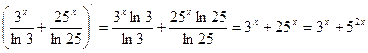 - верно.
- верно.
___________________________________________________________________________
7) ![]() .
.
Решение:
![]()
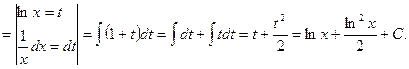
Проверка:
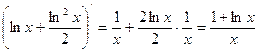 - верно.
- верно.
___________________________________________________________________________
8) ![]()
Решение:
![]()
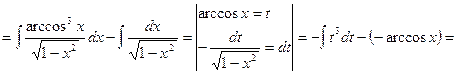
![]()
Проверка:
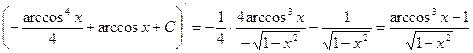 - верно.
- верно.
__________________________________________________________________________________
9) ![]() .
.
Решение:
![]()
![]()
Проверка:
![]() - верно.
- верно.
___________________________________________________________________________
2. Найти неопределенные интегралы:
1) ![]() .
.
Решение:
![]()
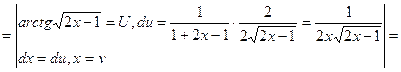
![]()
![]()
___________________________________________________________________________
2) ![]() .
.
Решение:
![]()
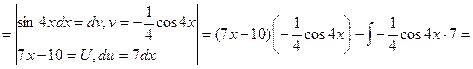
![]()
___________________________________________________________________________
3) ![]() .
.
Решение:
![]()
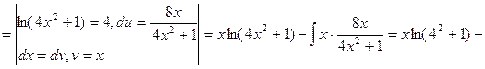
![]()
___________________________________________________________________________
4) ![]() .
.
Решение:
![]()
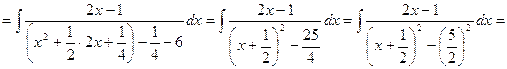
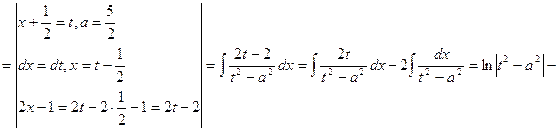
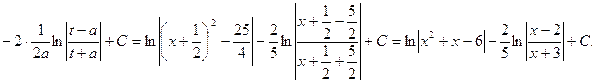
___________________________________________________________________________
5) ![]() .
.
Решение:
![]()
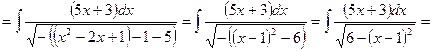
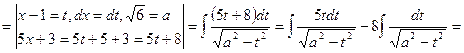
![]()
![]()
___________________________________________________________________________
6) ![]() .
.
Решение:
![]()
![]()
![]()
___________________________________________________________________________
7) ![]() .
.
Решение:
![]()
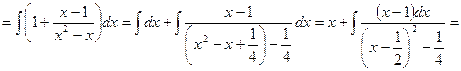
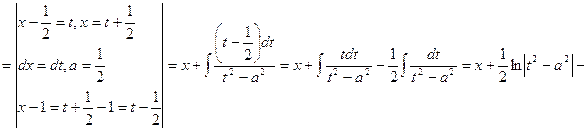
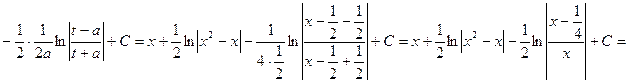
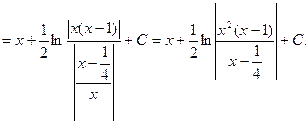
___________________________________________________________________________
8) ![]() .
.
Решение:
![]()
![]()
![]()
![]()
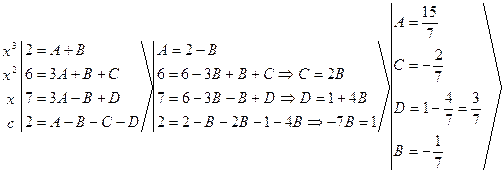
![]()
![]()
![]()
___________________________________________________________________________
9) ![]() .
.
Решение:
![]()
![]()
___________________________________________________________________________
10) ![]() .
.
Решение:
![]()
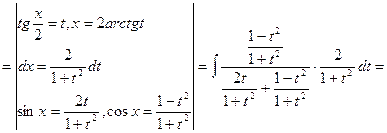
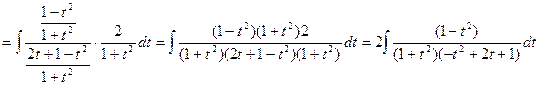
![]()
![]()
![]()
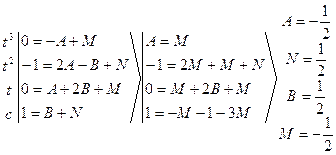
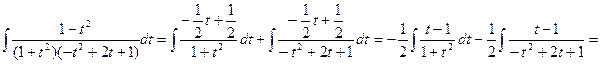
![]()
![]()
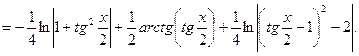
__________________________________________________________________________________
11) ![]() .
.
Решение:
![]()
___________________________________________________________________________
12) 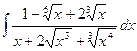 .
.
Решение:
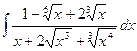
___________________________________________________________________________
13) ![]() .
.
Решение:
![]()
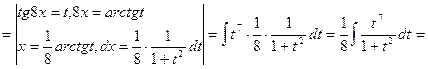
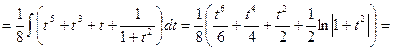
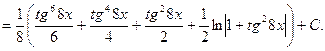
___________________________________________________________________________
14) 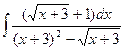 .
.
Решение:
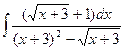
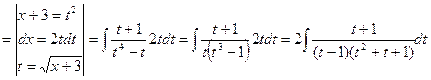
![]()
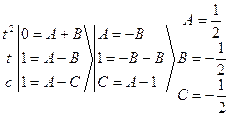
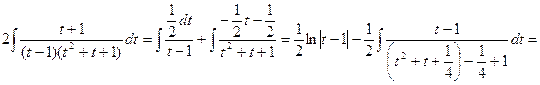
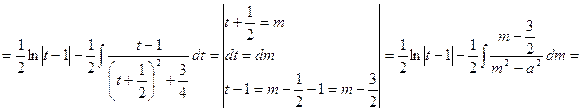
![]()
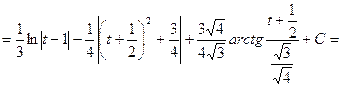
![]()
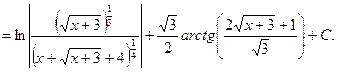
___________________________________________________________________________
15) ![]() .
.
Решение:
![]()
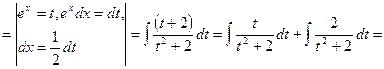
![]()
![]()
___________________________________________________________________________
3. Вычислить определенный интеграл:
1) 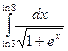 .
.
Решение:
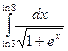
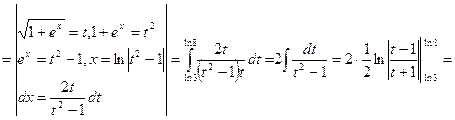
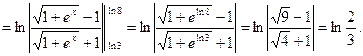
___________________________________________________________________________
2) ![]() .
.
Решение:
![]()
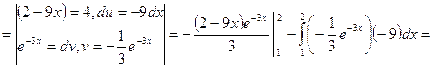
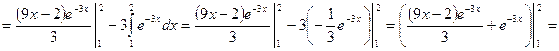
![]()
___________________________________________________________________________
3) 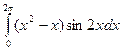 .
.
Решение:
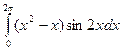
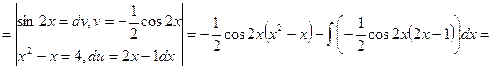
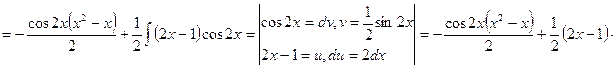
![]()
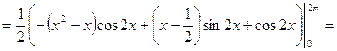
![]()
____________________________________________________________________________
4. Найти несобственные интегралы или доказать их расходимость:
1) ![]() .
.
Решение:
![]() - интеграл I рода.
- интеграл I рода.
![]()
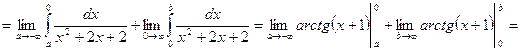
![]()
![]() - сходящийся.
- сходящийся.
____________________________________________________________________________
2) 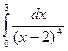 .
.
Решение:
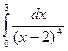 - интеграл II рода.
- интеграл II рода.
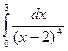
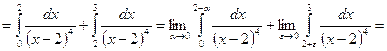
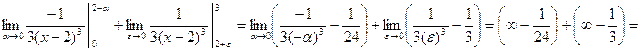
![]() - расходящийся.
- расходящийся.
____________________________________________________________________________
3) 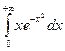 .
.
Решение:
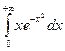
___________________________________________________________________________________
![]()
Похожие работы
... они не требуют от учащихся дополнительных знаний по физике, а, следовательно, удовлетворяют как принципу научности, так и принципу доступности материала. 2.2. Изучение свойств определенного интеграла с помощью физических моделей При изучении интеграла существенным является отбор свойств, которые необходимо знать ученикам. Их должно быть достаточно для рассмотрения приложений интеграла и в ...
... между этими графиками равна b ò ((f(x)–g(x))dx a Функции f(x) и g(x) произвольные и неотрицательные b b b S=ò f(x)dx – ò g(x)dx = ò (f(x)–g(x))dx a a a b b S=ò f(x)dx + ò g(x)dx a a Применение интеграла I. В физике. Работа силы (A=FScosa, cosa ¹ 1) Если на частицу действует сила F, кинетическая ...
... выражением, – переменной интегрирования; отрезок называется промежутком интегрирования. Теорема 1. Если функция непрерывна на отрезке , то она интегрируема на этом отрезке. 2. Геометрический смысл определенного интеграла Пусть на отрезке задана непрерывная неотрицательная функция . Криволинейной трапецией называется фигура, ограниченная сверху графиком функции y = f(x), снизу – осью ...
... элементарной функцией, то первообразная от элементарной функции может оказаться и не представимой с помощью конечного числа элементарных функций. Из определения 2 следует: 1.Производная от неопределенного интеграла равна подынтегральной функции, т.е.если F′ (x)= f(x), то и (∫ f(x)dx)′= (F(x)+C)′=f(x). (4) Последнее равенство нужно понимать в том смысле, что ...
0 комментариев