Навигация
Конспект лекций по дискретной математике
Приложение Булевой алгебры к синтезу комбинационных схем
Двоичная система логики:
1. Элементы Булевой алгебры:
а) числа
b) переменные
с) операции
d) выражения
e) функции
f) законы
А) Числа:
Два числа: логический ноль и логическая единица в Булевой алгебре отождествляются с понятиями “истина” и ”ложь”.
В) Переменные:
Булевы (логические, двоичные) переменные называются переменными, принимающими значение из множества - ноль и единица.
С) Операции:
1. Отрицание (инверсия).
2. Конъюнкция (логическое умножение).
3. Дизъюнкция (логическое сложение).
Унарной является операция отрицания.
Обозначения:
1.
Отрицание ![]() ,
щ
x
,
щ
x
2. Конъюнкция a&b, a·b, ab, aЩb
3. Дизъюнкция aЪb
D) Выражения:
Переменные, знакооперации, соединенные вместе при возможном наличии скобок для задания порядка выполнения операций.
Приоритет задается порядком операции.
Е) Функции:
Булевой (логической) функцией называется такая функция, аргументами которой являются булевы переменные, и сама функция принимает значение из множества ноль и единица.
Областью определения Булевой функции является совокупность 2n двоичных наборов ее аргументов. Набор аргументов можно рассматривать как n-компонентный двоичный вектор.
Формы задания Булевой функции:
1. Аналитическая (в виде логического выражения)
2. Табличная (в виде таблицы истинности)
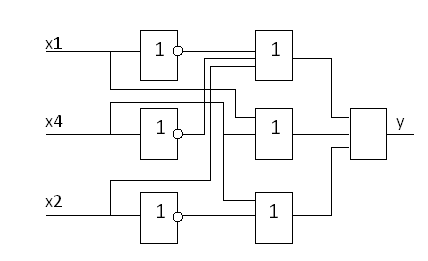
3. Графическая
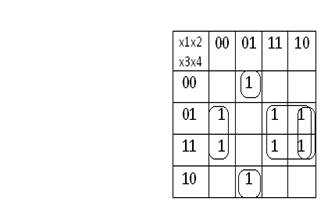
4. Таблично-графическая (в виде карты Карно)
5. Числовая
6. Символическая форма
1) Аналитическая:
_ _
y=(x1 Ъ x2) x3
_ _ _ _ _ _
y=x1 x2 x3 Ъ x1 x2 x3 Ъ x1 x2 x3
2) Табличная:
x1 | x2 | x3 | _ x1 Ъ x2 | y |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
Переход от аналитической к табличной однозначен! Обратный переход не является однозначным.
Основные законы (тождества)
1) ab=ba
aЪb=bЪa
2) Ассоциативный:
a(bc)=(ab)c
aЪ(bЪc)= (aЪb) Ъc
3) Дистрибутивный:
a(bЪc)=abЪac
aЪ(bc)=(aЪb)(aЪc)
4) Закон двойного отрицания:
=
a=a
5) Тавтологии:
aa=a
aЪa=a
6) Законы нулевого элемента:
a0=0
aЪ0=a
7) Законы единичного элемента:
а1=а
аЪ1=1
8) Законы дополнительного элемента:
_
В Булевой алгебре дополнительным элементом к а является а.
_ _
аЪа=1; аа=0
9) Двойственности (деМоргана):
__ _ _
ab=aЪb
___ _ _
![]()
![]()
![]()
![]()
![]()
![]() aЪb=a
b
aЪb=a
b
Cледствия: ab=aЪb; aЪb=a b
10) Поглощения:
aЪab=a
a(aЪb)=a
11) Сокращения:
_
аЪаb=aЪb
_
a(aЪb)=ab _ _ _ _
Cледствия: aЪab=aЪb; a(aЪb)=ab
12) Склеивания:
_ _
abЪab=a; (aЪb)(aЪb)=a
Комментарии:
1) Для доказательства законов можно использовать:
а) Метод совершенной индукции.
б) Использование одних законов для доказательства других законов.
Метод совершенной индукции состоит в доказательстве эквивалентности левой и правой части на всем множестве наборов аргументов. Для этого составляется таблица истинности.
2) Большинство законов задается парой соотношений, при этом одно соотношение можно получить из другого заменив операции конъюнкции на дизъюнкцию или дизъюнкцию на конъюнкцию (метод не применим в законах, в которых участвуют константы). С константами же константы заменяются на противоположные значения. (Дуальность законов Булевой алгебры)
3) Некоторые законы можно распространять на произвольное число элементов.
4) В любом законе можно заменить любую букву на произвольное логическое выражение.
5) Законы применяются для упрощения Булевых функций.
Разнообразие Булевых функций.
Похожие работы
... которой были разработаны в последней четверти 19 века Георгом Кантором. Цель контрольной работы – ознакомится с основными понятиями и методами решения по дискретной математике, уметь применить полученные знания при решении практического задания. Задание 1 Представить с помощью кругов Эйлера множественное выражение . Используя законы и свойства алгебры множеств, упростить заданное ...
в и формальных систем является центральной в дисциплине. В настоящие время от нее возникли ответвления, например, разработка алгоритмических языков программирования.Одной из важнейших проблем в дискретной математики является проблема сложности вычислений.Теория сложности вычислений помогает оценить расход времени и памяти при решении задач на ЭВМ. Теория сложности позволяет выделить объективно ...
глядит следующим образом: ( ( A – F) ( B A ) ) Ç ( E A ÇB ) ) Минимизация проводится с использованием восемнадцати законов. (см. литературы 2) 1) (( A – F) ( B A )) = (( A F) &# ...
... чисел . Обратным ему будет отображение . Для таких отображений справедливо следующее тождество: 9. КОМПОЗИЦИЯ , то их композицией (произведением) называют , причем, если осуществляется композиция, то . В математике такое отображение называют сложной функцией, y – промежуточный аргумент. Для композиции справедливо следующие отображения: - коммутативное - - ассоциативное - ...
0 комментариев