Навигация
2.1 Исследование функции.
Вычислим первую и вторую производные данной функции
![]()
![]()
Необходимо выбрать интервал, на котором будем находить решение.
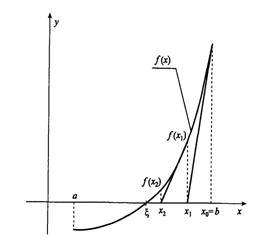
Для отделения корней существует несколько способов. Наиболее популярные из них – графический и аналитический.
В литературе рассматриваются эти способы по отдельности. По заданию курсовой работы требуется отделить корни каждым из этих способов. Рискну нарушить это требование, и объединить эти два способа в один. То есть исследовать функцию аналитически и по результатам исследования построить приблизительный график функции.
Областью значений исходного уравнения является вся ось ![]() .
.
Приравняв первую производную к нулю, мы можем получить критические точки данной функции (точки минимумов и максимумов, или же точки, в которых функция не определена).
![]()
![]()
![]()
Стоит отметить, что для вычисления квадратного корня, также применимы числовые методы, на которых и основаны микрокалькуляторы и программы для ЭВМ. Данные методы основаны на логарифмировании корня и последующего вычисления.
![]()
![]() вычисляется при помощи числового ряда
вычисляется при помощи числового ряда
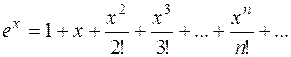
Уравнение ![]() имеет решение
имеет решение 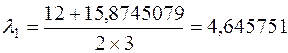 ,
, 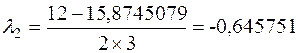 . Изменив знак равенства на знак неравенства (< или >), можем найти промежутки возрастания и убывания функции.
. Изменив знак равенства на знак неравенства (< или >), можем найти промежутки возрастания и убывания функции.
Функция возрастает на промежутке ![]() и убывает на промежутке
и убывает на промежутке ![]() . Подставив в исходное уравнение значения критических точек, имеем в результате для
. Подставив в исходное уравнение значения критических точек, имеем в результате для ![]() и для
и для ![]() .
.
Приравняв вторую производную к нулю, мы можем найти точку перегиба и, соответственно, найти интервал, на котором функция выпуклая и вогнутая.
![]()
![]()
![]()
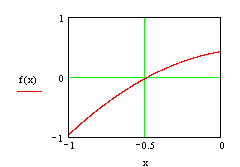
Далее необходимо найти, интервалы, в которых график функции пересекает ось ![]() .
.
Сразу можно определиться, что так при ![]() значение функции больше нуля, а при
значение функции больше нуля, а при ![]() - меньше нуля, то одна из точек пересечения, будет лежать на данном интервале. Произведя не хитрые математические вычисления значения функции для
- меньше нуля, то одна из точек пересечения, будет лежать на данном интервале. Произведя не хитрые математические вычисления значения функции для ![]() , сузим интервал до
, сузим интервал до ![]() .
.
Далее рассмотрим оставшиеся два интервала.
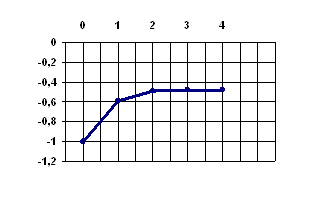
Известно, что при ![]() - значение функции отрицательно, а в первой критической точке положительно, то будем сужать этот промежуток. В данном случае применим метод половинного деления.
- значение функции отрицательно, а в первой критической точке положительно, то будем сужать этот промежуток. В данном случае применим метод половинного деления.
|
|
|
| 0 | 58 |
| -100 | -1059042 |
| -50 | -139492 |
| -25 | -19092 |
| -12 | -2426 |
| -6 | -320 |
| -3 | 4 |
| -5 | -172 |
| -4 | -66 |
|
|
|
| 4 | -10 |
| 100 | 939158 |
| 50 | 109608 |
| 25 | 11708 |
| 12 | 814 |
| 6 | 4 |
| 5 | -12 |
Таким образом получили еще один интервал ![]() .
.
Следующий будет от ![]() и до бесконечности.
и до бесконечности.
Произведем аналогичные вычисления и получим промежуток ![]()
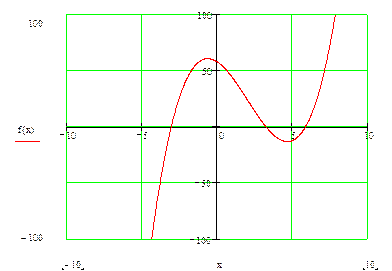
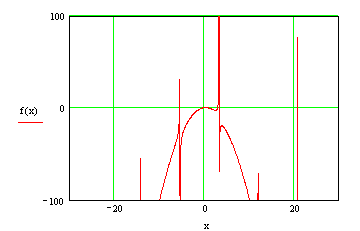
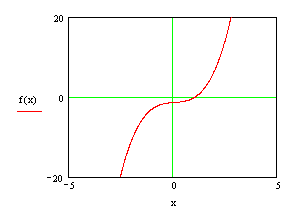
На основании произведенного анализа построим график исходной функции.
Похожие работы
... затрачивается большой объем памяти для хранения промежуточных данных (u,v,p,…). Метод Рунге скорее удобен для вычисления вручную, но менее актуален в программировании. Если говорить о нахождении более оптимального метода расчета коэффициентов Фурье на ЭВМ, то таким является вышеописанное быстрое преобразование Фурье. Он позволяет сократить количество операций до . В сравнении с вышеописанными ...
... точке приближенного решения, т. е. Последовательные приближения (4) строятся по формулам: , (9) где – начальное приближение к точному решению . 4.5 Метод Зейделя на основе линеаризованного уравнения Итерационная формула для построения приближенного решения нелинейного уравнения (2) на основе линеаризованного уравнения (7) имеет вид: 4.6 Метод наискорейшего спуска Методы ...
... 35437 x4=0.58554 5 x1=1.3179137 x2=-1.59467 x3=0.35371 x4=0.58462 6 x1=1.3181515 x2=-1.59506 x3=0.35455 x4=0.58557 5. Сравнительный анализ различных методов численного дифференцирования и интегрирования 5.1 Методы численного дифференцирования 5.1.1 Описание метода Предположим, что в окрестности точки xiфункция F (x) дифференцируема достаточное число раз. ...
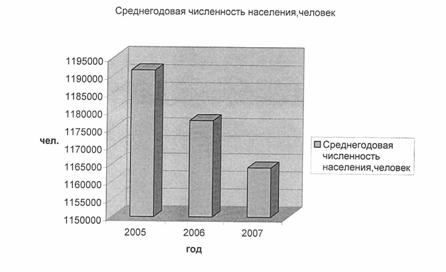
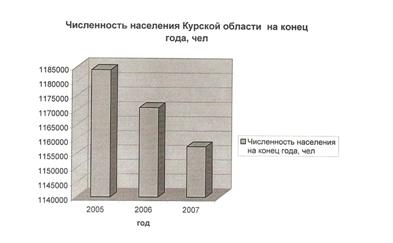
... производства, выполненных работ и услуг собственными силами по добыче полезных ископаемых в 2006 г. область занимает 22 место в России, по обрабатывающим производствам - 51, по производству и распределению электроэнергии, газа и воды - 28. 2.2 Статистическое изучение численности населения области Для характеристики численности населения представим имеющиеся данные о численности населения. ...
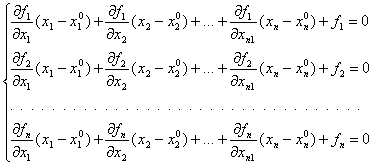
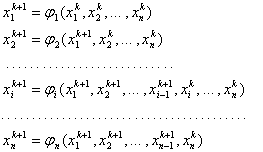
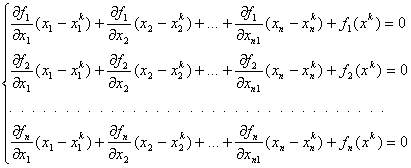

0 комментариев