Навигация
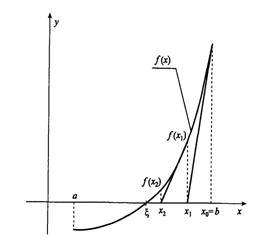
2.2 Метод хорд.
Сразу необходимо заметить, что существуют два случая (варианта) при решении методом хорд.
Случай первый. Первая и вторая производные функции имеют одинаковые знаки, т.е. ![]() .
.
В этом случае итерационный процесс осуществляем по формуле
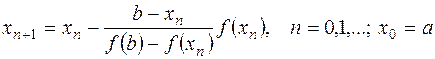
Случай второй. Первая и вторая производные функции имеют разные знаки, т.е. ![]() .
.
В этом случае итерационный процесс осуществляем по формуле
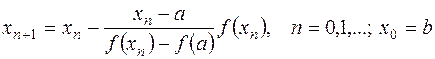
Для оценки точности приближение можно воспользоваться формулой
![]() ,
,
где ![]() при
при ![]() ,
, ![]() – точное значение корня.
– точное значение корня.
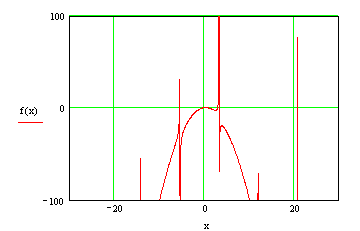
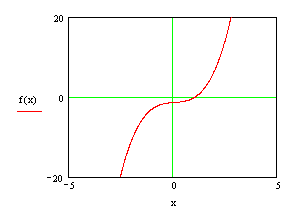
Итак решим наше уравнение ![]() методом хорд с точностью
методом хорд с точностью ![]() .
.
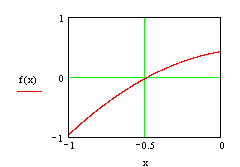
2.2.1 Интервал ![]() .
.
![]()
![]()
![]()
![]()
![]()
Так как первая и вторые производные в точке, от которой мы начинаем работать имеют различные знаки, то работаем по второму варианту.
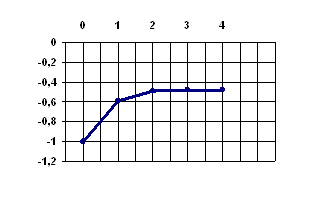
Результаты вычисления приведены в таблице.
|
|
|
|
|
|
| -4,0000000 | -3,0000000 | -66,0000000 | 4,0000000 | 0,0740741 |
| -4,0000000 | -3,1142857 | -66,0000000 | -2,3688397 | 0,0438674 |
| -4,0000000 | -3,0440850 | -66,0000000 | 1,5901736 | 0,0294477 |
| -4,0000000 | -3,0901012 | -66,0000000 | -0,9879693 | 0,0182957 |
| -4,0000000 | -3,0610770 | -66,0000000 | 0,6456578 | 0,0119566 |
| -4,0000000 | -3,0798611 | -66,0000000 | -0,4086778 | 0,0075681 |
| -4,0000000 | -3,0678974 | -66,0000000 | 0,2640772 | 0,0048903 |
| -4,0000000 | -3,0755972 | -66,0000000 | -0,1684077 | 0,0031187 |
| -4,0000000 | -3,0706743 | -66,0000000 | 0,1083107 | 0,0020058 |
| -4,0000000 | -3,0738353 | -66,0000000 | -0,0692833 | 0,0012830 |
| -4,0000000 | -3,0718112 | -66,0000000 | 0,0444729 | 0,0008236 |
| -4,0000000 | -3,0731096 | -66,0000000 | -0,0284836 | 0,0005275 |
| -4,0000000 | -3,0722776 | -66,0000000 | 0,0182690 | 0,0003383 |
| -4,0000000 | -3,0728111 | -66,0000000 | -0,0117068 | 0,0002168 |
| -4,0000000 | -3,0724692 | -66,0000000 | 0,0075061 | 0,0001390 |
| -4,0000000 | -3,0726884 | -66,0000000 | -0,0048109 | 0,0000891 |
| -4,0000000 | -3,0725479 | -66,0000000 | 0,0030843 | 0,0000571 |
| -4,0000000 | -3,0726380 | -66,0000000 | -0,0019770 | 0,0000366 |
![]()
2.2.2 Интервал ![]() .
.
![]()
![]()
![]()
![]()
![]()
Так как первая и вторые производные в точке, от которой мы начинаем работать имеют различные знаки, то работаем по второму варианту.
Результаты вычисления приведены в таблице.
|
|
|
|
|
|
| 3,0000000 | 4,0000000 | 4,0000000 | -10,0000000 | -0,2222222 |
| 3,0000000 | 3,2857143 | 4,0000000 | -0,8746356 | -0,0485909 |
| 3,0000000 | 3,2344498 | 4,0000000 | -0,0423087 | -0,0023505 |
| 3,0000000 | 3,2319959 | 4,0000000 | -0,0019734 | -0,0001096 |
| 3,0000000 | 3,2318815 | 4,0000000 | -0,0000919 | -0,0000051 |
![]()
2.2.3 Интервал ![]() .
.
![]()
![]()
![]()
![]()
![]()
Так как первая и вторые производные в точке, от которой мы начинаем работать имеют одинаковые знаки, то работаем по первому варианту.
Результаты вычисления приведены в таблице.
|
|
|
|
|
|
| 5,0000000 | 6,0000000 | -12,0000000 | 4,0000000 | 0,6666667 |
| 5,7500000 | 6,0000000 | -2,0156250 | 4,0000000 | 0,3359375 |
| 5,8337662 | 6,0000000 | -0,1613014 | 4,0000000 | 0,0268836 |
| 5,8402098 | 6,0000000 | -0,0120198 | 4,0000000 | 0,0020033 |
| 5,8406885 | 6,0000000 | -0,0008909 | 4,0000000 | 0,0001485 |
| 5,8407240 | 6,0000000 | -0,0000660 | 4,0000000 | 0,0000110 |
![]()
Итак, корнями уравнения ![]() будут
будут ![]() ,
, ![]() ,
, ![]() .
.
Похожие работы
... затрачивается большой объем памяти для хранения промежуточных данных (u,v,p,…). Метод Рунге скорее удобен для вычисления вручную, но менее актуален в программировании. Если говорить о нахождении более оптимального метода расчета коэффициентов Фурье на ЭВМ, то таким является вышеописанное быстрое преобразование Фурье. Он позволяет сократить количество операций до . В сравнении с вышеописанными ...
... точке приближенного решения, т. е. Последовательные приближения (4) строятся по формулам: , (9) где – начальное приближение к точному решению . 4.5 Метод Зейделя на основе линеаризованного уравнения Итерационная формула для построения приближенного решения нелинейного уравнения (2) на основе линеаризованного уравнения (7) имеет вид: 4.6 Метод наискорейшего спуска Методы ...
... 35437 x4=0.58554 5 x1=1.3179137 x2=-1.59467 x3=0.35371 x4=0.58462 6 x1=1.3181515 x2=-1.59506 x3=0.35455 x4=0.58557 5. Сравнительный анализ различных методов численного дифференцирования и интегрирования 5.1 Методы численного дифференцирования 5.1.1 Описание метода Предположим, что в окрестности точки xiфункция F (x) дифференцируема достаточное число раз. ...
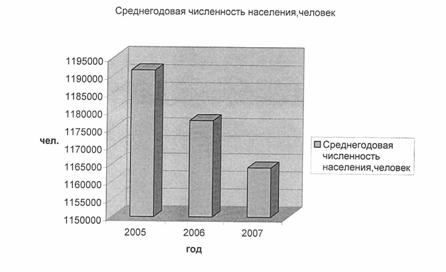
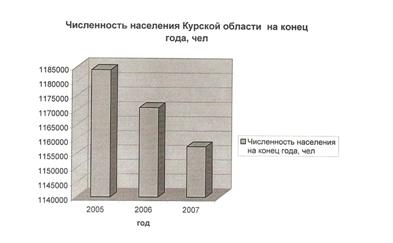
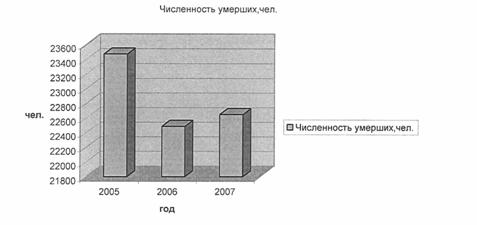
... производства, выполненных работ и услуг собственными силами по добыче полезных ископаемых в 2006 г. область занимает 22 место в России, по обрабатывающим производствам - 51, по производству и распределению электроэнергии, газа и воды - 28. 2.2 Статистическое изучение численности населения области Для характеристики численности населения представим имеющиеся данные о численности населения. ...

0 комментариев