Навигация
Используя полученные значения, определим собственные значения исходной матрицы
3. Используя полученные значения, определим собственные значения исходной матрицы.
Собственные вектора матрицы А=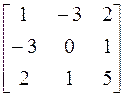 определим по формуле
определим по формуле
![]()
Для нашей матрицы, данная формула примет следующий вид
![]()
Коэффициенты ![]() определяются по схеме Горнера:
определяются по схеме Горнера:
![]()
Для ![]() имеем:
имеем:
![]()
![]()
![]()
Для ![]() имеем:
имеем:
![]()
![]()
![]()
Для ![]() имеем:
имеем:
![]()
![]()
![]()
Далее можем найти собственные векторы:
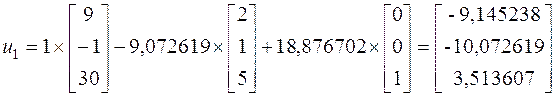
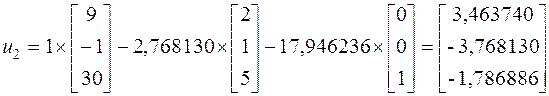
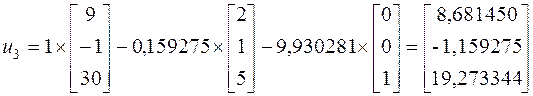
4. Для контроля полученных значений, развернем исходную матрицу А=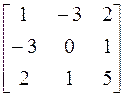 , и определим ее собственные векторы методом непосредственного развертывания.
, и определим ее собственные векторы методом непосредственного развертывания.
Характеристический многочлен для данной матрицы имеет вид:
![]() .
.
Находим ![]() .
.
Число диагональных миноров второго порядка у матрицы второго порядка 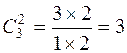 .
.
Выписываем эти миноры и складываем их:
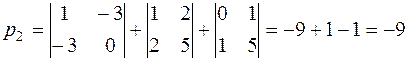 .
.
И, в заключение, находим
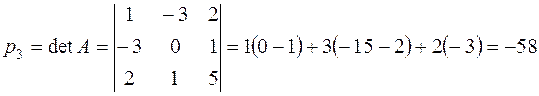
Таким образом, характеристическое уравнение имеет вид
![]()
Данное уравнение идентично уравнению, полученному при помощи метода Крылова. Нет смысла заново его решать. Воспользуемся уже вычисленными корнями (их средним значением).
Определим собственный вектор ![]() , соответствующий
, соответствующий ![]() .
.
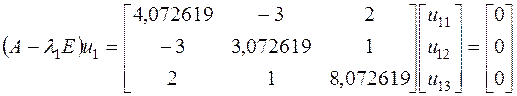 , или
, или
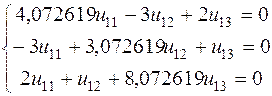
Из третьего уравнения системы выведем ![]() и подставим его в первое уравнение системы
и подставим его в первое уравнение системы
![]()
![]()
Примем ![]() , тогда
, тогда ![]() и
и ![]() .
.
Итак, искомый вектор матрицы ![]() , найденный с точностью до постоянного множителя
, найденный с точностью до постоянного множителя ![]() , для собственного значения матрицы
, для собственного значения матрицы ![]() будет:
будет:
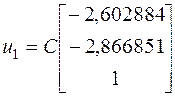
При помощи метода Крылова, мы получили точное значение собственного вектора 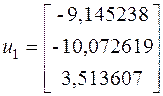 .
.
Мы можем проверить наши вычисления, взяв ![]() :
:
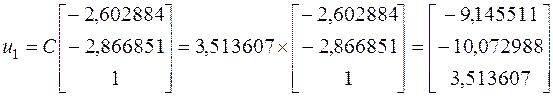
Как видно, мы получил идентичный, до третьего знака, результат.
Определим собственный вектор ![]() , соответствующий
, соответствующий ![]() .
.
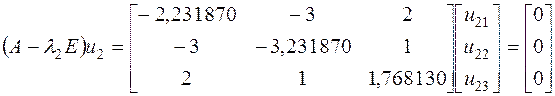 , или
, или
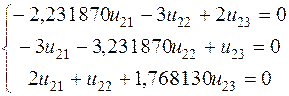
Из третьего уравнения системы выведем ![]() и подставим его в первое уравнение системы
и подставим его в первое уравнение системы
![]()
![]()
Примем ![]() , тогда
, тогда ![]() и
и ![]() .
.
Итак, искомый вектор матрицы ![]() , найденный с точностью до постоянного множителя
, найденный с точностью до постоянного множителя ![]() , для собственного значения матрицы
, для собственного значения матрицы ![]() будет:
будет:
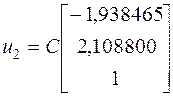
При помощи метода Крылова, мы получили точное значение собственного вектора 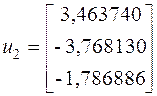 .
.
Мы можем проверить наши вычисления, взяв ![]() :
:
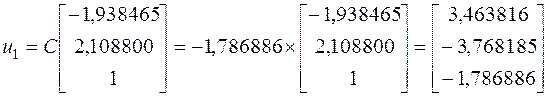
Как видно, мы получил идентичный, до третьего знака, результат.
Определим собственный вектор ![]() , соответствующий
, соответствующий ![]() .
.
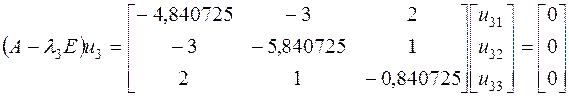 , или
, или
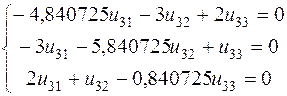
Из третьего уравнения системы выведем ![]() и подставим его в первое уравнение системы
и подставим его в первое уравнение системы
![]()
![]()
Примем ![]() , тогда
, тогда ![]() и
и ![]() .
.
Итак, искомый вектор матрицы ![]() , найденный с точностью до постоянного множителя
, найденный с точностью до постоянного множителя ![]() , для собственного значения матрицы
, для собственного значения матрицы ![]() будет:
будет:
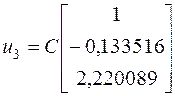
При помощи метода Крылова, мы получили точное значение собственного вектора 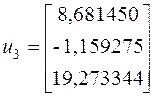 .
.
Мы можем проверить наши вычисления, взяв ![]() :
:
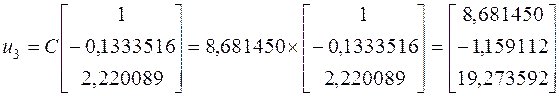
Как видно, мы получил идентичный, до третьего знака, результат.
Похожие работы
... затрачивается большой объем памяти для хранения промежуточных данных (u,v,p,…). Метод Рунге скорее удобен для вычисления вручную, но менее актуален в программировании. Если говорить о нахождении более оптимального метода расчета коэффициентов Фурье на ЭВМ, то таким является вышеописанное быстрое преобразование Фурье. Он позволяет сократить количество операций до . В сравнении с вышеописанными ...
... точке приближенного решения, т. е. Последовательные приближения (4) строятся по формулам: , (9) где – начальное приближение к точному решению . 4.5 Метод Зейделя на основе линеаризованного уравнения Итерационная формула для построения приближенного решения нелинейного уравнения (2) на основе линеаризованного уравнения (7) имеет вид: 4.6 Метод наискорейшего спуска Методы ...
... 35437 x4=0.58554 5 x1=1.3179137 x2=-1.59467 x3=0.35371 x4=0.58462 6 x1=1.3181515 x2=-1.59506 x3=0.35455 x4=0.58557 5. Сравнительный анализ различных методов численного дифференцирования и интегрирования 5.1 Методы численного дифференцирования 5.1.1 Описание метода Предположим, что в окрестности точки xiфункция F (x) дифференцируема достаточное число раз. ...
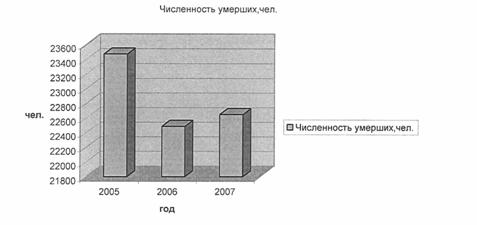
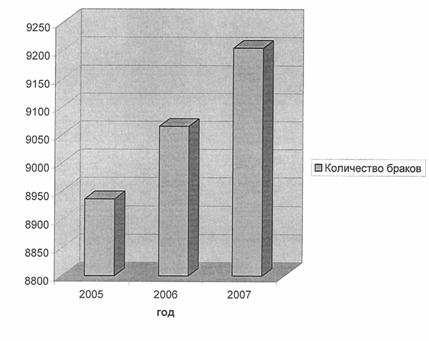
... производства, выполненных работ и услуг собственными силами по добыче полезных ископаемых в 2006 г. область занимает 22 место в России, по обрабатывающим производствам - 51, по производству и распределению электроэнергии, газа и воды - 28. 2.2 Статистическое изучение численности населения области Для характеристики численности населения представим имеющиеся данные о численности населения. ...
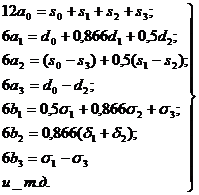
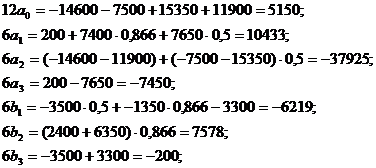
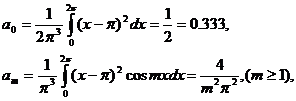
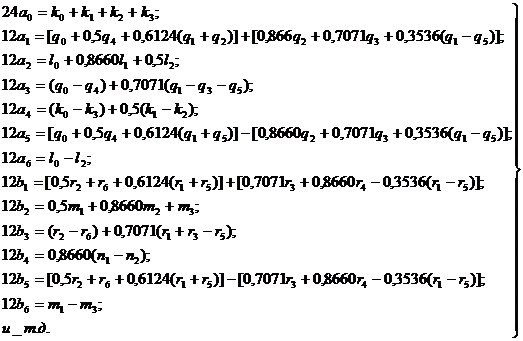
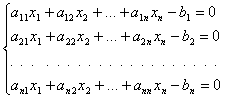
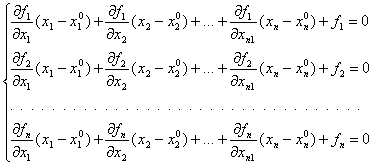
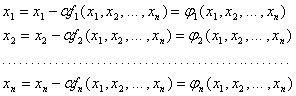
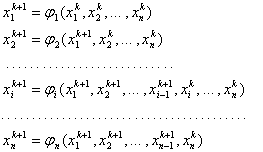
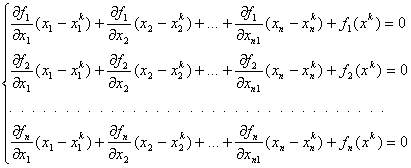

0 комментариев