Навигация
4. Выбор шага интегрирования
Для выбора шага интегрирования можно воспользоваться выражением остаточного члена. Возьмем, например, остаточный член формулы Симпсона:
.
Если ê
ê
, то ê
ê
.
По заданной точности e метода интегрирования из последнего неравенства определяем подходящий шаг.
, 
.
Однако такой способ требует оценки 
(что на практике не всегда возможно). Поэтому пользуются другими приемами определения оценки точности, которые по ходу вычислений позволяют выбрать нужный шаг h.
Разберем один из таких приемов. Пусть
,
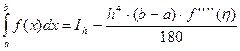где 
- приближенное значение интеграла с шагом 
. Уменьшим шаг в два раза, разбив отрезок 
на две равные части 
и 
(
).
Тогда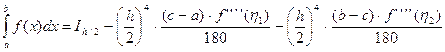 
,
Предположим теперь, что меняется не слишком быстро, так что почти постоянна: 
. Тогда 
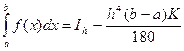и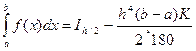 
, откуда 
, то есть 
.
Отсюда можно сделать такой вывод: если 
, то есть если 
, 
, а 
- требуемая точность, то шаг подходит для вычисления интеграла с достаточной точностью. Если же 
, то расчет повторяют с шагом 
и затем сравнивают 
и 
и т.д. Это правило называется правилом Рунге.
Однако при применении правила Рунге необходимо учитывать величину погрешности вычислений: с уменьшением абсолютная погрешность вычислений интеграла увеличивается (зависимость 
от обратно пропорциональная) и при достаточно малых может оказаться больше погрешности метода. Если превышает 
, то для данного шага применять правило Рунге нельзя и желаемая точность не может быть достигнута. В таких случаях необходимо увеличивать значение .
При выводе правила Рунге вы существенно пользовались предположением, что 
. Если имеется только таблица значений 
, то проверку «на постоянство» можно сделать непосредственно по таблице Дальнейшее развитие приведенных алгоритмов позволяет перейти к адаптивным алгоритмам, в которых за счет выбора различного шага интегрирования в разных частях отрезка интегрирования в зависимости от свойств 
уменьшается количество вычислений подынтегральной функции.
Другая схема уточнения значений интеграла - процесс Эйтнена. Производится вычисление интеграла с шагами
, причем 
. Вычисление значений 
. Тогда 
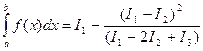(14).
За меру точности метода Симпсона принимают величину :
Похожие работы
... значение разности текущего и предыдущего значений интегрирования меньше чем 0.001, если да, то выход из цикла, если нет, то переход на блок 13. Блок 15. Вывод результатов, полученных при вычислении интеграла методом Симпсона на экран. Блок 16. Конец программы. 5. Текст программы program tr_s; uses crt,graph; var a,b:real; { Границы отрезка } r,r2:real; { Предыдущее и ...
... функции по квадратной формуле: где коэффициенты - действительные числа и узлы принадлежат k=1, 2, ... , n. Вид суммы определяет метод численного интегрирования, а разность - погрешность метода. Для метода Симпсона , (k=1, 2, ..., 2n). Правая часть формулы Симпсона является интегральной суммой и при стремится к данному интегралу. Однако при фиксированном h каждая из них ...
TITLE : Расчет интеграла методом Симпсона (парабол) * .DESCR : * : * .PARAMS : double m_Simpson (double (*func) (double, double), * : double t_fix, double t_limit, int N); * : double (*func) (double, double) - подынтегральная ф-я * : double t_fix - фиксированный первый аргумент * : double t_limit - верхний предел интегрирования, * : нижний ...
... міняють оператор інтегрування на оператор сумування. Виникаюча при такій заміні похибка називається похибкою квадратурної формули. Задача чисельного інтегрування функцій полягає в обчисленні визначеного інтеграла за значеннями інтегруємої функції в ряді точок відрізка інтегрування. Функцію заміняємо інтерполюємою функцією , а потім приблизно припускаємо [4]: (1.2) Функція повинна бути ...
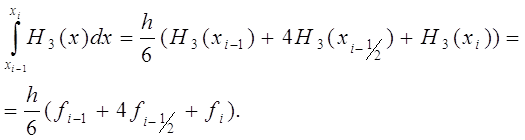
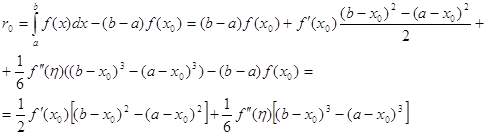
0 комментариев