Навигация
5. Примеры
Пример 1. Вычислить интеграл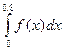 
по формуле Симпсона, если 
задана таблицей. Оценить погрешность.
Таблица 3.
|
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 |
|
| 1 | 0.995 | 0.98 | 0.955 | 0.921 | 0.878 | 0.825 | 0.765 | 0.697 |
Решение: Вычислим по формуле (1) при 
и 
интеграл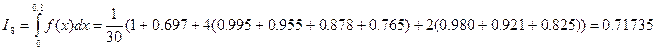 
.
.
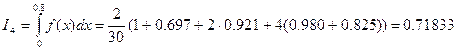По правилу Рунге получаем 
Принимаем 
.
Пример 2. Вычислить интеграл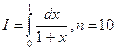 
.
Решение: Имеем 
. Отсюда h=
=0.1. Результаты вычислений приведены в таблице 4.
Таблица 4.
Вычисление интеграла по формуле Симпсона
| i |
|
|
|
| 0 | 0 | y0=1,00000 | |
| 1 | 0.1 | 0,90909 | |
| 2 | 0.2 | 0,83333 | |
| 3 | 0.3 | 0,76923 | |
| 4 | 0.4 | 0,71429 | |
| 5 | 0.5 | 0,66667 | |
| 6 | 0.6 | 0,62500 | |
| 7 | 0.7 | 0,58824 | |
| 8 | 0.8 | 0,55556 | |
| 9 | 0,9 | 0,52632 | |
| 10 | 1,0 | 0,50000=yn | |
| å | 3,45955(s1) | 2,72818(s2) |
По формуле Симпсона получим:
Подсчитаем погрешность полученного результата. Полная погрешность 
складывается из погрешностей действий 
и остаточного члена 
. Очевидно:
= 
; 
где 
- коэффициенты формулы Симпсона и e- максимальная ошибка округления значений подынтегральной функции.
= 
.
Оценим остаточный член. Так как 
, то 
. Отсюда 
max при 
и, следовательно, 
£
. Таким образом, предельная полная погрешность есть R=
и, значит,
±
.
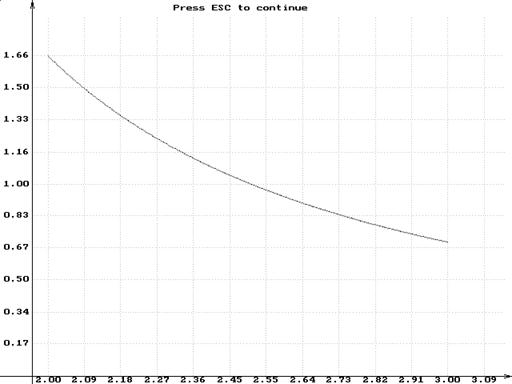
Пример3. Вычислить интеграл: 
.
Решение:
|
|
|
|
|
| 2 | -0,41613 | -0,208065 | 1 |
| 2,05 | -0,46107 | -0,224912 | |
| 2,1 | -0,59485 | -0,240405 | 4 |
| 2,15 | -0,54736 | -0,254586 | |
| 2,2 | -0,58850 | -0,267500 | 2 |
| 2,25 | -0,62817 | -0,279187 | |
| 2,3 | -0,66628 | -0,289687 | 4 |
| 2,35 | -0,70271 | -0,299026 | |
| 2,4 | -0,73739 | -0,307246 | 2 |
| 2,45 | -0,77023 | -0,314380 | |
| 2,5 | -0,80114 | -0,320465 | 4 |
| 2,55 | -0,83005 | -0,325510 | |
| 2,6 | -0,85689 | -0,329573 | 2 |
| 2,65 | -0,88158 | -0,332672 | |
| 2,7 | -0,90407 | -0,334841 | 4 |
| 2,75 | -0,92430 | -0,336109 | |
| 2,8 | -0,94222 | -0,336507 | 2 |
| ,85 | -0,95779 | -0,336067 | |
| 2,9 | -0,97096 | -0,334814 | 4 |
| 2,95 | -0,98170 | -0,332780 | |
| 3 | -0,98999 | -0,329997 | 1 |
.
Поскольку 
, 
при xÎ[2,3], для производных 
и 
получаем:
-1.4 £ £1, то есть çê£ 1,
-£ £ 3, то есть çê£ 3.
Оценки для погрешности метода Симпсона : £ 0.0000017 для 
=0.1, £ 0.0000002 для =0.05.
Чтобы погрешность округления не искажала столь точный результат для формулы Симпсона, все вычисления проводились с шестью знаками после запятой.
Окончательные результаты:
|
|
|
|
| 0,1 | -0,30335 | 0,0000017 |
| 0,05 | -0,30335 | 0,0000002 |
Похожие работы
... значение разности текущего и предыдущего значений интегрирования меньше чем 0.001, если да, то выход из цикла, если нет, то переход на блок 13. Блок 15. Вывод результатов, полученных при вычислении интеграла методом Симпсона на экран. Блок 16. Конец программы. 5. Текст программы program tr_s; uses crt,graph; var a,b:real; { Границы отрезка } r,r2:real; { Предыдущее и ...
... функции по квадратной формуле: где коэффициенты - действительные числа и узлы принадлежат k=1, 2, ... , n. Вид суммы определяет метод численного интегрирования, а разность - погрешность метода. Для метода Симпсона , (k=1, 2, ..., 2n). Правая часть формулы Симпсона является интегральной суммой и при стремится к данному интегралу. Однако при фиксированном h каждая из них ...
TITLE : Расчет интеграла методом Симпсона (парабол) * .DESCR : * : * .PARAMS : double m_Simpson (double (*func) (double, double), * : double t_fix, double t_limit, int N); * : double (*func) (double, double) - подынтегральная ф-я * : double t_fix - фиксированный первый аргумент * : double t_limit - верхний предел интегрирования, * : нижний ...
... міняють оператор інтегрування на оператор сумування. Виникаюча при такій заміні похибка називається похибкою квадратурної формули. Задача чисельного інтегрування функцій полягає в обчисленні визначеного інтеграла за значеннями інтегруємої функції в ряді точок відрізка інтегрування. Функцію заміняємо інтерполюємою функцією , а потім приблизно припускаємо [4]: (1.2) Функція повинна бути ...
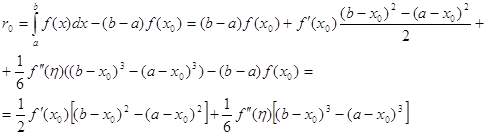
0 комментариев