Навигация
Если все элементы некоторой строки определителя состоят из
2. Если все элементы некоторой строки определителя состоят из
нулей, определитель равен нулю.
3.От перестановки двух строк определитель меняет знак.
Определитель, содержащий две одинаковые строки, равен нулю.
Общий множитель всех элементов некоторой строки определителя можно вынести за знак определителя, или, если все элементы некоторой строки определителя умножить на одно и тоже число, то определитель умножается на это число.
Определитель, содержащий две пропорциональные строки, равен нулю.
Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки, кроме i-й, те же, что и у данного определителя; i-я строка определителя состоит из первых слагаемых элементов i-й строки данного определителя, а i-я
строка другого – из вторых слагаемых элементов i-й строки.
-7-
Определитель не изменяется, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и тоже число.
1.2. Действия над матрицами.
Основные операции, которые производятся над матрицами, – сложение, вычитание, умножение, а также умножение матрицы на число. Указанные операции являются основными операциями алгебры матриц – теории, играющей весьма важную роль в различных разделах математики и естествознания.
Суммой двух матриц А и В одинаковых размеров называется матрица того же размера, элементы которой равны сумме соответствующих элементов матриц А и В. Таким образом, если
![]()
![]()
![]()
![]() а11
… а1n b11 … b1n
а11
… а1n b11 … b1n
А = ………….. ; (1) В = …………… , то (2)
am1 … аmn bm1 … bmn
![]()
![]() a11+
b11 … a1n
+ b1n
a11+
b11 … a1n
+ b1n
A + B = ………………………
am1+ bm1 … amn + bmn
Операция нахождения суммы матриц называется сложением матриц и распространяется на случай конечного числа матриц одинаковы размеров.
Так же, как и сумма, определяется разность двух матриц
![]()
![]()
a11 – b11 … a1n – b1n
![]() A
– B = ………………………
A
– B = ………………………
am1 – bm1 … amn – bmn
Операция нахождения разности двух матриц называется вычитанием матриц. Проверкой можно убедиться, что операция сложения матриц удовлетворяет следующим свойствам:
-8-
А + В = В + А; (коммутативность)
А + (В + С) = (А + В) + С; (ассоциативность)
А + О = А.
Здесь А, В, С – произвольные матрицы одинаковых размеров; О – нулевая матрица того же размера.
Произведением матрицы А = [аij] на число λ называется матрица, элементы которой получаются из соответствующих элементов матрицы А умножением их на число λ. Произведение обозначим
λА. Таким образом от умножения матрицы (1) на число, получим:
![]()
![]()
![]()
![]() a11
… a1n λa11 … λa1n
a11
… a1n λa11 … λa1n
A = ………… , то λA = ………………
am1 … amn λam1 … λamn
Операция нахождения произведения матрицы на число называется умножением матрицы на число. Матрица –А = –1А называется противоположной матрице А. Проверкой можно убедиться, что операция умножения матрицы на число удовлетворяет следующим свойствам:
1А = А;
(λ + μ)А = λА + μΑ;
λ(А + В) = λΑ+ λВ;
4) λ( μА) = (λμ)А;
5) А + (-А) = О.
Здесь А, В – произвольные матрицы; μ, λ - произвольные числа; О – нулевая матрица.
Произведение АВ матрицы А на матрицу В определяется только в том случае, когда число столбцов матрицы А равно числу строк матрицы В. Пусть матрицы А и В такие, что число столбцов матрицы А равно числу строк матрицы В:
![]()
![]()
![]()
![]()
а11 … а1n b11 … b 1n
A = …………… ; B = ………………
am1 … amn bm1 … bmn
В этом случае произведением матрицы А на матрицу В, которые
-9-
заданы в определенном порядке (А – 1ая, В – 2ая), является матрица С, элемент которой сij определяется по следующему правилу:
cij = ai1b1j + ai2b2j + … + ainbnj = ∑ n α = 1 aiαbαj,
где i = 1,2, …, m; j = 1, 2, …, k.
Для получения элемента сij матрицы произведения С = АВ нужно элементы i-й строки матрицы А умножить на соответствующие элементы j-го столбца матрицы В и полученные произведения сложить. Например, если:
![]()
![]()
![]()
![]() 1 2 3 7 8
1 2 3 7 8
![]() А
= ; В
= 9 10 , то (1)
А
= ; В
= 9 10 , то (1)
![]()
![]()
![]()
![]() 4 5 6 11 12
4 5 6 11 12
1 7 + 2 9 + 3 11 1 8 + 2 10 + 3 12 58 64
![]() АВ
= = (2)
АВ
= = (2)
4 7 + 5 9 + 6 11 4 8 + 5 10 + 6 12 139 154
Число строк матрицы С = АВ равно числу строк матрицы А, а число столбцов – числу столбцов матрицы В.
Операция нахождения произведения двух матриц называется умножением матриц. Умножение матриц некоммутативно, т.е.
АВ ≠ ВА. Убедимся в примере матриц (1). Перемножив их в обратном порядке, получим:
![]()
![]() 39 54 69
39 54 69
ВА = 49 68 87 (3)
59 82 105
Сравнив правые части выражений (2) и (3), убедимся, что АВ ≠ ВА.
Матрицы А и В, для которых АВ = ВА, называются перестановочными. Например:
![]()
![]()
![]()
![]() 1 2 -3 2
1 2 -3 2
А = ; В = перестановочны, т.к.
![]()
![]() -2 0 -2 -4
-2 0 -2 -4
![]() -7 -6
-7 -6
АВ = ВА=
-4
-10-
Проверкой можно показать, что умножение матриц удовлетворяет следующим свойствам:
А(ВС) = (АВ)С; (ассоциативность)
λ(АВ) = (λА)В = А(λВ);
А(В + С) = АВ + АС. (дистрибутивность)
Здесь А, В, С – матрицы соответствующих определению умножения матриц размеров; λ - произвольное число.
Операция умножения двух прямоугольных матриц распространяется на случай, когда число столбцов в 1ом множителе равно числу строк во 2ом, в остальных случаях произведение не определяется. А также, если матрицы А и В – квадратные одного и того же порядка, то умножение матриц всегда выполнимо при любом порядке следования сомножителей.
1.3.Обратная матрица.
Пусть дана квадратная матрица
![]()
![]() a11 … a1n
a11 … a1n
A = …………… ,
am1 … amn
![]()
![]() = A –
её определитель.
= A –
её определитель.
Если существует матрица Х такая, что АХ = ХА = Е, где Е – единичная матрица, то матрица Х называется обратной по отношению к матрице А, а сама матрица А – обратимой. Обратная матрица для А обозначается А-1.
Теорема 1.1. Для каждой обратимой матрицы существует только одна обратная ей матрица.
Д о к а з а т е л ь с т в о. Пусть для матрицы А наряду с матрицей Х существует еще хотя бы одна отличная от Х обратная матрица, которую обозначим за Х1. Тогда должны выполняться следующие условия: ХА = Е, АХ1 = Е. Умножив второе равенство на матрицу Х, получим ХАХ1 = ХЕ =Х. Но, т.к. ХА = Е, то предыдущее равенство можно записать в виде ЕХ1 = Х или Х = Х1.
Т е о р е м а д о к а з а н а.
Найдем теперь выражение для матрицы А-1 при условии, что матрица
-11-
А – обратимая. Пусть дана обратимая квадратная матрица А с элементами аij. Обозначим через Аij алгебраическое дополнение элемента аij в определителе ∆ матрицы А и составим матрицу В:
![]()
![]()
![]() А11 A21 … An1
А11 A21 … An1
B = …………………… (4)
A1n A2n … Ann
Заметим, что в i-й строке матрицы В расположены алгебраические дополнения элементов j-го столбца определителя ∆. Матрица (4) называется присоединённой для матрицы А. Докажем, что матрицы А и В удовлетворяют матричному равенству
АВ = ВА = ∆Е. (5)
Для этого вычислим элемент, стоящий в i-й строке и j-м столбце произведения АВ. Искомый элемент равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В:
ai1Aj1 + ai2Aj2 + … + ainAjn. (6)
Согласно правилу разложения определителя по элементам строки (или столбца) выражение (6) равно определителю ∆ при i = j и нулю при i ≠ j. Следовательно, мы установили, что произведение АВ есть матрица вида
![]()
![]()
![]()
![]() ∆ 0 … 0 1 0 … 0
∆ 0 … 0 1 0 … 0
Похожие работы
... , придумать “свой метод", догадаться что-то прибавить и отнять, выделить полный квадрат, на что-то разделить и умножить и т.д. Если работа в поисках более рациональный способ решения систем линейных уравнений с двумя переменными - методом подстановки будет успешна, то практическая значимость будет очевидна. Список использованной литературы 1. Алгебра 8 класс. Н.Я. Виленкин. Москва, ...
... свести к вычислению четырех определителей третьего порядка. 3-ий учебный вопрос ТЕОРЕМА КРАМЕРА Применим рассмотренную теорию определителей к решению систем линейных уравнений. 1. Система двух линейных уравнений с двумя неизвестными. (3) Здесь х1, х2 – неизвестные; а11, …, а22 – коэффициенты при неизвестных, занумерованные двумя индексами, где первый ...
... . При этом собственно нахождение обратной матрицы – процесс достаточно трудоемкий и его программирование вряд ли можно назвать элементарной задачей. Поэтому на практике чаще применяют численные методы решения систем линейных уравнений. К численным методам решения систем линейных уравнений относят такие как: метод Гаусса, метод Крамера, итеративные методы. В методе Гаусса, например, работают над ...
... 10.4 9.7 9.7 -8.4 Результат вычислений по методу Гаусса x1 = 5.0000000000E+00 x2 = -4.0000000000E+00 x3 = 3.0000000000E+00 x4 = -2.0000000000E+00 2.2 Программа решения систем линейных уравнений по методу Зейделя 2.2.1. Постановка задачи. Требуется решить систему линейных алгебраических уравнений с вещественными коэффициентами вида a11x1 + a12x2 + … + a1nxn = b1 , a21x2 + ...
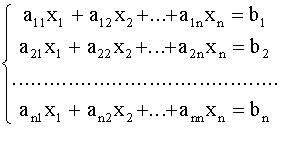
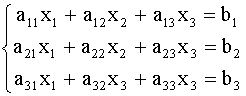



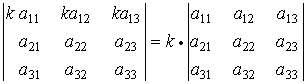
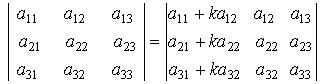


0 комментариев