Навигация
0 ∆ … 0 = ∆ 0 1 … 0
…………… ……………
0 0 … ∆ 0 0 … 1
Таким образом, АВ = ∆Е. Аналогично доказывается и равенство
ВА = ∆Е.
Пусть теперь А – невырожденная матрица (т.е. ∆ ≠ 0). Тогда, умножив обе части равенства (5) на числовой множитель 1/∆ , получим
(7)
Сравнивая равенства (5) и (7) и учитывая единственность обратной-12-
матрицы, замечаем, что
Таким образом, доказано, что, во-первых, обратимы только невырожденные матрицы, и, во-вторых, для матрицы А обратной является матрица
П![]()
![]()
![]()
![]()
![]() усть
А
невырожденная
матрица, тогда
АА-1
= Е. Переходя
в этом равенстве
к определителям,
получаем А А-1 = 1, откуда
усть
А
невырожденная
матрица, тогда
АА-1
= Е. Переходя
в этом равенстве
к определителям,
получаем А А-1 = 1, откуда
![]()
![]()
![]()
![]()
![]() А-1
= А -1.
А-1
= А -1.
Таким образом, определитель обратной матрицы равен обратной величине определителя данной матрицы. Из этого следует, что если матрица А – невырожденная, то обратная матрица А-1 также невырожденная.
Пусть теперь дана матрица А-1. Для неё обратной будет матрица
(А-1)-1.Поэтому из определения обратной матрицы будем иметь
А-1(А-1) -1 = Е. Умножив это соотношение слева на А, получим
АА-1(А-1) -1 = АЕ или (А-1) -1 = А.
-13-
Пример 1. Найти матрицу обратную матрице
![]()
![]()
1 2 3
А = –3 –1 1 .
2 1 –1
Р е ш е н и е. Проверим, обратима матрица А или нет, т.е. является ли она невырожденной:
![]()
![]()
![]()
![]() 1 2 3 1 2 5
1 2 3 1 2 5
![]()
![]() ∆А
= –3 –1 1 = –3 –1 0 = 5 –3 1 = 5 (–3 + 2) = –5 ≠ 0.
∆А
= –3 –1 1 = –3 –1 0 = 5 –3 1 = 5 (–3 + 2) = –5 ≠ 0.
2 1 –1 2 1 0 2 1
Найдем алгебраические дополнения всех элементов матрицы А:
А![]()
![]()
![]()
![]() 11
= –1 1 = 0; А12
= – –3 1 = –1;
11
= –1 1 = 0; А12
= – –3 1 = –1;
1 –1 2 –1
![]()
![]()
![]()
![]() А13
= –3 –1 = –1; А21
= – 2 3 = 5;
А13
= –3 –1 = –1; А21
= – 2 3 = 5;
2 1 1 –1
![]()
![]()
![]()
![]() А22
= 1 3 = –7; А23
= – 1 2 = 3;
А22
= 1 3 = –7; А23
= – 1 2 = 3;
2 –1 2 1
![]()
![]()
![]()
![]() А31
= 2 3 = 5; А32
= 1 3 = –10;
А31
= 2 3 = 5; А32
= 1 3 = –10;
![]() –1 1 –3 1
–1 1 –3 1
А![]() 33
= 1 2 = 5.
33
= 1 2 = 5.
–3 –1
Составим присоединённую матрицу для матрицы А:![]()
![]()
0 5 5
–1 –7 –10 .
–1 3 5
О![]()
![]() тсюда
находим обратную
матрицу:
тсюда
находим обратную
матрицу:
0 5 5
А-1 = – –1 –7 –10 .
–1 3 5
-14-
Пример 2. Найти неизвестную матрицу Х из уравнения АХ = В, если:
![]()
![]()
![]()
![]()
А = 2 3 ; В = 3 4 .
1 2 -1 1
Р е ш е н и е. Умножив обе части данного матричного уравнения слева на матрицу А-1, получим:
А-1АХ = А-1В; Х = А-1В.
Найдем А-1: ∆А = 1, А11 = 2, А12 = -1, А21 = -3, А22 = 1, следовательно,
![]()
![]()
А-1 = 2 -3 .
-1 1
Найдем матрицу Х:
![]()
![]()
![]()
![]()
![]()
![]() Х =
А-1В
= 2 -3 3 4 = 9 5 .
Х =
А-1В
= 2 -3 3 4 = 9 5 .
-1 1 -1 1 -4 -3
-15-
1.4. Ранг матрицы.
Рассмотрим произвольную прямоугольную матрицу
![]()
![]() а11 … а1n
а11 … а1n
A = …………… (8)
am1 … amn
Выделим некоторое число k строк этой матрицы и такое же число столбцов. Элементы матрицы (8), стоящие на пересечение выделенных строк и столбцов, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядка матрицы А. Если не все числа аijматрицы А равны нулю, то всегда можно указать число r такое, что у матрицы А имеется минор,
имеющий порядок r + 1 и выше, равен нулю.
Число r, представляющее собой наибольший из порядков отличных от нуля миноров матрицы А, называется рангом матрицы и обозначается rangA. Если все элементы аij равны нулю, то ранг матрицы принимается равным нулю. Отличный от нуля минор r-го порядка матрицы A (таких миноров у матрицы А может быть несколько, но все они имеют один и тот же порядок r) называется базисным минором матрицы А. Строки и столбцы, из которых построен базисный минор, называют базисными. Понятие ранга матрицы широко применяется в различных приложениях теории матриц.
Выделим в матрице А произвольно k строк. Пусть это будут строки
a1, а2, …, аk:
аα11, аα12, …, аα1n;
аα21, аα22, …, аα2n;
……………………
аαk1, аαk2, …, аαkn.
-16-
Если существуют такие числа λ1, λ2, …, λk, не все равные нулю, что для элементов некоторой другой, отличной от выделенной, строки i выполняются следующие соотношения:
(9)
то говорят, что i-я строка линейно выражается через строки
α1, α2, …, αk. В случае, если равенства (9) выполняются тогда и только тогда, когда все числа λ1, λ2, …, λk – нули, то говорят, что i-я строка линейно зависима от строк α1, α2, …, αk. Аналогичным образом можно ввести понятие линейной зависимости и линейной независимости между столбцами матрицы.
Теорема 1.2.(о базисном миноре) Любая строка матрицы А является линейной комбинацией её базисных строк.
Д о к а з а т е л ь с т в о. Предположим, что базисный минор матрицы (8) расположен в её верхнем левом углу, т.е. в первых r строках и первых r столбцах. Такое предположение не уменьшает общности рассуждения. Пусть k – номер любой строки матрицы А (k может принимать значения от 1 до m), а l – номер любого её столбца (l может принимать значения от 1 до n).
Рассмотрим следующий минор матрицы (8):
![]()
![]() a11 a12 …
a1r a1l
a11 a12 …
a1r a1l
a21 a22 … a11 a1l
∆ = ……………………… (10)
ar1 ar2 … arr arl
![]() ………………………
………………………
ak1 ak2 … akr akl
Если k
Похожие работы
... , придумать “свой метод", догадаться что-то прибавить и отнять, выделить полный квадрат, на что-то разделить и умножить и т.д. Если работа в поисках более рациональный способ решения систем линейных уравнений с двумя переменными - методом подстановки будет успешна, то практическая значимость будет очевидна. Список использованной литературы 1. Алгебра 8 класс. Н.Я. Виленкин. Москва, ...
... свести к вычислению четырех определителей третьего порядка. 3-ий учебный вопрос ТЕОРЕМА КРАМЕРА Применим рассмотренную теорию определителей к решению систем линейных уравнений. 1. Система двух линейных уравнений с двумя неизвестными. (3) Здесь х1, х2 – неизвестные; а11, …, а22 – коэффициенты при неизвестных, занумерованные двумя индексами, где первый ...
... . При этом собственно нахождение обратной матрицы – процесс достаточно трудоемкий и его программирование вряд ли можно назвать элементарной задачей. Поэтому на практике чаще применяют численные методы решения систем линейных уравнений. К численным методам решения систем линейных уравнений относят такие как: метод Гаусса, метод Крамера, итеративные методы. В методе Гаусса, например, работают над ...
... 10.4 9.7 9.7 -8.4 Результат вычислений по методу Гаусса x1 = 5.0000000000E+00 x2 = -4.0000000000E+00 x3 = 3.0000000000E+00 x4 = -2.0000000000E+00 2.2 Программа решения систем линейных уравнений по методу Зейделя 2.2.1. Постановка задачи. Требуется решить систему линейных алгебраических уравнений с вещественными коэффициентами вида a11x1 + a12x2 + … + a1nxn = b1 , a21x2 + ...
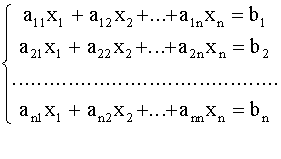
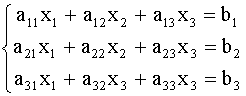





0 комментариев