Навигация
Субрегулярные растворы
1.2.2.2 Субрегулярные растворы
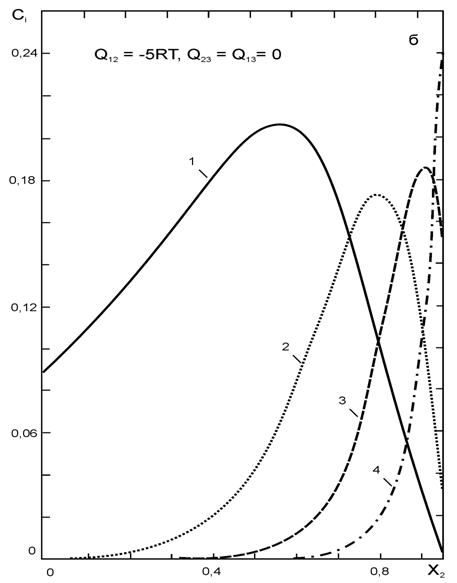
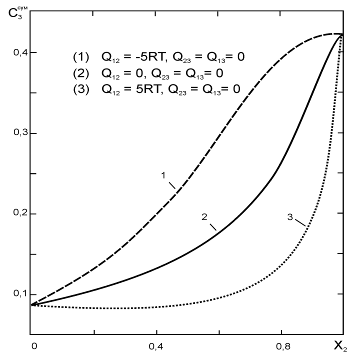
Одно из наиболее часто встречающихся противоречий заключатся в том, что реальные системы характеризуются обычно несимметричными зависимостями термодинамических характеристик от состава, а теория регулярных растворов предсказывает их симметрию. Чтобы устранить это расхождение теории с экспериментом был предложен один из усложненных вариантов модели, которых получил название субрегулярного раствора. Отличие этого раствора от регулярного заключается в том, что его энергия смешения не является константой, а изменяется в зависимости от состава и принимает значения от в чистом компоненте 1 до в компоненте 2. Это можно записать в виде уравнения:
(69)
.Так как , получим:
(70)
.Для определения парциальных теплот растворения воспользуемся формулой:
(71)
.В результате получим:
(72)
;(73)
.Остальные формулы теории субрегулярных бинарных растворов следуют из соответствующих формул для регулярных систем:
(74)
;(75)
;(76)
.Как видно из полученных уравнений, усложнение модели привело к тому, что в расчетные формулы входит теперь не один параметр (как в теории регулярных растворов), а два: и . Таким образом, повышение точности расчетов достигается в этом случае в результате увеличения количества исходной информации об объекте. Во многих случаях это не только приемлемо, но и необходимо для лучшего согласования расчетных данных с практическими. Чтобы найти необходимые для расчетов два параметра и в случае, когда неизвестны значения и , можно воспользоваться любыми двумя известными характеристиками: , , , или . Усложнение расчета сводится при этом к необходимости решения системы двух линейных уравнений типа рассмотренных выше. [6]
1.2.2.3 Квазирегулярные растворы
В случае квазирегулярного раствора поправка вводится как избыточная энтропия, связанная с теплотой образования раствора простым соотношением:
(77)
, .Из этого следуют важные расчетные формулы:
(78)
;(79)
.Из данного выражения можно вывести формулу для расчета температурной зависимости коэффициента активности по его значению при одной температуре. При обычном допущении имеем:
(80)
.Сопоставляя это выражение с выражением для регулярных растворов, видно, что при очень больших значениях (по сравнению с Т и 1873 К) формулы теории квазирегулярного раствора и регулярного раствора эквивалентны.
Как и для субрегулярных растворов, в формулы (78), (79) входят два параметра, в данном случае и , для определения которых необходимо не менее двух экспериментально полученных значений , или . Чтобы определить параметры, как и в предыдущем случае, необходимо решить систему двух линейных уравнений типа (78), (79). Указанное минимально необходимое количество исходных данных достаточно для выполнения расчета, но, как правило, не обеспечивает высокой точности получаемых результатов. В связи с этим для определения параметров используют обычно максимальное количество экспериментальных данных. Вычисления при этом выполняют методом наименьших квадратов.
Важным моментом в теории квазирегулярных растворов является то, обстоятельство, что параметр в первом приближении можно считать независящим от индивидуальных свойств компонентов раствора. Его можно заранее определить для широкого круга систем по имеющимся данным о теплотах и энтропиях образования некоторых из них. Формально представляет собой температуру, при нагреве до которой раствор приобретает свойства идеального. Это следует из того, что при формулы теории квазирегулярных растворов (78), (79) переходят в выражения для совершенного раствора. Расчеты показали, например, что корреляция между и в 90 растворах (жидких и твердых) на основе целого ряда растворителей при температуре от 293 до 1426 К удовлетворительно характеризуется одним значением параметра , равным 3000 К. Далекая экстраполяция зависимостей, полученных на основе модельных представлений, обычно не дает хороших результатов, поэтому не рекомендуется. [6]
36
2 Концентрационные уравнения для бинарных растворов с полной взаимной растворимостью
До недавнего времени в качестве математических моделей при исследовании термодинамических характеристик растворов применялись только интерполяционные уравнения:
«…пока не удается вывести в общем виде теоретически обоснованную формулу концентрационной зависимости термодинамических функций для реальных систем. В связи с этим при обработке экспериментальных данных применяются различные интерполяционные формулы [8] ».
Как известно, таким методом невозможно описать всего многообразия реально существующих металлических расплавов. Поэтому, в работе [9] впервые были выведены аналитические уравнения, связывающие термодинамические функции бинарного расплава с концентрацией его компонентов. Далее приведено краткое описание вывода.
Похожие работы
... впервые получены следующие результаты: · Разработана обобщенная координационно-кластерная модель для описания взаимодействий и расчета термодинамических характеристик раствора неметалла в расплаве из трех металлических компонентов. · Установлена связь между термодинамическими свойствами (коэффициентами термодинамической активности и параметрами взаимодействия компонентов первого порядка) и ...
... с кислородом, восстановлением - отнятие кислорода. С введением в химию электронных представлений понятие окислительно-восстановительных реакций было распространено на реакции, в которых кислород не участвует. В неорганической химии окислительно-восстановительные реакции (ОВР) формально могут рассматриваться как перемещение электронов от атома одного реагента (восстановителя) к атому другого ( ...
... молибдена и др. Эти материалы могут быть использованы в качестве легирующие компоненты для выплавки легированных чугуну и стали. Результаты исследований [11] показали, что использование отработанных никелевых катализаторов позволяет получать заготовку шихты с содержанием никеля 11 % и ванадию 3 % при одношлаковом режиме плавки. 1.2 Особенности редкофазной обновительной плавки. Выполненный ...
... Роквеллу НR Число твердости по Бринеллю НВ, кгс/мм2 Лабораторная работа № 3 Методы исследования качества, структуры и свойств металлов и сплавов Цель работы 1. Изучить сущность, возможности и методику выполнения основных видов макроструктурного и микроструктурного ...






0 комментариев