Навигация
Вывод концентрационных уравнений
2.1 Вывод концентрационных уравнений.
При образовании раствора относительная парциальная молярная энергия Гиббса одного из компонентов описывается уравнением:
(81)
;из данного уравнения активность компонента можно выразить следующим образом:
(82)
.Поскольку , то коэффициент активности:
(83)
.Задача заключается в том, чтобы величины , , а следовательно и представить как соответствующие концентрационные функции в компактной форме без каких–либо ограничений.
Рассмотрим парциальные молярные энтальпии компонентов бинарного раствора и , которые связаны между собой соотношением Гиббса – Дюгема:
(84)
;которое можно записать в следующей форме:
(84’)
.В результате определенных преобразований, аналитически получены концентрационные уравнения для парциальной молярной энтальпии компонентов в бинарном растворе с неограниченной растворимостью:
(85)
,(86)
.В этих уравнениях - парциальная молярная энтальпия при образовании бесконечно разбавленного раствора:
(87)
.Однако, в уравнениях (85) и (86) функции и выражены через «чужие» коэффициенты; т.е. парциальная молярная энтальпия первого компонента выражена через термодинамические характеристики второго и наоборот. Чтобы получить функции и через «свои» коэффициенты, обратимся к уравнению (84’). Подставляя в него выражение для из уравнения (86) и производя интегрирование, получим:
(88)
. Аналогичное выражение запишем и для :(89)
. Теперь парциальная молярная энтальпия выражена как концентрационная зависимость через величины, характеризующие природу соответствующего компонента. С учетом соотношения (87) уравнения (85) и (86) будут иметь вид:(90)
;(91)
.Из этих уравнений следует равенство:
(92)
,связывающее между собой коэффициенты и . И вообще, уравнения (90)–(92) позволяют находить соответствующие постоянные величины для одного компонента, если они известны для другого.
Все приведенные выше рассуждения справедливы и для другой термодинамической функции . Поэтому, сразу запишем для нее конечное выражение:
(93)
.Зная концентрационные выражения для и , можно написать соответствующее уравнение для парциальной молярной свободной энергии Гиббса:
(94)
.Для активности компонента в растворе данное уравнение перепишется так:
(95)
,г
(96)
де ; .Выражение (95) позволяет описать экспериментальные данные зависимости активности компонента от состава бинарного раствора. Перепишем его следующим образом:
(97)
Разделив левую и правую части данного уравнения на и имея в виду, что (о функции скажем далее), запишем выражение:
(98)
.Из уравнения (98) видно, что при :
(99)
,а
(100)
при : .2.2 Функция .
Функция впервые была введена Л.С. Даркеном и Р.В. Гурри [2] для упрощения интегрирования уравнения Гиббса-Дюгема при определении активности одного компонента бинарной системы из известной активности другого компонента. Они же показали, что функция i для металлических расплавов имеет прямолинейный характер. В работах других исследователей также утверждается, что при нанесении на график величин в функции (1 - xi) экспериментальные точки должны ложиться на прямую.
На рисунке 5 представлены результаты вычисления функции для различных систем в зависимости от концентрации компонента в расплаве. Для каждой системы имеем две линии – это и . Цифрами обозначены точки пересечения этих линий в расплавах:
1-(Fe – Si); 2-(Fe – Al); 3-(Fe – V); 4-(Fe – Co); 5-(Fe – Mn); 6-(Fe – Cr) и 8-(Fe – Sn). Для каждой точки пересечения линий характерно своё значение . Значения в точках пересечения обозначены через . Из рисунка 5 видно, что чем дальше система от идеальности, тем больше угол между рассматриваемыми прямыми. Пересекаются линии всех систем примерно при одной и той же концентрации компонентов в расплаве, очень близкой к значению xi=0,25 (среднее значение xi для рассматриваемых систем равно 0,251). Угол между прямыми можно характеризовать величиной , т.е. абсолютным значением разности функций при xi=1 для конкретного компонента любой системы. Это позволяет предположить, что между величиной и функцией должна существовать определенная связь. Она показана на рисунке 6. Из рисунка видно, что зависимость между и может быть описана в общем виде уравнением параболы второй степени, а именно:
.
Для положительных и отрицательных значений уравнения параболы отличаются, их примерный вид приведен на этом же рисунке. Это объясняется тем, что растворы с положительным и отрицательным отклонением от закона Рауля по своей природе различаются: для систем с отрицательным отклонением никаких ограничений нет, в то время как для систем с положительным отклонением ограничения существуют. Уравнения на рисунке 6 могут быть уточнены при нанесении на него дополнительных данных.
Итак, в данной главе мы привели концентрационные уравнения, связывающие термодинамические характеристики с составом бинарного раствора с неограниченной растворимостью компонентов. В этих уравнениях коэффициенты и , наряду с другими величинами (, , T, xi), определяют степень отклонения реального раствора от идеального.
Задача исследователя заключается в том, чтобы по имеющимся экспериментальным данным определить неизвестные величины , , и (при известной температуре и концентрации компонентов), входящие в уравнение (98). При любой методике вычисления этих величин в первую очередь определяются численные значения и , а также их знаки, и лишь затем находятся и . Поэтому следующая глава нашей работы посвящена вопросам определения коэффициентов и .
44
Похожие работы
... впервые получены следующие результаты: · Разработана обобщенная координационно-кластерная модель для описания взаимодействий и расчета термодинамических характеристик раствора неметалла в расплаве из трех металлических компонентов. · Установлена связь между термодинамическими свойствами (коэффициентами термодинамической активности и параметрами взаимодействия компонентов первого порядка) и ...
... с кислородом, восстановлением - отнятие кислорода. С введением в химию электронных представлений понятие окислительно-восстановительных реакций было распространено на реакции, в которых кислород не участвует. В неорганической химии окислительно-восстановительные реакции (ОВР) формально могут рассматриваться как перемещение электронов от атома одного реагента (восстановителя) к атому другого ( ...
... молибдена и др. Эти материалы могут быть использованы в качестве легирующие компоненты для выплавки легированных чугуну и стали. Результаты исследований [11] показали, что использование отработанных никелевых катализаторов позволяет получать заготовку шихты с содержанием никеля 11 % и ванадию 3 % при одношлаковом режиме плавки. 1.2 Особенности редкофазной обновительной плавки. Выполненный ...
... Роквеллу НR Число твердости по Бринеллю НВ, кгс/мм2 Лабораторная работа № 3 Методы исследования качества, структуры и свойств металлов и сплавов Цель работы 1. Изучить сущность, возможности и методику выполнения основных видов макроструктурного и микроструктурного ...



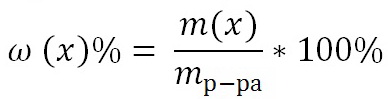
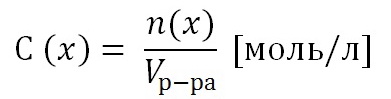



0 комментариев