Навигация
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ И
3 ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ И
К
(101)
ак было сказано выше, коэффициенты и определяют степень отклонения раствора от идеальности. По условиям вывода диапазон значений этих коэффициентов одинаков и равен:В бинарных растворах коэффициенты и , равно как и коэффициенты и , связаны между собой соотношениями:
(102)
,(103)
.Коэффициенты и противоположны по знаку. Противоположные знаки также имеют и . Определить численное значение коэффициентов и можно двумя методами: математическим и графическим.
3.1 Математический метод.
При чисто математическом подходе, основываясь на экспериментальных данных, получим систему четырех уравнений типа (98), решение которой (например, методом наименьших квадратов) позволяет найти значения всех неизвестных величин: , , и . В процессе решения возникает ситуация, когда надо определить, какой из корней квадратного уравнения коэффициент , а какой –, т.е. нужно знать знаки коэффициентов. Способ определения знака мы рассмотрим ниже, в этой главе.
Стоит сразу отметить весьма низкую точность результатов, рассчитанных математическим методом. Причины этого:
1 – абсолютные значения величин Ai и Bi отличаются на порядок, а иногда и на два, от абсолютных значений и , что является причиной погрешности при решении.
2 – недостаточная точность экспериментальных данных; этот пункт рассмотрим подробнее.
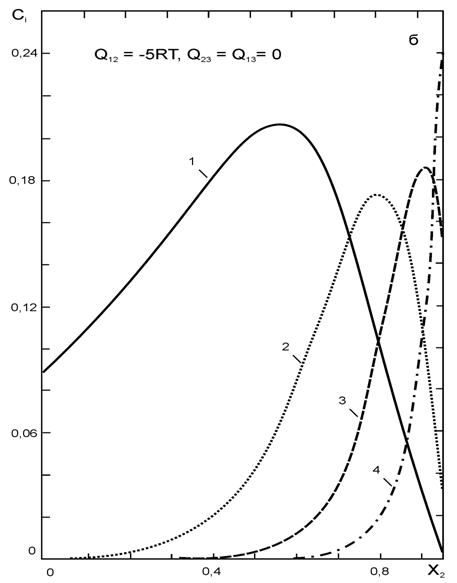
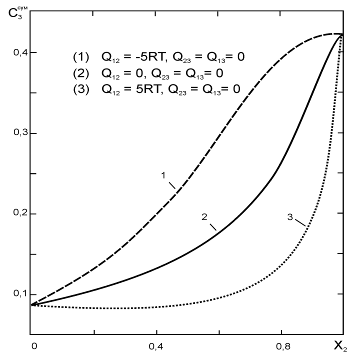
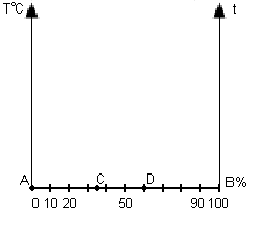
Часто в термодинамических исследованиях экспериментально пользуясь различными методиками определяют связь активности одного из компонентов с его концентрацией в растворе. При этом график функции имеет следующие особенности. Кривая активности в точках и как бы жестко закреплена; при этом значения ai равны нулю и единице соответственно. Однако, в интервале 0Рост. , то можно записать:
(124)
здесь - коэффициент испарения, учитывающий прежде всего состояние поверхности;
М – молекулярный вес испаряющегося металла.
Уравнение (124) известно как классическая формула Кнудсена и выведено на основании молекулярно – кинетической теории при следующих допущениях:
отсутствуют столкновения молекул между собой как в объеме эффузионной камеры, так и в области эффузионного отверстия;
длина свободного пробега частицы велика по сравнению с размерами эффузионного отверстия;
все атомы, попавшие в эффузионное отверстие, проходят через него, не изменяя направления движения, так как края отверстия бесконечно тонки.
Первые два условия обычно выполняются, если давление пара не превышает 1,3 – 13,3 Па, а радиус отверстия не более 1 мм.
По исходным данным построим графики функций и (рисунки 32 и 33). На этих же рисунках проведены прямые линии, полученные путем обработки первичных литературных данных в соответствии с уравнением прямой.
5.3.2 Корректировка исходных данных.
Приведем вычисление коэффициентов в уравнении прямой для вольфрама (таблица 18).
Таблица 18 – Необходимые параметры для вычисления коэффициентов в уравнении прямой для функции .
| Численные значения | ||||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 4,5 | |
| 0,01 | 0,04 | 0,09 | 0,16 | 0,25 | 0,36 | 0,49 | 0,64 | 0,81 | 2,85 | |
| -0,8557 | -0,9341 | -1,1592 | -1,5372 | -1,9121 | -2,6924 | -3,7386 | -5,9723 | -3,0459 | -21,8475 | |
| -0,0856 | -0,1868 | -0,3478 | -0,6149 | -0,956 | -1,6154 | -2,617 | -4,7778 | -2,7413 | -13,9426 | |
Вычисления:
.
Таким образом, для функции получено выражение:
(125)
Уравнение для , полученное аналогичным образом имеет вид:
(126)
Исходные данные, скорректированные в соответствии с уравнением (125) приведены в таблице 19.
Таблица 19 – Скорректированные исходные данные для вольфрама.
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
| -0,4183 | -0,9256 | -1,422 | -1,939 | -2,446 | -2,953 | -3,46 | -3,997 | -4,473 | |
| 0,0712 | 0,1106 | 0,1487 | 0,199 | 0,2713 | 0,374 | 0,5127 | 0,6826 | 0,8606 |
По данным таблицы 19 построим рисунок 34, на котором изображена функция: . Из этого рисунка получаем: ; ; . Коэффициент отклонения площади от идеальности равен:
.
Графическим методом определены:
и .
Из уравнения: ,
определены: и .
Далее, по уравнению (98) вычислим другие термодинамические характеристики для компонентов расплава W – Pd.
5.1.3 Вычисление значений Аi, Bi, и .
Термодинамические характеристики вольфрама в расплаве W – Pd.
Термодинамические характеристики палладия в расплаве W – Pd.
По приведенным термодинамическим характеристикам вычислим значения основных термодинамических характеристик компонентов в расплаве W – Pd при различных их концентрациях (таблицы 20 и 21).
По данным этих таблиц построены графики (рисунки 35 и 36).
Вывод: Показана применимость концентрационных уравнений для термодинамического описания бинарных металлических расплавов со знакопеременным отклонением от идеальности.
| Функция | Концентрация вольфрама в расплаве - xW | ||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
| 0,1286 | -0,399 | -0,918 | -1,429 | -1,934 | -2,433 | -2,927 | -3,417 | 3,904 | -4,389 | -4,872 | |
| 0,1286 | -0,323 | -0,587 | -0,700 | -0,696 | -0,608 | -0,468 | -0,308 | -0,156 | -0,044 | 0,00 | |
| 1,137 | 0,724 | 0,556 | 0,496 | 0,498 | 0,544 | 0,626 | 0,735 | 0,855 | 0,957 | 1,00 | |
| 0,00 | 0,0724 | 0,1112 | 0,1489 | 0,1994 | 0,2722 | 0,3756 | 0,5147 | 0,6843 | 0,8614 | 1,00 | |
| -253,26 | -207,76 | -166,28 | -128,97 | -96,01 | -67,57 | -43,84 | -25,00 | -11,27 | -2,86 | 0,00 | |
| -129,4 | -102,6 | -79,4 | -59,5 | -42,86 | -29,20 | -18,30 | -10,10 | -4,40 | -1,10 | 0,00 | |
Таблица 20 – Вычисленные термодинамические характеристики вольфрама в расплаве W – Pd при Т=1873 К.
| Функция | Концентрация палладия в расплаве - xPd | ||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
| -1,823 | -1,402 | -0,977 | -0,548 | -0,115 | 0,325 | 0,770 | 1,223 | 1,684 | 2,153 | 2,633 | |
| -1,823 | -1,135 | -0,625 | -0,269 | -0,041 | 0,081 | 0,123 | 0,110 | 0,067 | 0,022 | 0,00 | |
| 0,167 | 0,321 | 0,535 | 0,764 | 0,960 | 1,085 | 1,131 | 0,112 | 1,070 | 1,022 | 1,00 | |
| 0,00 | 0,0321 | 0,107 | 0,2293 | 0,3838 | 0,5423 | 0,6787 | 0,7814 | 0,8557 | 0,9196 | 1,00 | |
| -229,61 | -183,40 | -142,92 | -107,94 | -78,20 | -53,60 | -33,87 | -18,81 | -8,25 | -2,04 | 0,00 | |
| -101,2 | -83,5 | -67,2 | -52,5 | -39,3 | -27,8 | -18,2 | -10,4 | -4,7 | -1,2 | 0,0 | |
Таблица 21 – Вычисленные термодинамические характеристики палладия в расплаве W – Pd при Т=1873 К.
114
6 СИСТЕМЫ С РАЗЛИЧНЫМ ОТКЛОНЕНИЕМ ОТ ИДЕАЛЬНОСТИ
6.1 Системы с положительным отклонением от идеальности.
6.1.1 Система Fe – Mn.
Исходные данные. Исходные данные, взятые из разных источников, представлены в таблице 22.
Таблица 22 – Исходные данные для марганца.
| Функция | xMn | ||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
| aMn[21] | 0,124 | 0,242 | 0,364 | 0,46 | 0,54 | 0,634 | 0,708 | 0,81 | 0,905 |
| aMn [25] | 0,137 | 0,257 | 0,363 | 0,46 | 0,552 | 0,638 | 0,725 | 0,813 | 0,904 |
| aMn [26] | 0,122 | 0,239 | 0,351 | 0,455 | 0,552 | 0,644 | 0,731 | 0,817 | 0,905 |
| aMn средн. | 0,128 | 0,246 | 0,359 | 0,460 | 0,548 | 0,639 | 0,721 | 0,813 | 0,905 |
| 0,01 | 0,04 | 0,09 | 0,16 | 0,25 | 0,36 | 0,49 | 0,64 | 0,81 | |
| 0,305 | 0,323 | 0,366 | 0,388 | 0,367 | 0,394 | 0,328 | 0,403 | 0,554 | |
| 0,030 | 0,065 | 0,11 | 0,155 | 0,183 | 0,236 | 0,230 | 0,322 | 0,499 | |
По этим данным построим график зависимости функции от концентрации марганца в расплаве (рисунок 37).
Корректировка данных.
Уравнение прямой для функции будет выглядеть так:
(127)
Таблица 23 – Скорректированные исходные данные для марганца.
| 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
| 0,2842 | 0,304 | 0,323 | 0,342 | 0,362 | 0,381 | 0,400 | 0,420 | 0,439 | 0,458 | 0,478 | |
| 0,00 | 0,128 | 0,246 | 0,355 | 0,456 | 0,550 | 0,640 | 0,727 | 0,814 | 0,904 | 1,00 |
Термодинамические характеристики компонентов. Вычисленные термодинамические характеристики марганца в расплаве Fe – Mn :
| Функция | Концентрация марганца в расплаве - xMn | |||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | ||
| р а с ч е т | 0,2842 | 0,304 | 0,324 | 0,343 | 0,363 | 0,382 | 0,401 | 0,421 | 0,440 | 0,459 | 0,478 | |
| 0,2842 | 0,246 | 0,207 | 0,168 | 0,131 | 0,095 | 0,064 | 0,038 | 0,018 | 0,005 | 0,00 | ||
| 1,329 | 1,279 | 1,23 | 1,183 | 1,139 | 1,10 | 1,066 | 1,039 | 1,018 | 1,005 | 1,00 | ||
| 0,00 | 0,128 | 0,246 | 0,355 | 0,456 | 0,55 | 0,64 | 0,727 | 0,814 | 0,904 | 1,00 | ||
| опыт | - - - - | 0,305 | 0,323 | 0,366 | 0,388 | 0,367 | 0,394 | 0,328 | 0,403 | 0,554 | - - - - | |
| 0,00 | 0,128 | 0,246 | 0,359 | 0,460 | 0,548 | 0,639 | 0,721 | 0,813 | 0,905 | 1,00 | ||
Таблица 24 – Вычисленные термодинамические характеристики марганца в расплаве Fe – Mn при Т=1873 К.
Таблица 25 – Вычисленные термодинамические характеристики железа в расплаве Fe – Mn при Т=1873 К.
| Функция | Концентрация железа в расплаве - xFe | |||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | ||
| р а с ч е т | 0,3814 | 0,362 | 0,343 | 0,324 | 0,305 | 0,285 | 0,266 | 0,246 | 0,227 | 0,207 | 0,1877 | |
| 0,3814 | 0,293 | 0,220 | 0,159 | 0,110 | 0,071 | 0,043 | 0,022 | 0,009 | 0,002 | 0,00 | ||
| 1,463 | 1,341 | 1,246 | 1,172 | 1,116 | 1,074 | 1,043 | 1,022 | 1,009 | 1,002 | 1,00 | ||
| 0,00 | 0,134 | 0,249 | 0,352 | 0,446 | 0,537 | 0,626 | 0,716 | 0,807 | 0,902 | 1,00 | ||
| опыт | н е т | |||||||||||
| д а н н ы х | ||||||||||||
Похожие работы
... впервые получены следующие результаты: · Разработана обобщенная координационно-кластерная модель для описания взаимодействий и расчета термодинамических характеристик раствора неметалла в расплаве из трех металлических компонентов. · Установлена связь между термодинамическими свойствами (коэффициентами термодинамической активности и параметрами взаимодействия компонентов первого порядка) и ...
... с кислородом, восстановлением - отнятие кислорода. С введением в химию электронных представлений понятие окислительно-восстановительных реакций было распространено на реакции, в которых кислород не участвует. В неорганической химии окислительно-восстановительные реакции (ОВР) формально могут рассматриваться как перемещение электронов от атома одного реагента (восстановителя) к атому другого ( ...
... молибдена и др. Эти материалы могут быть использованы в качестве легирующие компоненты для выплавки легированных чугуну и стали. Результаты исследований [11] показали, что использование отработанных никелевых катализаторов позволяет получать заготовку шихты с содержанием никеля 11 % и ванадию 3 % при одношлаковом режиме плавки. 1.2 Особенности редкофазной обновительной плавки. Выполненный ...
... Роквеллу НR Число твердости по Бринеллю НВ, кгс/мм2 Лабораторная работа № 3 Методы исследования качества, структуры и свойств металлов и сплавов Цель работы 1. Изучить сущность, возможности и методику выполнения основных видов макроструктурного и микроструктурного ...






0 комментариев