Навигация
Закон электромагнитной индукции
2.3. Закон электромагнитной индукции.
Устанавливает в интегральной форме зависимость ЭДС, наведенной в контуре от магнитного потока. Сформулировал закон электромагнитной индукции Фарадей.
Э = 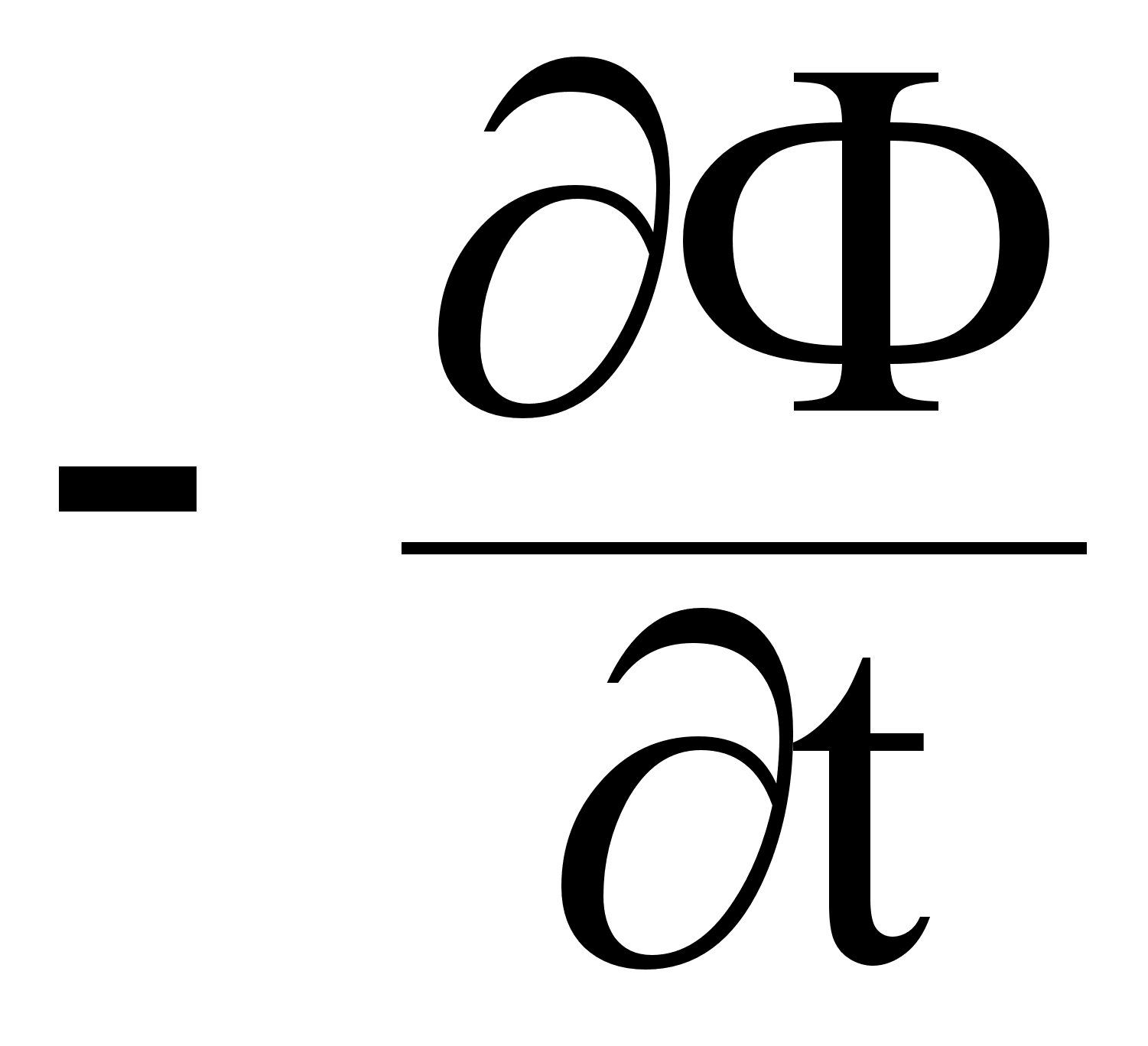 (2.3.1.)
(2.3.1.)
Э = ![]() Е
dl - циркуляция
вектора Е по
Е
dl - циркуляция
вектора Е по
L замкнутому контуру L.
Ф = В dS - поток вектора В
S
Площадка S опирается на контур L
![]()
![]()
![]() E
dl = -
E
dl = - 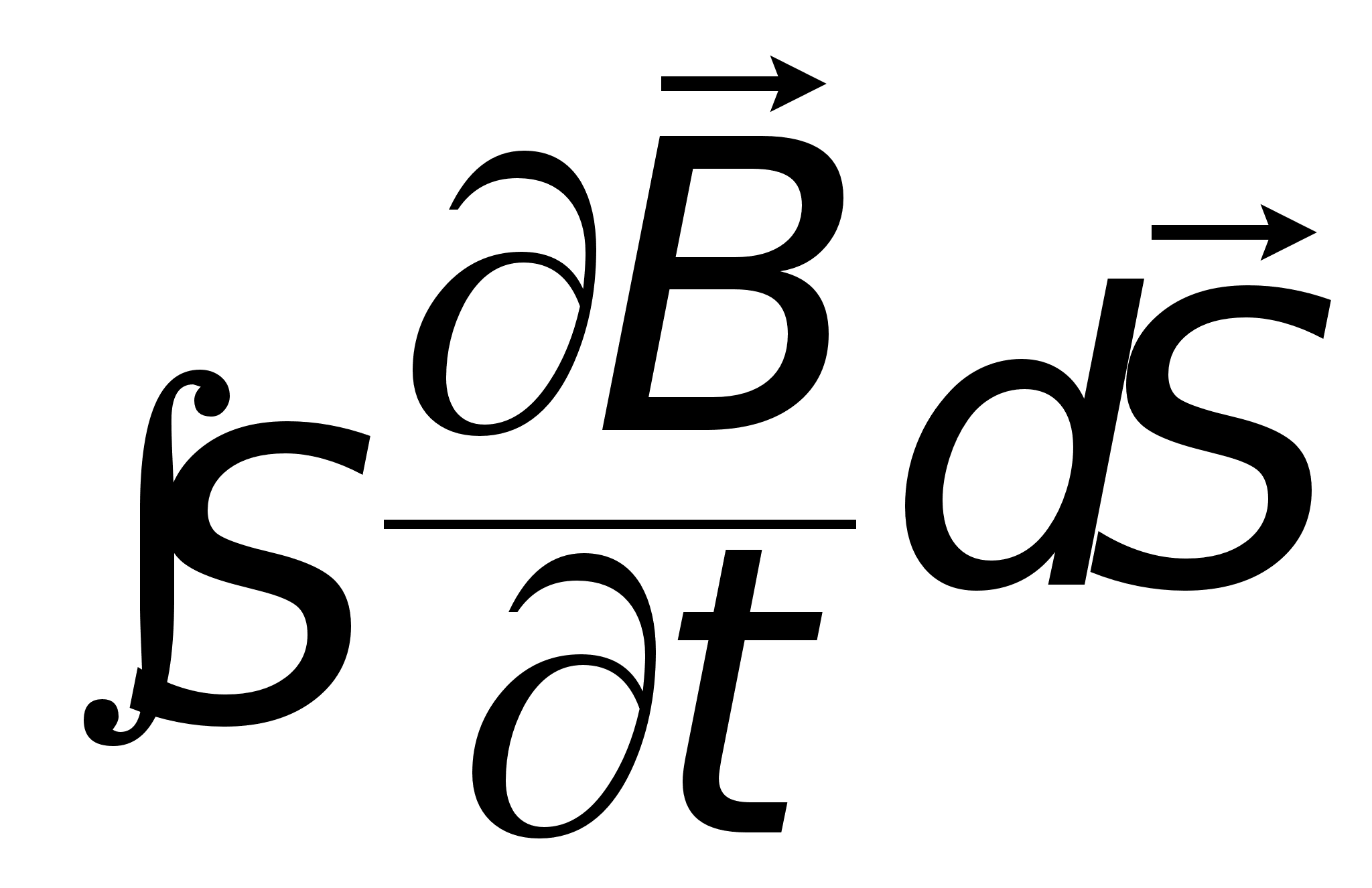 (2.3.2.)
(2.3.2.)
L
Знак (-) говорит о том, что возникшая в контуре ЭДС будет создавать переменное магнитное поле, которое препятствует направлению основного поля, которое вызвало ЭДС.
2.4. Закон сохранения заряда.
В замкнутой системе при любых процессах полный заряд остается неизменным. Если заряд остается неизменным, значит ничего не вышло за пре делы. Если заряд меняется, значит возникает ток:

I
= Q
/ t
; I = ![]() пр
dS (2.4.1.)
пр
dS (2.4.1.)
S
Q = v dV; (2.4.2.)
v
![]() пр
dS = -
пр
dS = -
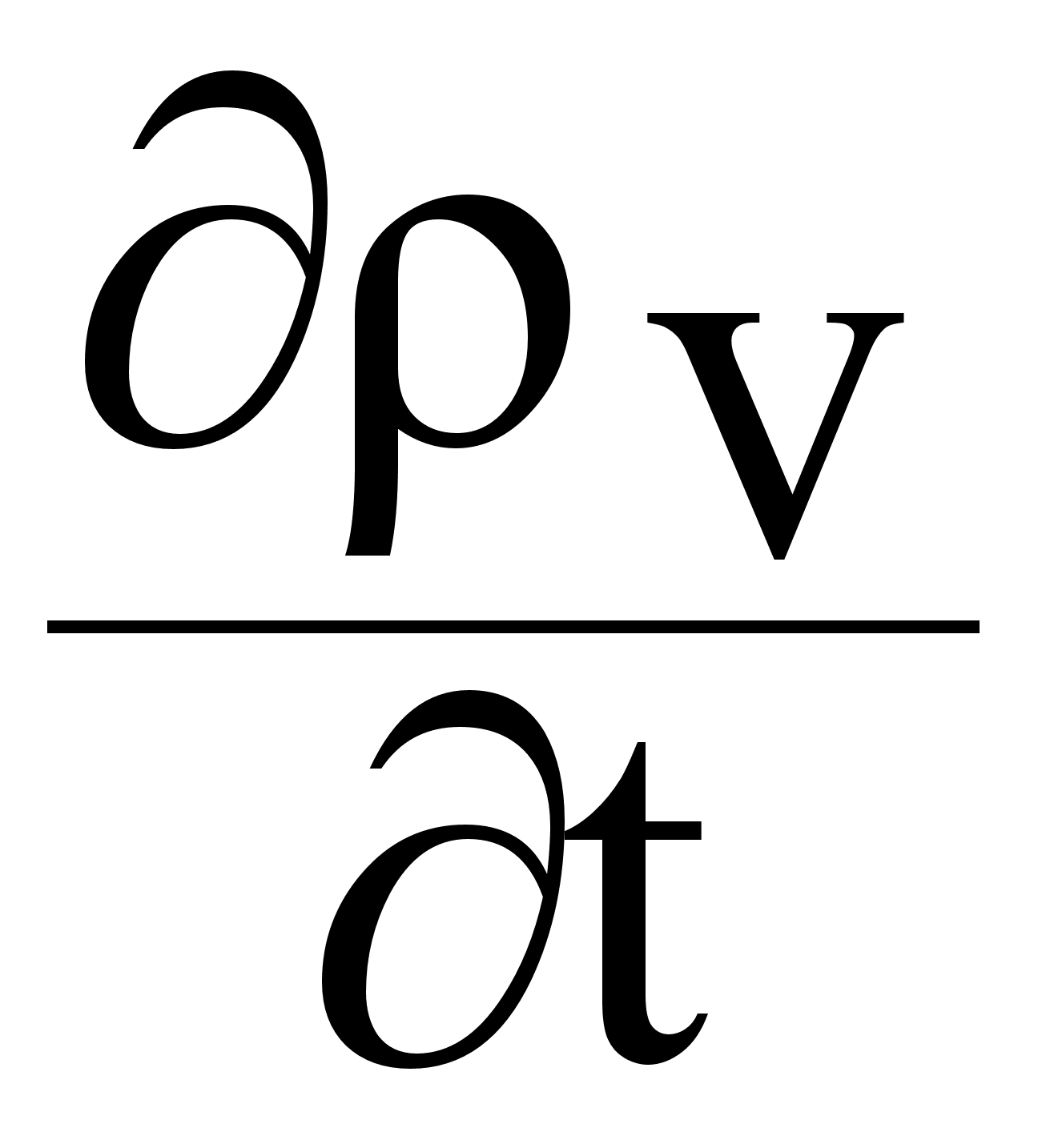 dV - уравнение
dV - уравнение
sv непрерывности полного тока.
6
Лекция 3
Уравнения Максвелла. Дифференциальные
уравнения электромагнитного поля.
3.1. Первое уравнение Максвелла.
3.2. Второе уравнение Максвелла.
3.3. Третье уравнение Максвелла.
3.4. Четвертое уравнение Максвелла.
3.5. Закон сохранения заряда в дифференциальной форме.
3.6. Таблица уравнений ЭМП.
1. Интегральные уравнения не позволяют получать информацию об электромагнитных процессах в каждой точке пространства. Они дают усредненные решения полей в пространстве.
2. Хорошо развитый аппарат математических решений позволят переходить от интегральной формы к дифференциальным решениям.
Впервые переход от интегральных уравнений к дифференциальным сделал Максвелл.
3.1. Первое уравнение Максвелла является дифференциальной формулировкой закона полного тока:
![]() H
dl = Iпол ; Iпол
= Iпр
+ Iсм
H
dl = Iпол ; Iпол
= Iпр
+ Iсм
L
Iпол = полн dS ; пол = пр + см (3.1.1.)
S
S - опирается на контур L.
![]() H
dl =
полн
dS (3.1.2.)
H
dl =
полн
dS (3.1.2.)
L S
Используем теорему Стокса:
![]() H
dl =
rot H dS =
полн
dS (3.1.3.)
H
dl =
rot H dS =
полн
dS (3.1.3.)
L S S
Равенство сохраняет силу по любой поверхности, опирающейся на контур L, отсюда следует, что подынтегральные функции равны.
rot H = полн ; пр = E - дифференциальная форма закона Ома.
см
= ![]()
rot H =
E + ![]() - первое уравнение
Максвелла.
(3.1.4.)
- первое уравнение
Максвелла.
(3.1.4.)
Физический смысл 1-го уравнения Максвелла.
Источниками вихревых магнитных полей являются токи проводимости и токи смещения.
3.2. Второе уравнение Максвелла является дифференциальной формулировкой закона электромагнитной индукции:
![]() E
dl = -
E
dl = -
 dS
; (3.2.1.)
dS
; (3.2.1.)
L S
rot E dS = -  dS (3.2.2.)
dS (3.2.2.)
S S
rot E = -  - второе уравнение
Максвелла.
(3.2.3.)
- второе уравнение
Максвелла.
(3.2.3.)
Физический смысл. Вихревое электрическое поле создается переменным магнитным полем.
Похожие работы
... в пространстве. Утверждение о существовании электромагнитных волн является непосредственным следствием решения системы уравнений Максвелла. Согласно этой теории следует, что переменное электромагнитное поле распространяется в пространстве в виде волн, фазовая скорость которых равна: где - скорость света в вакууме, , - электрическая и магнитная постоянные, , - соответственно диэлектрическая ...
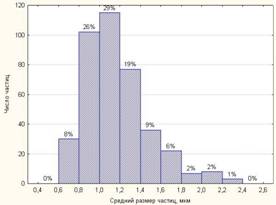
... поле – 2. Исследованиями установлено, что воздействие ультразвуковых колебаний на исходный порошок через жидкую среду приводит к его некоторому измельчению за счет разрушения агломератов. Сравнение микроструктуры керамики ЦТБС-3М, полученной различными методами, позволяет сделать вывод, что наименьшая пористость наблюдается у образцов, синтезированных из пресс-заготовок, полученных из порошка, ...
... переменного тока проводимости или тока смещения, где длина волны зависит от частоты колебания. Любой электрический ток, согласно электродинамике, всегда замкнут. Поэтому продольные электромагнитные волны всегда замкнуты независимо от того, представляют они переменный электрический ток проводимости или смещения. Продольные электрические возмущения поля имеют продольную ориентацию электрического ...
... потока Ф0 ...» Физические величины (справочник). 1991. С.1234. «Собственно говоря, постоянной Планка называется коэффициент пропорциональности ...» Квантовая физика. И.Е.Иродов. 2001. С.11. Электромагнитная волна де Бройля, как и фотон, представляет электромагнитный квант, состоящий из кванта электрического потока (заряда) и кванта магнитного потока. Длина волны де Бройля и энергия ...
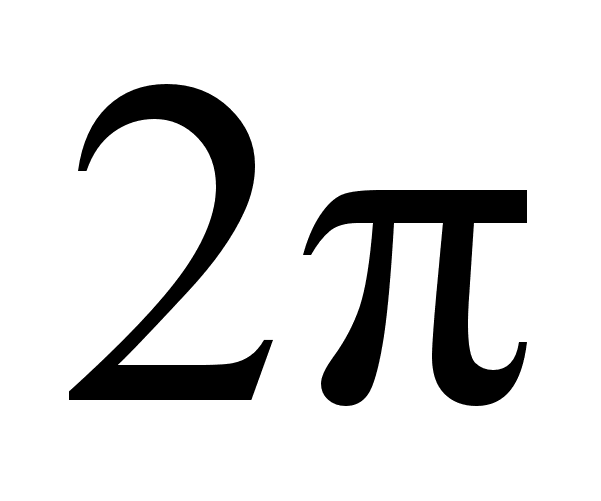
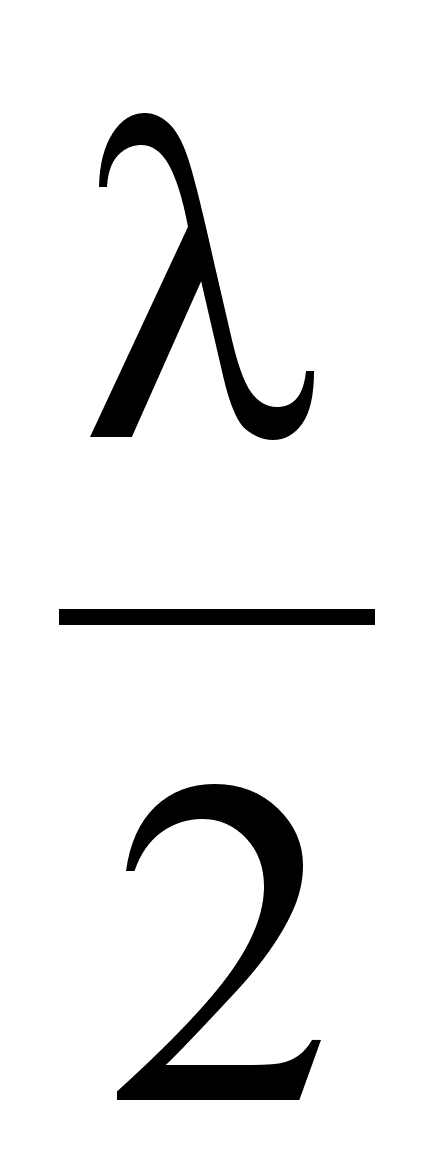
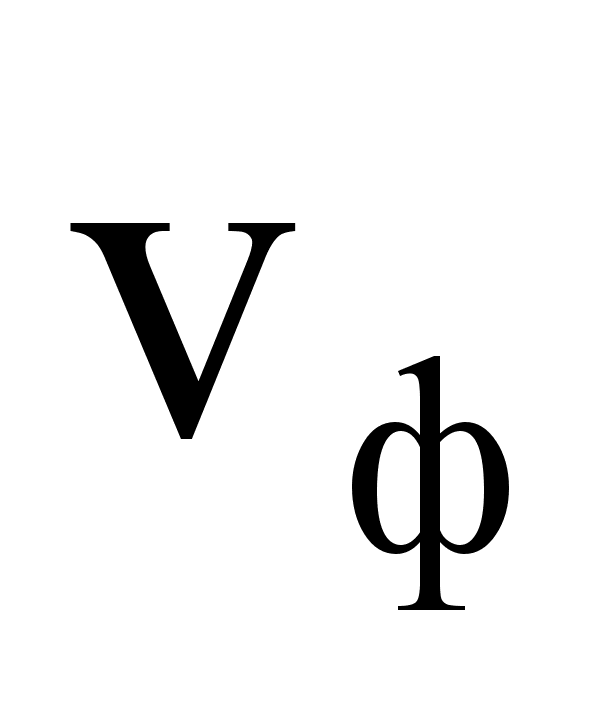


0 комментариев