Навигация
Уравнение баланса энергии
4.1. Уравнение баланса энергии.
Баланс энергии ЭМП является следствием закона сохранения энергии для ЭМП. Выберем произвольный объем, ограниченный поверхностью S, внутри находятся источники ЭМП.
С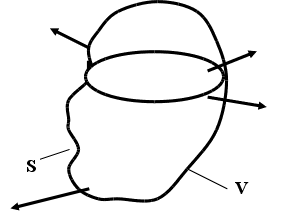 читаем,
что мощность
источников
нам известна,
обозначим ее Рст
(сторонняя).
Природа сторонних
источников
не рассматривается.
Выясним,
на какие процессы
расходуется
Рст :
читаем,
что мощность
источников
нам известна,
обозначим ее Рст
(сторонняя).
Природа сторонних
источников
не рассматривается.
Выясним,
на какие процессы
расходуется
Рст :
1) Часть Рст преобразуется в другие виды энергии (тепло и т.д.). Это мощность Рпот.
2) Внутри V могут
находиться
элементы, которые
запасают энергию.
Для характеристики
этих процессов
вводится понятие
плотности
энергии ЭМП WЭМ,
удельная мощность
 По
всему объему:
По
всему объему:
РЭМ
=  dV (4.1.1.)
dV (4.1.1.)
V
РЭМ - мощность расходуемая на изменение накопленной внутри объема энергии ЭМП.
3) С ЭМП связаны процессы переноса энергии.
![]() Эта часть
Р называют
излучаемой
Ризл.
Для характеристики
таких процессов
введем понятие
плотности
энергии переносимой
ЭМП через единичную
поверхность
за единицу
времени в
перпендикулярном
поверхности
направлении.
Эта величина
получила название
вектора Пойнтинга
П и характеризует
количество
энергии переносимой
через единичную
площадку за
единицу времени
поверхности:
Эта часть
Р называют
излучаемой
Ризл.
Для характеристики
таких процессов
введем понятие
плотности
энергии переносимой
ЭМП через единичную
поверхность
за единицу
времени в
перпендикулярном
поверхности
направлении.
Эта величина
получила название
вектора Пойнтинга
П и характеризует
количество
энергии переносимой
через единичную
площадку за
единицу времени
поверхности:
П [Вт/м2]
Мощность излучения:
Ризл
=![]() П
dS (4.1.2.)
П
dS (4.1.2.)
S
В силу закона сохранения энергии имеем:
(4.1.3.)
Рст
= Рпот
+
(W
/ t)
dV + ![]() П
dS - уравнение
баланса энергии.
П
dS - уравнение
баланса энергии.
VS
Пример:

4.2. Теорема Пойнтинга.
Теорема Пойнтинга устанавливает количественную связь между векторными характеристиками полей и отдельными составляющими баланса энергии ЭМП.
Для установления этой связи воспользуемся уравнениями Максвелла:
H rot E = -  (4.2.1.)
(4.2.1.)
E rot H = см +пр + ст (4.2.2.)
Вычтем (4.2.2.) из (4.2.1.):
H rot E - E rot H = - H - смЕ
- прЕ
- стЕ (4.2.3.)
H - смЕ
- прЕ
- стЕ (4.2.3.)
(div [a x b] = b rot a - a rot b) тождество (4.2.4.)
div[ E x H] = - ( H
+
H
+  E)
- прЕ
- стЕ (4.2.5.)
E)
- прЕ
- стЕ (4.2.5.)
Закон сохранения энергии это интегральное соотношение. Поэтому выполним интегрирование последнего уравнения по объему V:
div [E H] dV = -
( H
+
H
+  E)
dV -
E)
dV -
V v
- пр E dV - ст E dV (4.2.6.)
V V
по теореме Остроградского-Гаусса:
![]()
![]()
![]()
![]()
![]() div [E x H] dV =
div [E x H] dV = ![]() [E
x H] dS (4.2.7.)
[E
x H] dS (4.2.7.)
V S
Упростим выражение под знаком объемного интеграла:
 H
+
H
+  E
=
E
= ![]() (aH)
H +(
(aH)
H +(![]() )
(aE)
E =
)
(aE)
E =
 (4.2.8)
(4.2.8)
- (4.2.9)
(4.2.9)
Сравним последнее уравнение с составляющими баланса энергии ЭМП (4.1.2.):
Рст = ст Е dV знак (-) говорит о том,
v что энергия расходуется.
Рпотерь = пр Е dV
V
Wэм
= 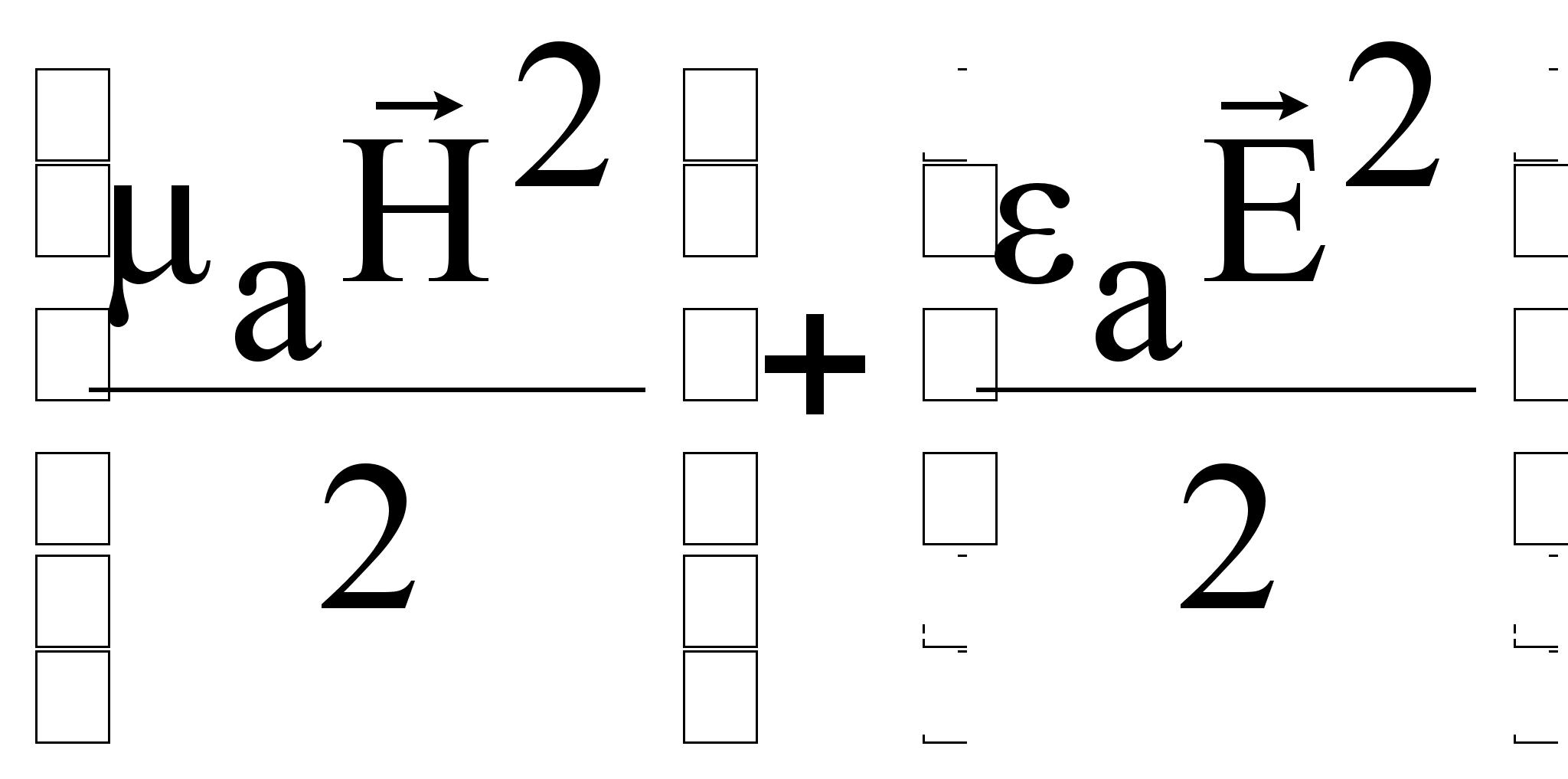
Wэ
=  ; Wм =
; Wм =

П = [E x H] (4.2.10.)
3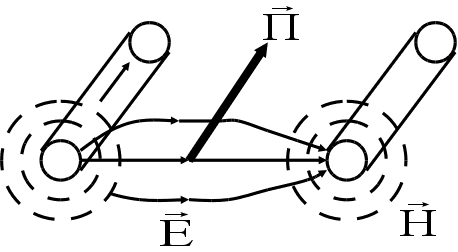 .
Некоторые
примеры.
.
Некоторые
примеры.
![]()
![]()
![]()
Д![]()
![]()
![]()
![]() ля определения направления переноса энергии необходимо
определить
направления П. В соответствии
с правилами векторного произведения направление
вектора П,
перпендикулярно
плоскости
векторов Е и
Н. Основная
энергия, переносимая
вдоль линии,
распределена
вне проводов.
Можно показать,
что энергия,
поступающая
внутрь
провода в точности равна джоулевым
потерям.
ля определения направления переноса энергии необходимо
определить
направления П. В соответствии
с правилами векторного произведения направление
вектора П,
перпендикулярно
плоскости
векторов Е и
Н. Основная
энергия, переносимая
вдоль линии,
распределена
вне проводов.
Можно показать,
что энергия,
поступающая
внутрь
провода в точности равна джоулевым
потерям.![]()


4
Лекция 5
Классификация ЭМП
5.1. Статические поля.
5.2. Стационарные поля.
5.3. Квазистационарные поля.
5.4. Относительность свойств реальных сред.
5.5. Быстропеременные поля.
В основе классификации ЭМП лежат 2 критерия:
Зависимость полей от времени.
Соотношение между токами проводимости и смещения.
5.1. Статические поля.
Статические поля не зависят от времени :
![]() =
0 см
= 0
=
0 см
= 0
Заряды неподвижные пр = 0.
Уравнения Максвелла:
1. rot H = 0; 2. rot E = 0
3. div B = 0; 4. div D =
B = a H; D = a E (5.1.1.)
В статических полях электрические и магнитные явления проявляют себя независимо. Уравнения Максвелла распадаются на 2 системы:
rot H = 0 rot E = 0
div B =0 div D = (5.1.2.)
Похожие работы
... в пространстве. Утверждение о существовании электромагнитных волн является непосредственным следствием решения системы уравнений Максвелла. Согласно этой теории следует, что переменное электромагнитное поле распространяется в пространстве в виде волн, фазовая скорость которых равна: где - скорость света в вакууме, , - электрическая и магнитная постоянные, , - соответственно диэлектрическая ...
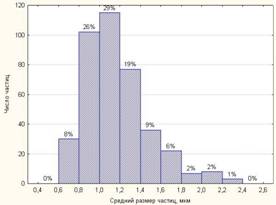
... поле – 2. Исследованиями установлено, что воздействие ультразвуковых колебаний на исходный порошок через жидкую среду приводит к его некоторому измельчению за счет разрушения агломератов. Сравнение микроструктуры керамики ЦТБС-3М, полученной различными методами, позволяет сделать вывод, что наименьшая пористость наблюдается у образцов, синтезированных из пресс-заготовок, полученных из порошка, ...
... переменного тока проводимости или тока смещения, где длина волны зависит от частоты колебания. Любой электрический ток, согласно электродинамике, всегда замкнут. Поэтому продольные электромагнитные волны всегда замкнуты независимо от того, представляют они переменный электрический ток проводимости или смещения. Продольные электрические возмущения поля имеют продольную ориентацию электрического ...
... потока Ф0 ...» Физические величины (справочник). 1991. С.1234. «Собственно говоря, постоянной Планка называется коэффициент пропорциональности ...» Квантовая физика. И.Е.Иродов. 2001. С.11. Электромагнитная волна де Бройля, как и фотон, представляет электромагнитный квант, состоящий из кванта электрического потока (заряда) и кванта магнитного потока. Длина волны де Бройля и энергия ...
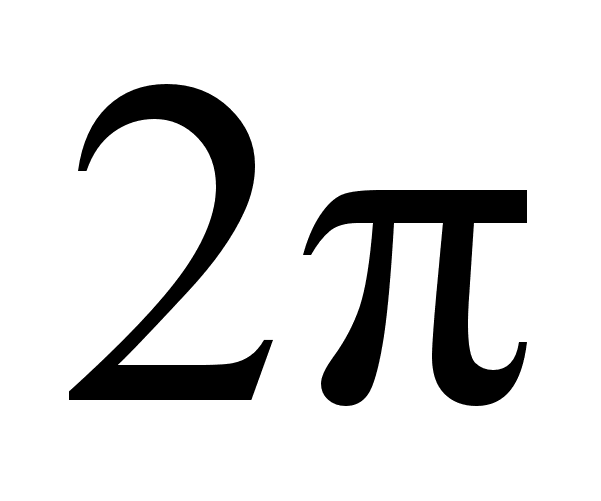
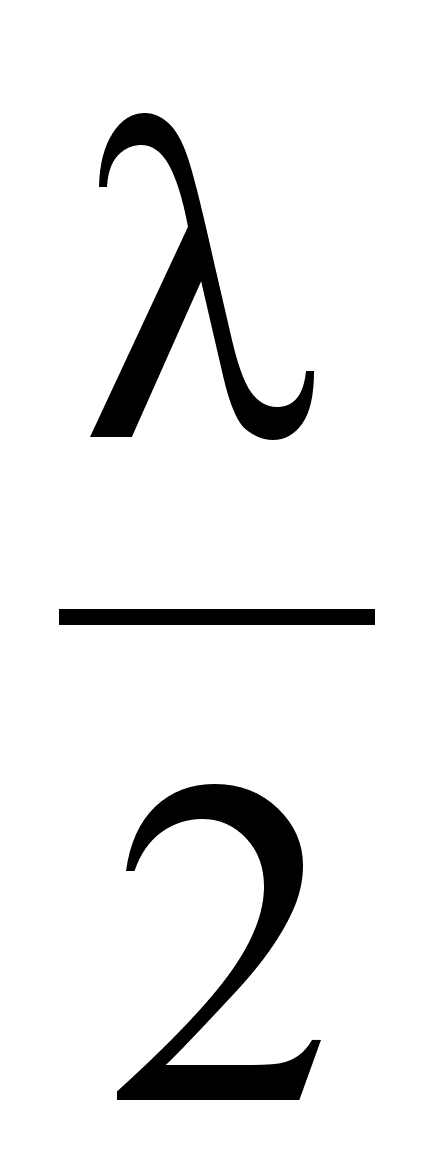
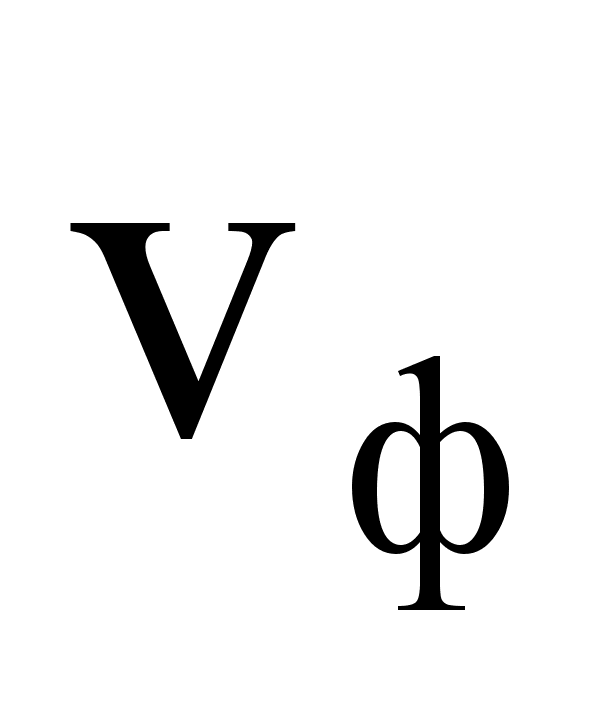


0 комментариев