Навигация
Плоские волны в реальных средах
38688
знаков
1
таблица
188
изображений
7.3. Плоские волны в реальных средах.
Предыдущий анализ относился к идеальным средам. В реальных средах часть энергии будет теряться в среде, значит амплитуда волны будет убывать. Любая реальная среда - набор связанных зарядов (диполей), могут быть и свободные заряды.
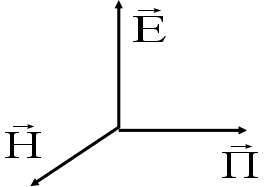
Часть энергии переходит в тепло. Количественно опишем процесс.
В реальных средах, при гармонических воздействиях проницаемости величины комплексные:
= `a - j a``
= a` - j a`` (7.3.1.)
Все рассуждения и результаты сохраняют силы, но параметры а а - комплексные.
Амплитудные соотношения.
С этой целью рассмотрим, что представляет собой волновое число в реальной среде:
____ _________________
k = aa = (a`- ja``)(a`- ja``) = - j (7.3.1.)
поскольку величины а и а - комплексные, то k - тоже величина комплексная. К каким последствиям это может привести ? Рассмотрим волновой процесс:
H (z,t) = y0 A e j(t-kz) = y0 A e t-(jz) =
= y0
A e
ej(t- (7.3.3.)
Параметр получил название коэффициента затухания. - фазовая постоянная - вещественная часть волнового числа.
Vф
=
/ в реальных
средах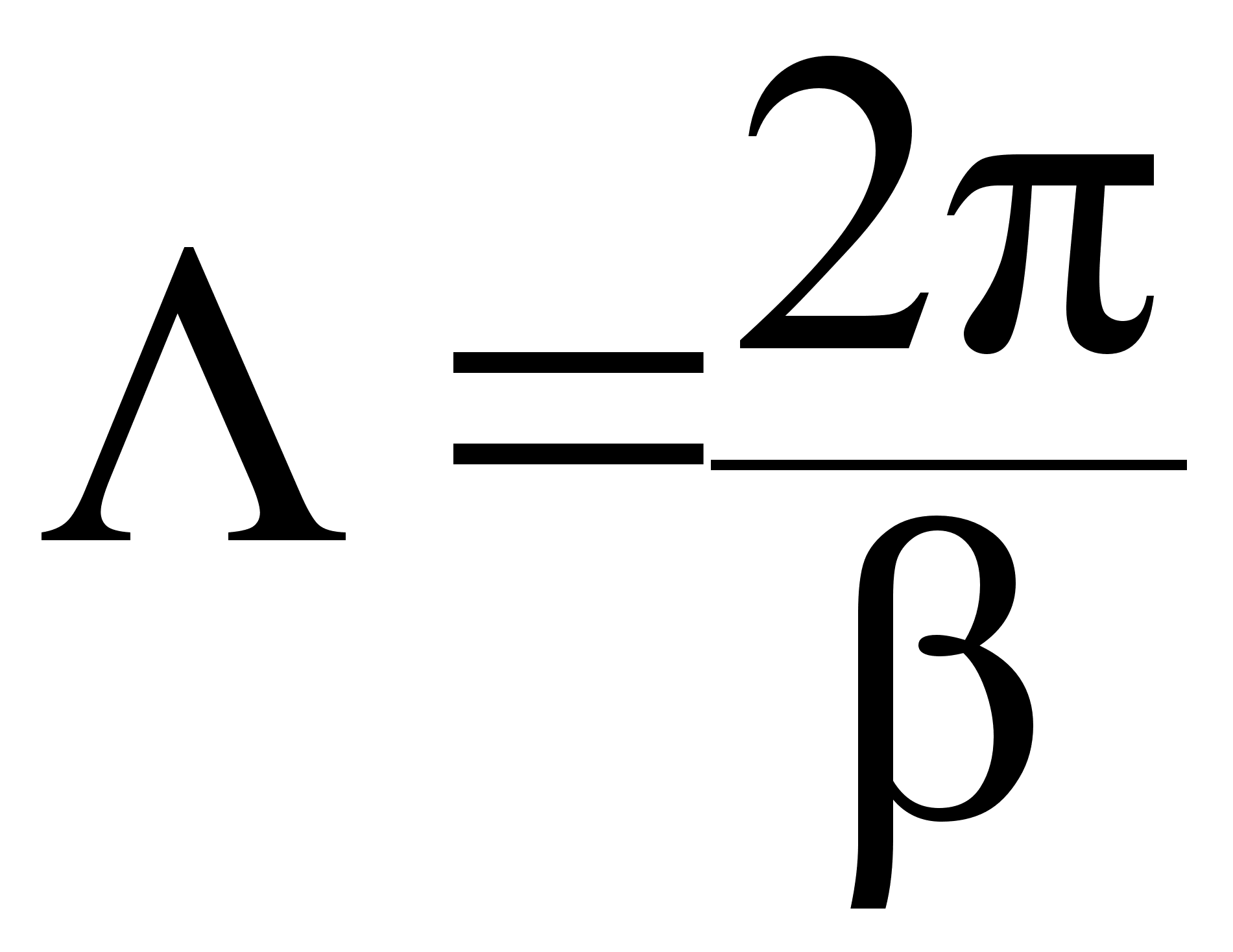 
(7.3.4.)
Понятие было введено для идеального диэлектрика. Если затухание мало, то можно выбрать точки, где поля отличаются по фазе на 2 и считать, что это . Если затухание очень велико, периодичность процесса теряет смысл (соленая вода), понятием можно пользоваться условно.
Количественная оценка.
Рассмотрим поведение амплитуды в точках:
в т. Z1 H(Z1) = A e - 1
в т. Z2 H(Z2) = A e - 2
Изменение
a
= 20 lg (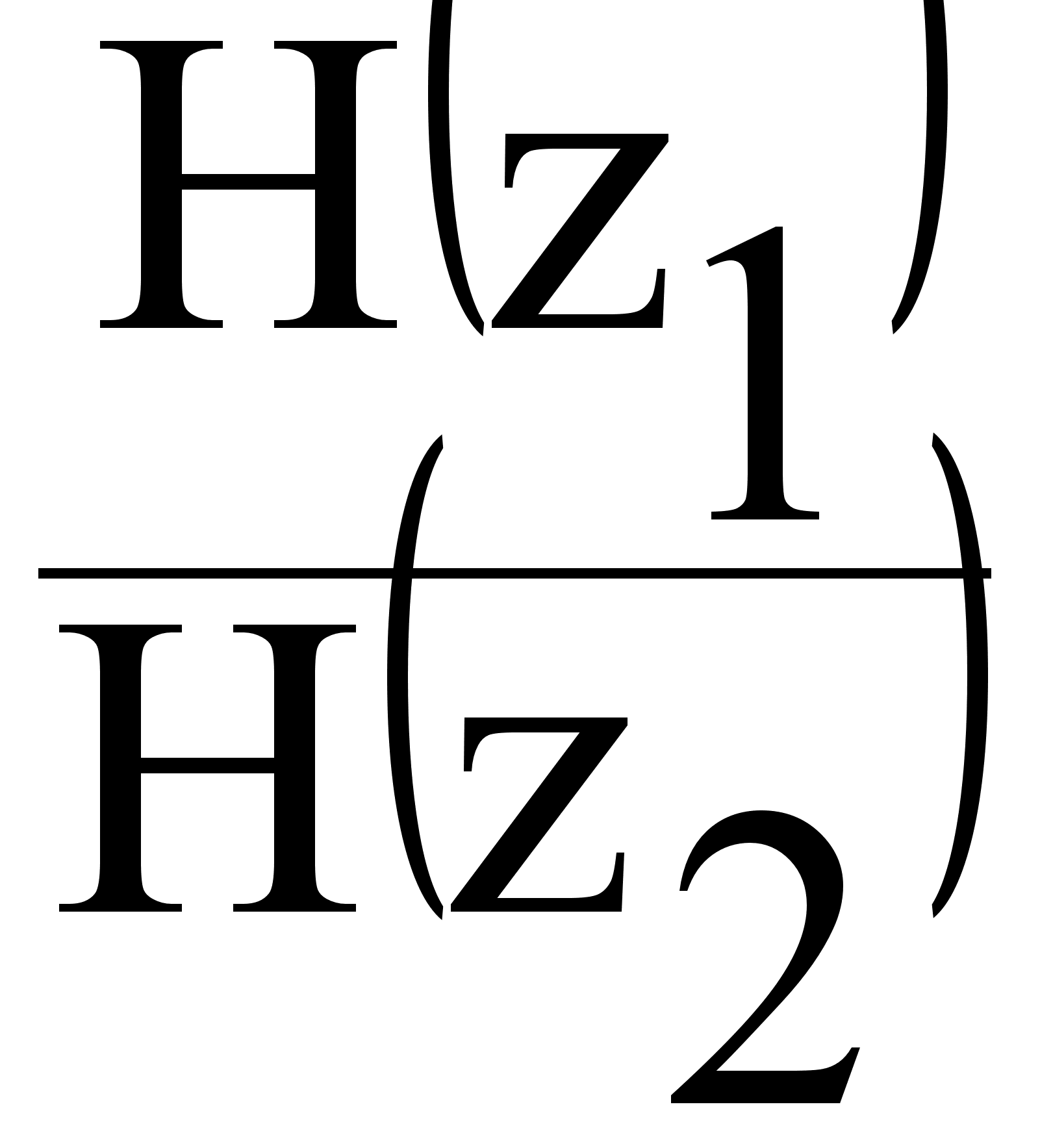
)
= 20 lg (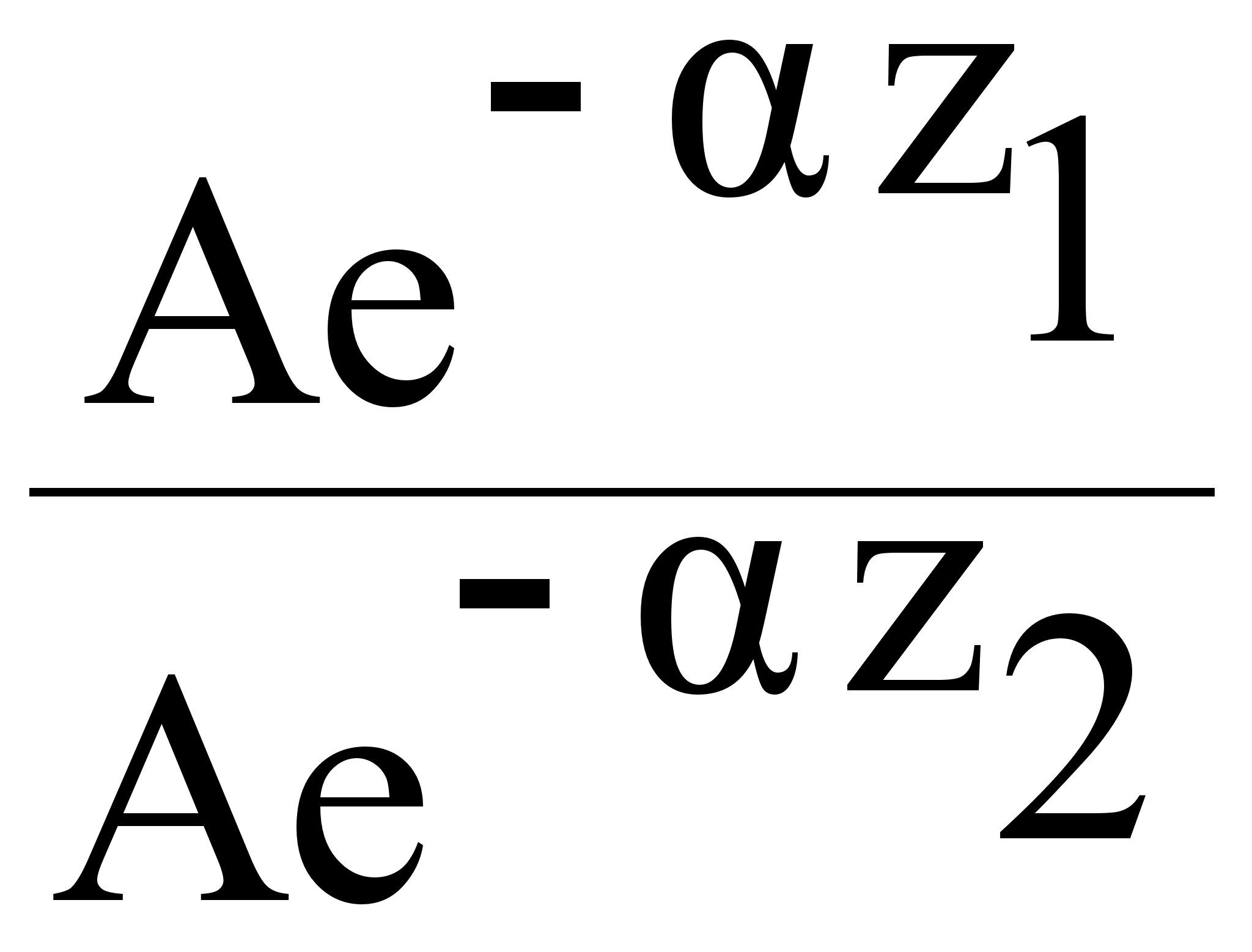
)
=
= 20 lg e 2- 1 = 20 (Z2 - Z1) lg ℓ
Z2 - Z1 = ℓ
a = 8,69 l [дБ] (7.3.5.)
во столько раз, пересчитанных в дБ уменьшилась амплитуда поля .
Под глубиной проникновения поля понимают расстояние, на котором амплитуда поля убывает в е раз
(вектор Е и Н).
Изменение поля Н = A e - . На расстоянии равном глубине проникновения в точке Z = 0, Н1 = А
в т. Z = 0 H2 = A e -
=
е = е - ;
0
= 1
0
= 
(7.3.6.)
Фазовые соотношения
Воспользуемся понятием “характеристическое сопротивление cреды”
____ ________________
Zc
=
= a`
- ja``/
a`-
ja``=Zc
ej (7.3.7.)
в реальных средах Zc величина комплексная. Поведение
Е и Н в реальной среде:
H(z,t) = y0 A e - e j(t-
E(z,t) = x0 A Zc e - e j(t- =
= x0 A Zce - e j(t- (7.3.8.)
Модуль характеристического сопротивления означает отношение амплитуд между электрическим и магнитным полями, а фаза характеристического сопротивления показывает величину сдвига фаз между
Е и Н. В реальных средах всегда Е и Н сдвинуты на некоторую величину.
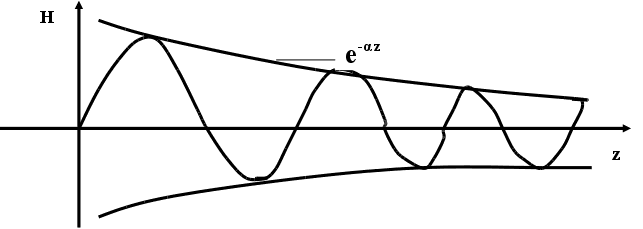
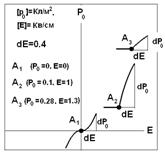
Волновой процесс в реальных средах
Расчет коэффициента затухания и
фазовой постоянной в реальной среде
Проведем расчет для частного случая, широко используемого на практике.
Реальная cреда не магнитный диэлектрик.
a = a`- ja`` ; a = a`- j0 = (7.3.9.)
(почва, вода)
Порядок расчета:
1) Из общих выражений для k:
____________
k = - j = (a`- ja``) a` (7.3.10.)
Выделим вещественную и мнимую часть. Для этого левую и правую часть возведем в квадрат, т.к. надо избавиться от радикалов:
2 - 2 j - 2 = 2a`a ` - j2a``a`
Два комплексных числа тогда равны, когда равны и вещественные и мнимые части.
2 - 2 = 2 a`a`
2 = 2 a``a`
2 a`a` = q - обозначим
2
a``a`
= 2
a`a
=
q tg
=
tg (7.3.11)
2
- 2
= q ;
= 
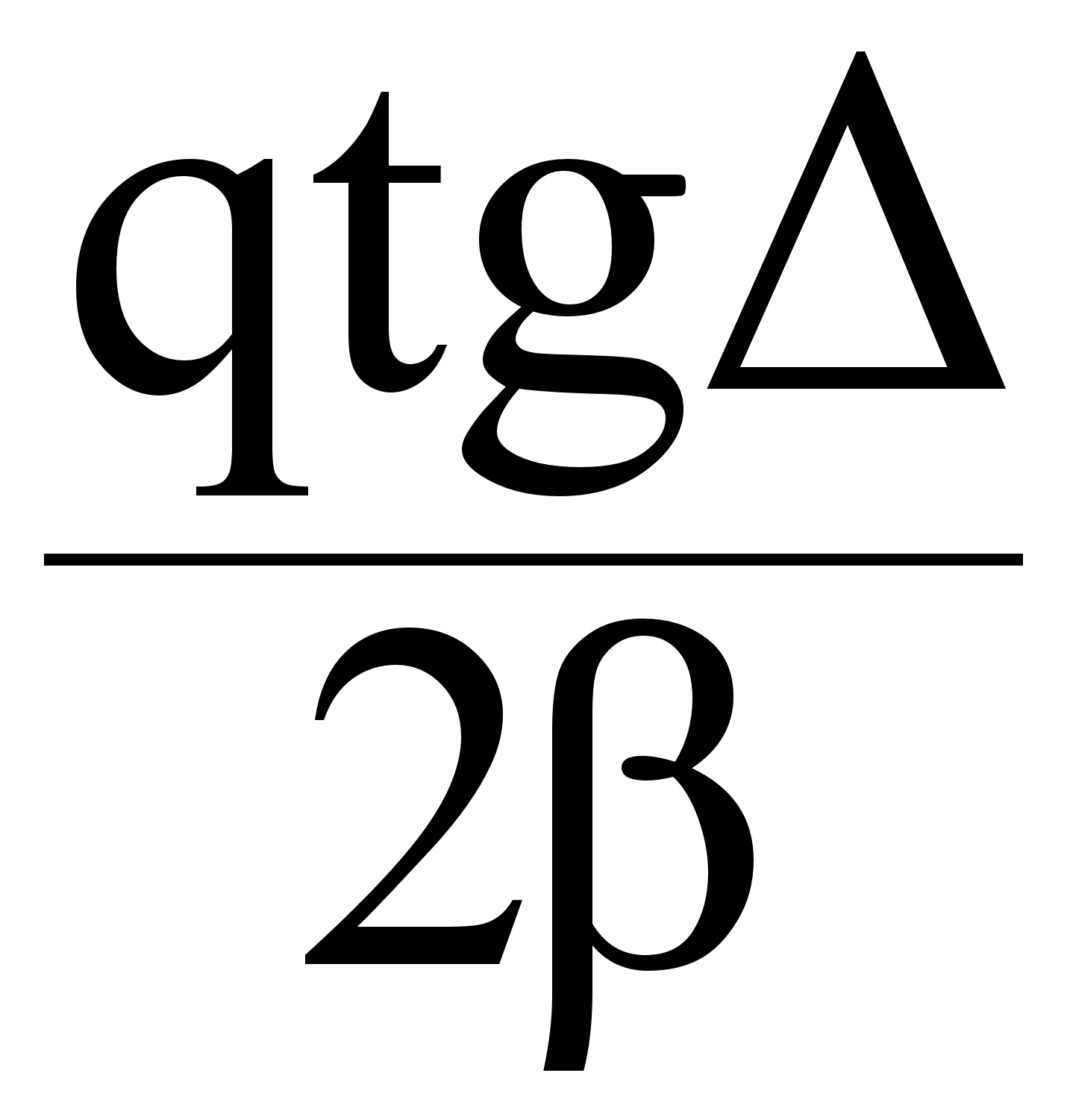
2 = q tg
2
- (
)
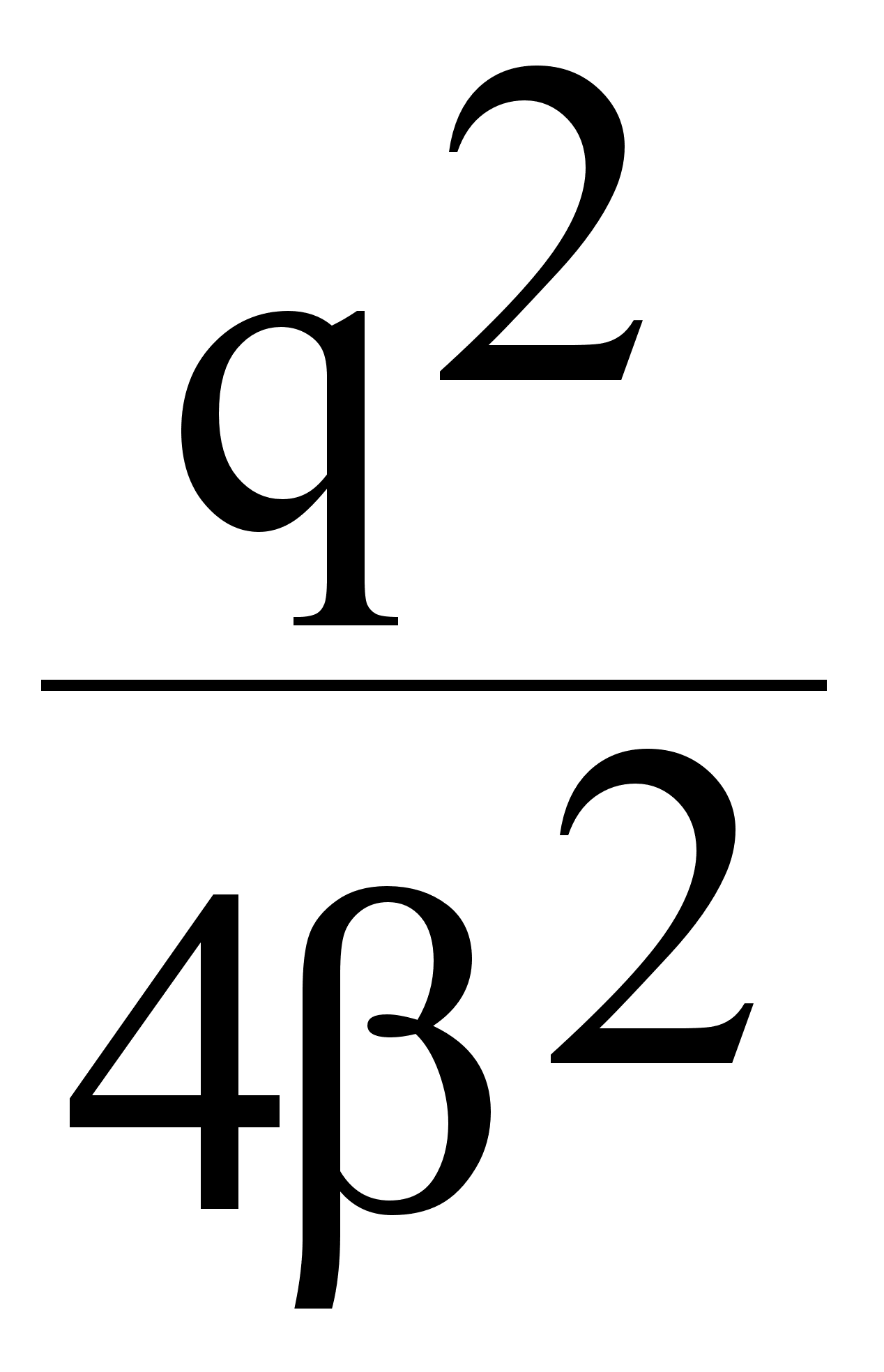tg2
- q = 0
4
- q2
- (
)
tg2
= 0
2
= 
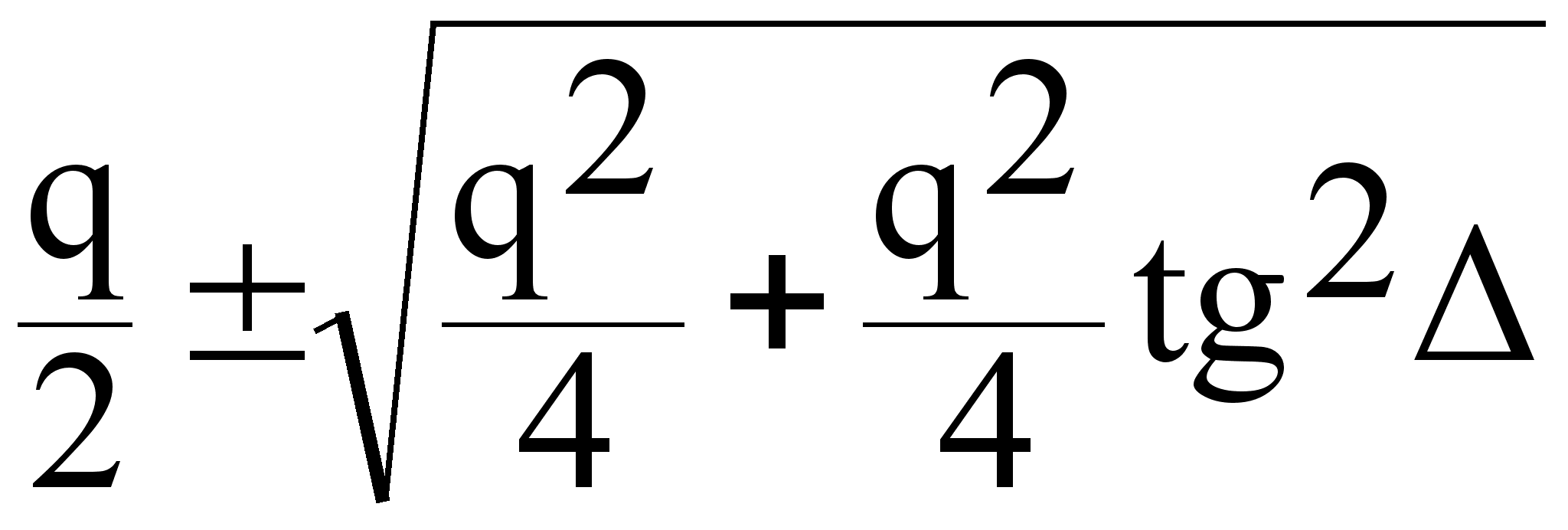
Какой знак взять + или - ?
Исходя из физического смысла оставляем только +, т.к. - будет отрицательная.
2 =
(1
+
1 + tg2)
=
(
1 + tg2 + 1) (7.3.12)
для решение аналогичное:
= 
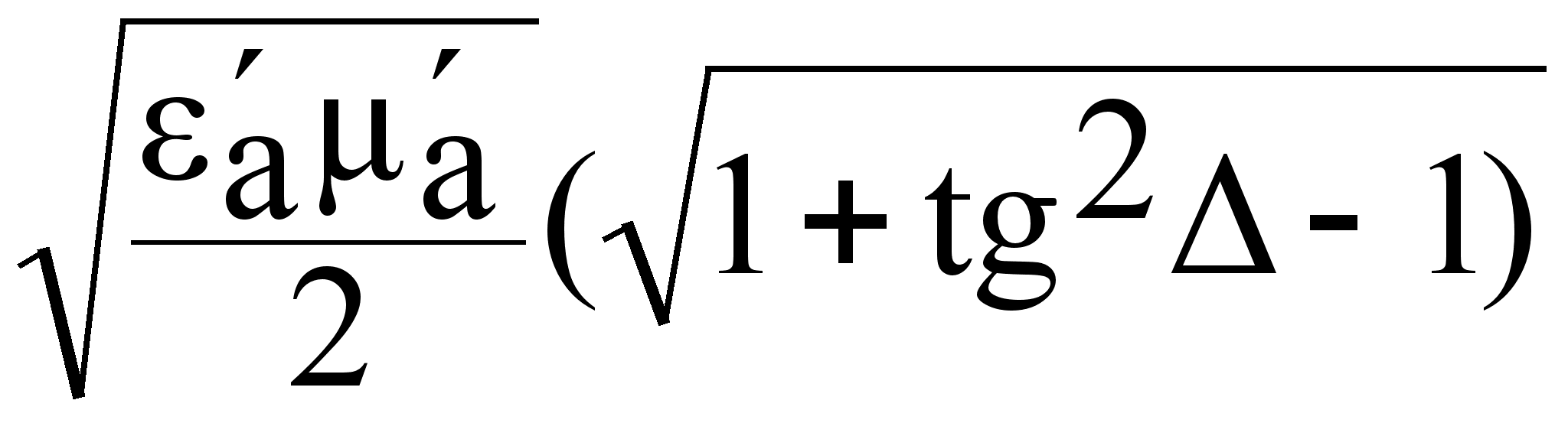(7.3.13)
Выводы:
1.
По определению Vф = 
Vф
= 
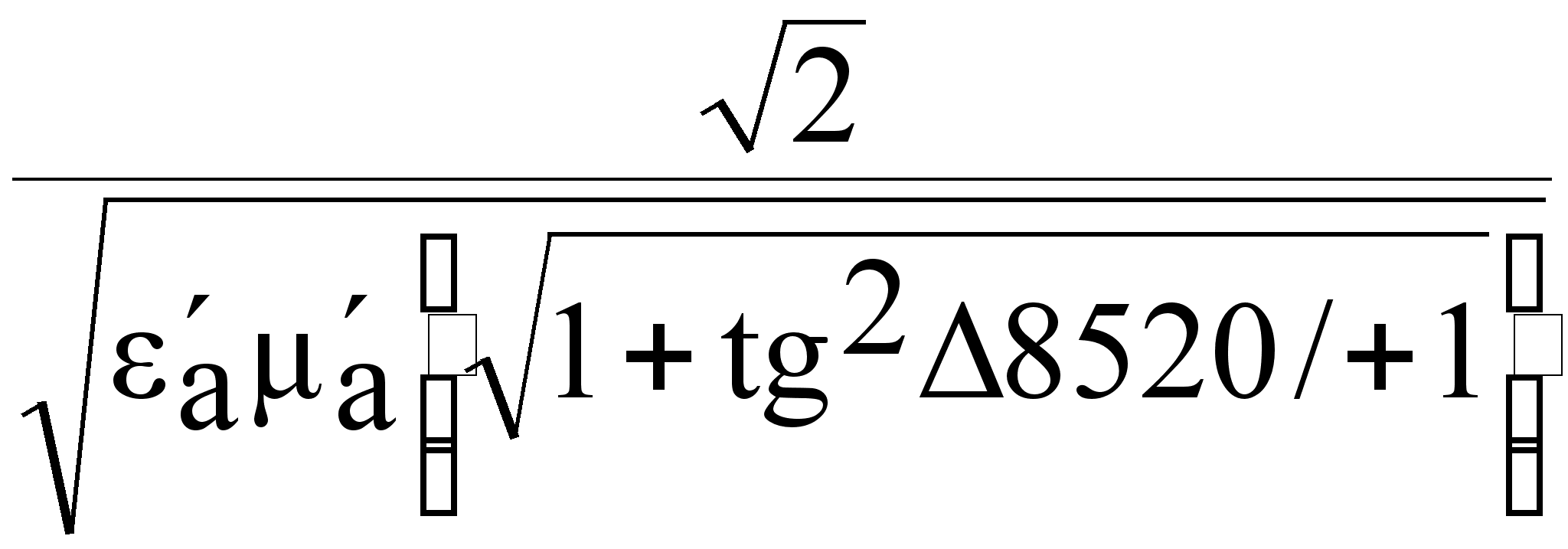
tg
= 
Vф зависит от частоты. Встретились с явлением дисперсии. Зависимость Vф от f называется дисперсией. Идеальная среда не обладает дисперсией.
= 0 - идеальная среда
0 - реальная
Рассмотрим поведение ЭМВ в двух случаях:
1) Среда с малыми потерями, малым затуханием:
tg tg , тем > . (7.3.15)
2) Среда с большими потерями.
tg >> 1
=
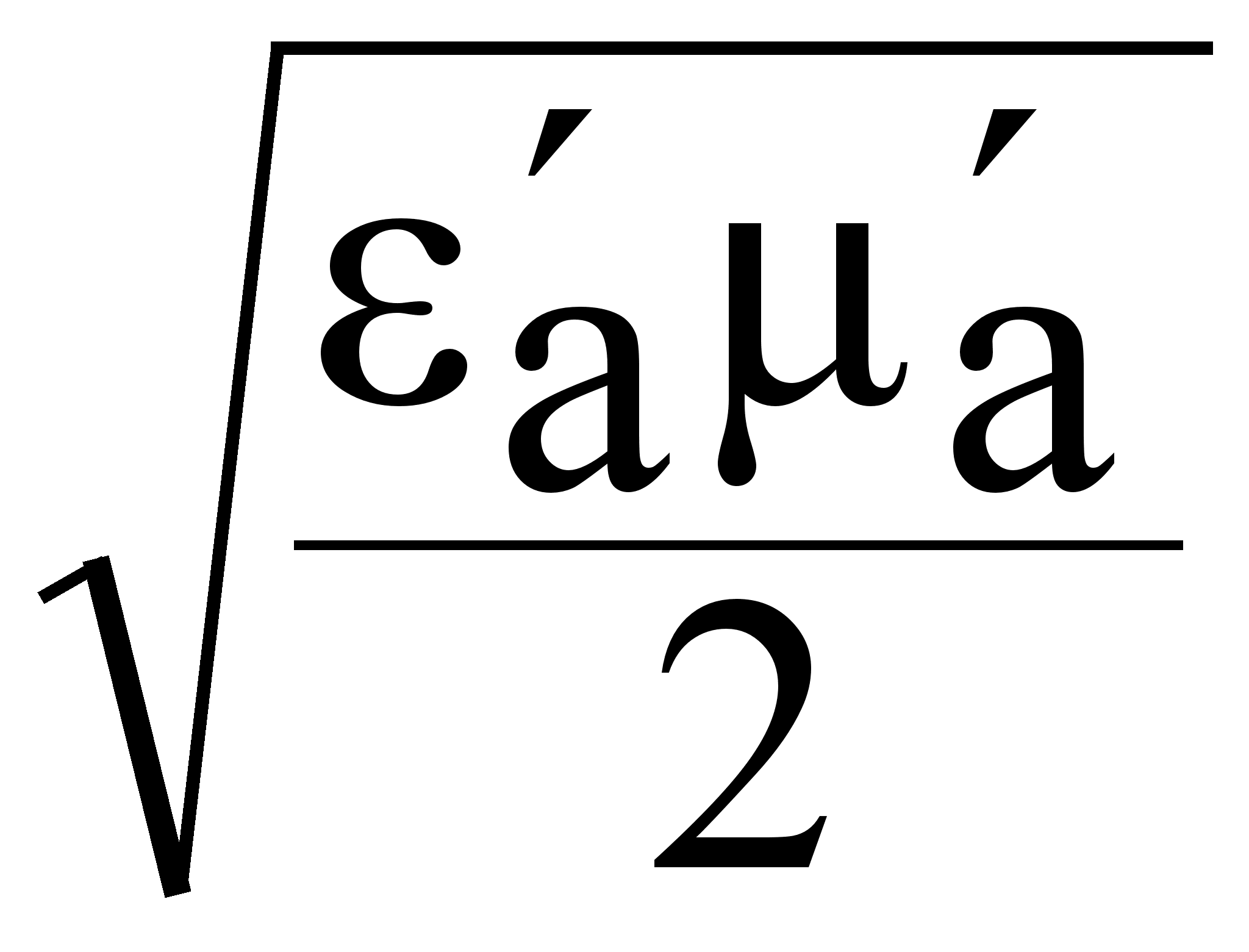tg
=
=
= 
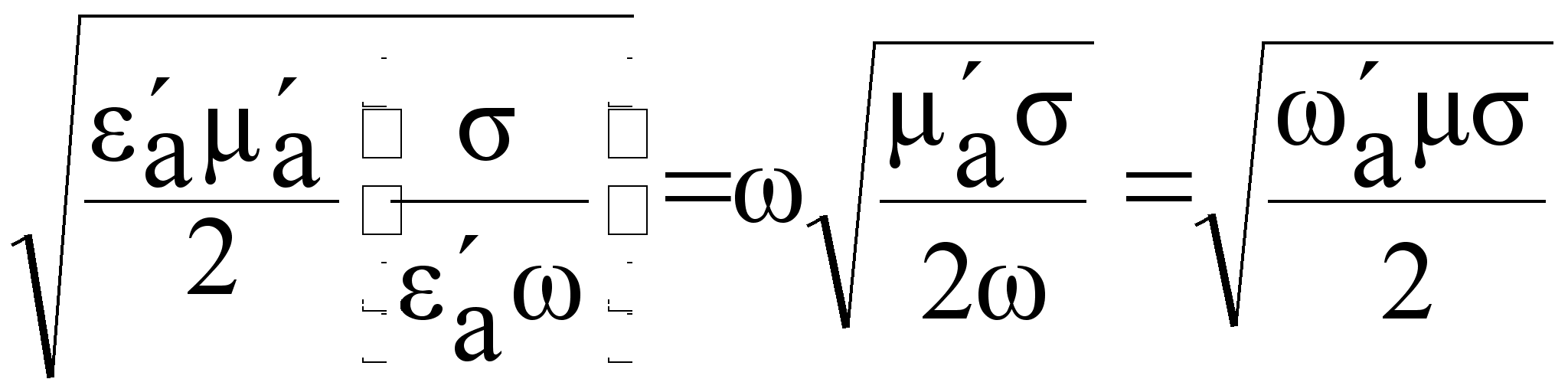
tg
= 
=
= 
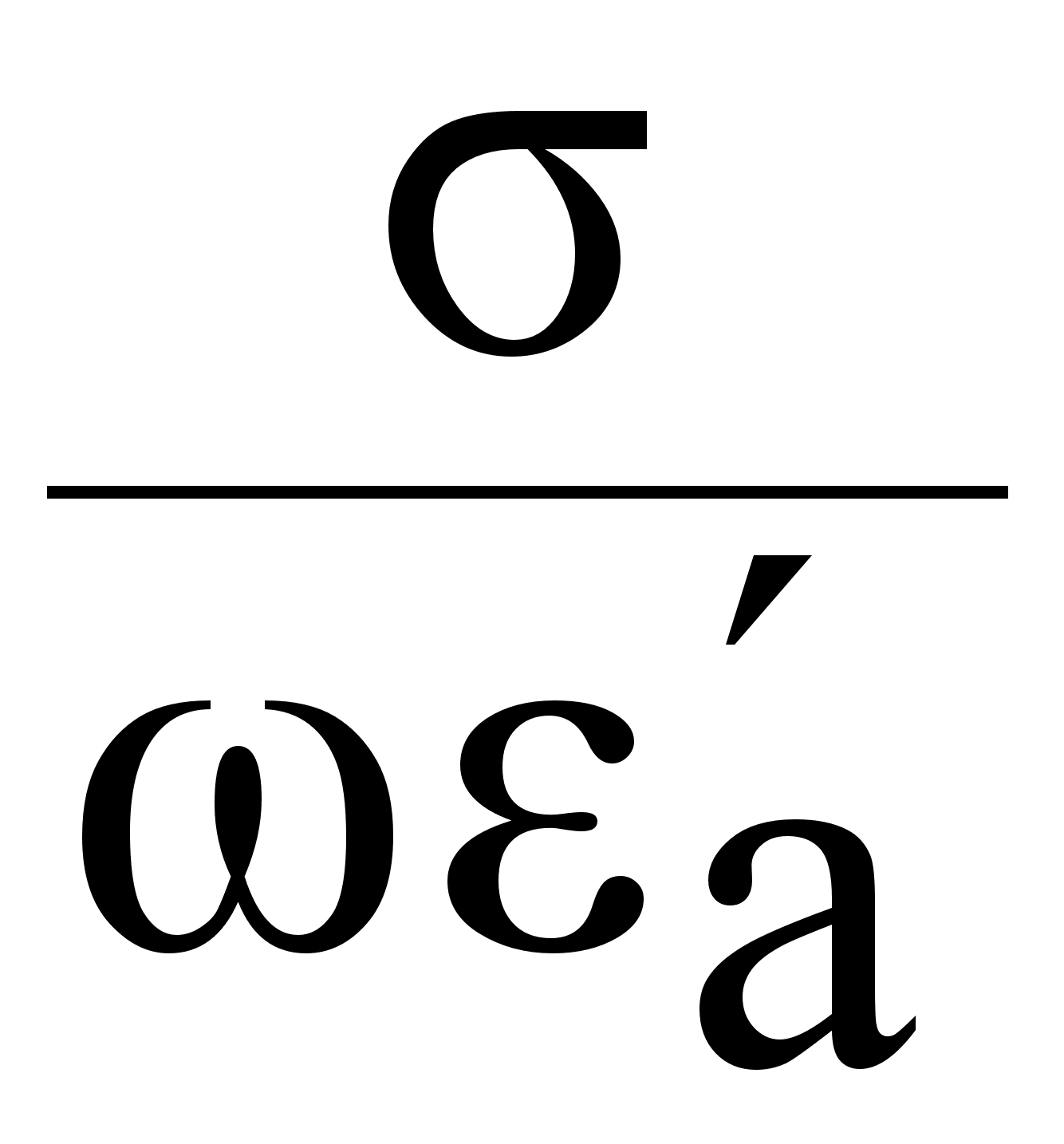
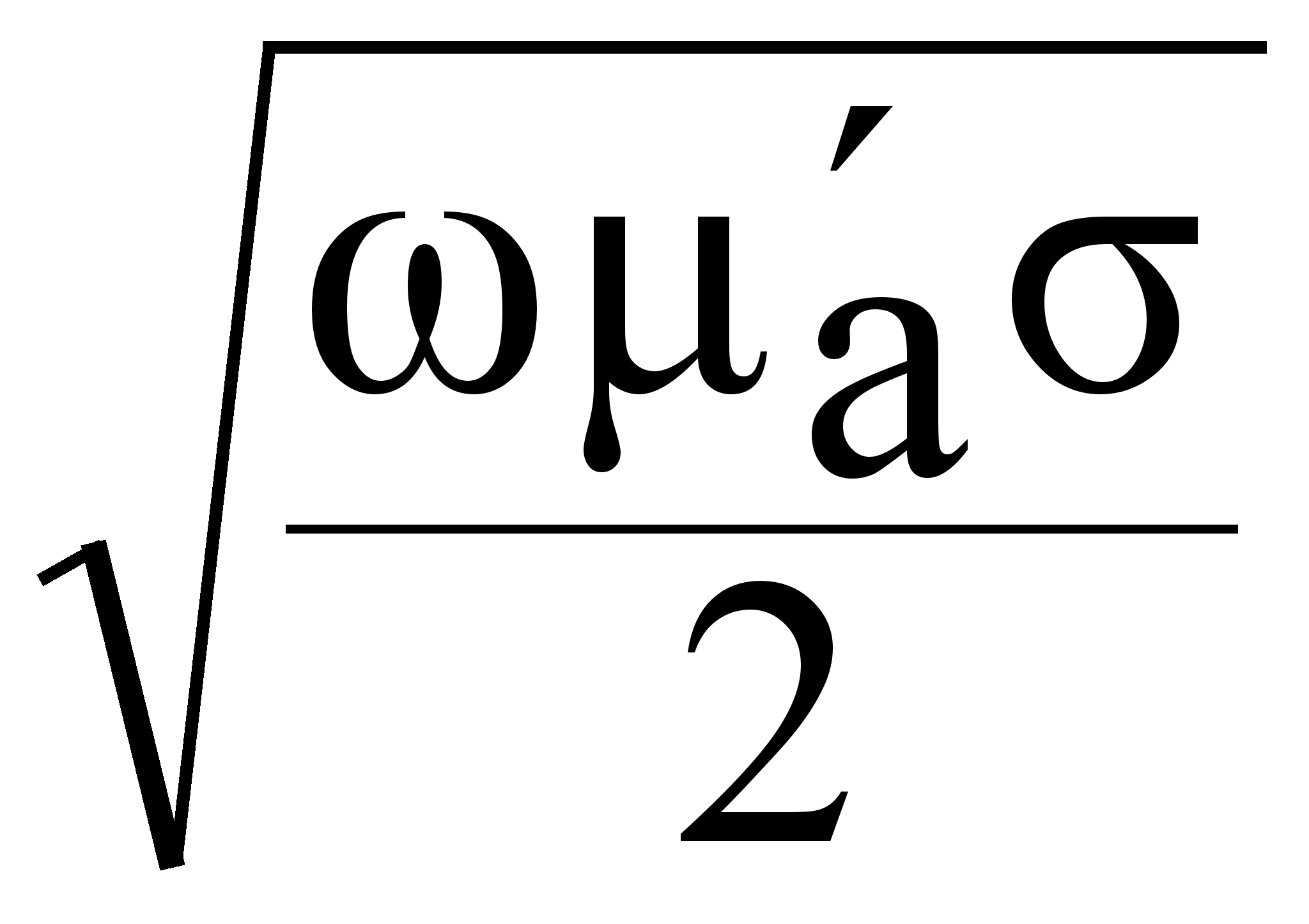(7.3.16.)
0
= 
Пример:
Определить во сколько раз уменьшается амплитуда волны на расстоянии равном длине волны (в среде с большими потерями).
e = e = e = e = 540 раз
Похожие работы
... в пространстве. Утверждение о существовании электромагнитных волн является непосредственным следствием решения системы уравнений Максвелла. Согласно этой теории следует, что переменное электромагнитное поле распространяется в пространстве в виде волн, фазовая скорость которых равна: где - скорость света в вакууме, , - электрическая и магнитная постоянные, , - соответственно диэлектрическая ...
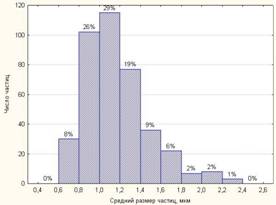
... поле – 2. Исследованиями установлено, что воздействие ультразвуковых колебаний на исходный порошок через жидкую среду приводит к его некоторому измельчению за счет разрушения агломератов. Сравнение микроструктуры керамики ЦТБС-3М, полученной различными методами, позволяет сделать вывод, что наименьшая пористость наблюдается у образцов, синтезированных из пресс-заготовок, полученных из порошка, ...
... переменного тока проводимости или тока смещения, где длина волны зависит от частоты колебания. Любой электрический ток, согласно электродинамике, всегда замкнут. Поэтому продольные электромагнитные волны всегда замкнуты независимо от того, представляют они переменный электрический ток проводимости или смещения. Продольные электрические возмущения поля имеют продольную ориентацию электрического ...
... потока Ф0 ...» Физические величины (справочник). 1991. С.1234. «Собственно говоря, постоянной Планка называется коэффициент пропорциональности ...» Квантовая физика. И.Е.Иродов. 2001. С.11. Электромагнитная волна де Бройля, как и фотон, представляет электромагнитный квант, состоящий из кванта электрического потока (заряда) и кванта магнитного потока. Длина волны де Бройля и энергия ...
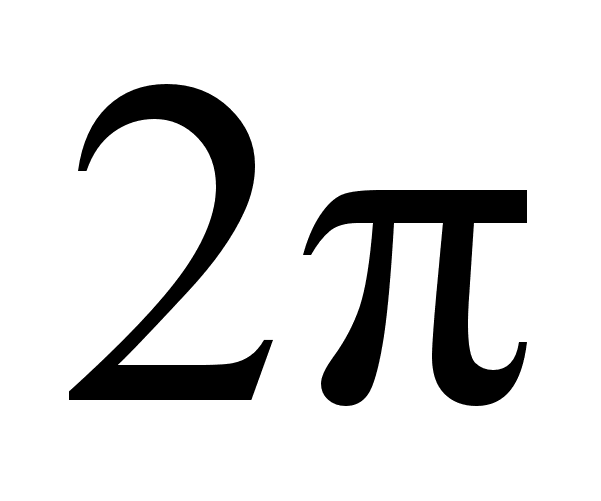
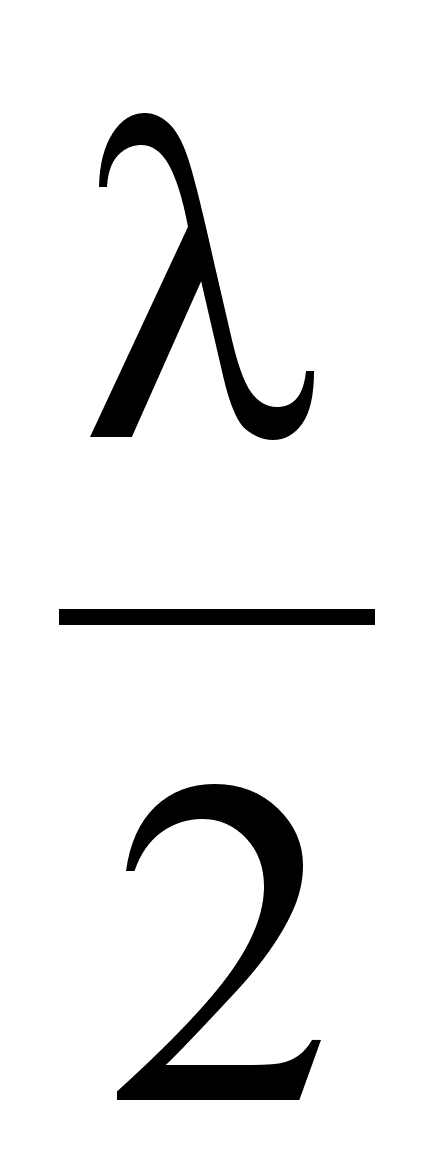
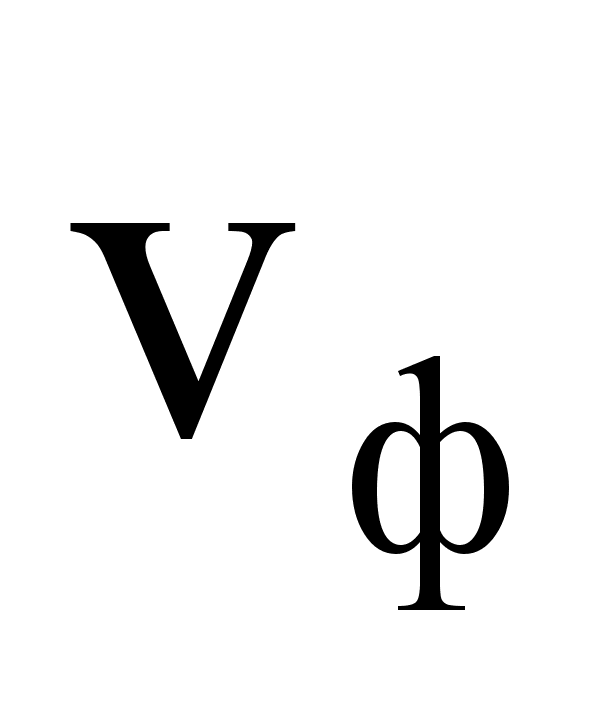
0 комментариев