Основные свойства реальных жидкостей
Два подхода к описанию движения сплошной среды
Уравнение неразрывности
Гидростатика
Потенциальное движение
Закон Паскаля
Сила давления жидкости на плоскую стенку
Анализ уравнения Бернулли
Измерение скорости
Два режима течения жидкости
Определение потерь напора на трение по длине
Гидравлический расчет напорных трубопроводов
Из формулы ... видно, что увеличение давления пропор-
Источник и сток
Тензор плотности потока импульса для вязких течений
Навигация
Потенциальное движение
Лекции по физике
118786
знаков
4
таблицы
0
изображений
2. Потенциальное движение
Движение жидкости, при котором во всём пространстве
...
называется потенциальным (или безвихревым) в противоположность вихревому движению, при котором ротор скорости отличен от нуля.
Таким образом, мы пришли бы к выводу, что стационарное обтекание взятого тела натекающим из бесконечности однородным потоком
должно быть потенциальным. Поскольку на бесконечности натекающий
поток однороден, его скорость ... , так что ... = 0 на всех
линиях тока.
Однако, ввиду наличия стенки нельзя провести в жидкости замкнутый контур, который охватывал бы такую линию тока.
...
...
В результате возникает картина течения, характеризующаяся наличием отходящей от тела "поверхности тангенциального разрыва", на которой скорость жидкости терпит разрыв непрерывности.
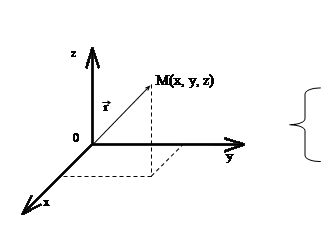
Как и всякое векторное поле с равным нулю ротором, скорость потенциально движущейся жидкости может быть выражена в виде градиента от некоторого скаляра, называемого потенциалом скорости ...
...
Напишем уравнения Эйлера в виде
...
и подставив в него ........, получаем
...
Откуда находим следующе равенство
...
где ... произвольная функция времени. Это равенство представляет собой первый интеграл уравнений потенциального движения.
При стационарном движении имеем ... = 0, ......... и интеграл переходит в уравнение Бернулли
...
Отметим существенные отличия между уравнениями Бернулли в случае потенциального и непотенциального движения. ..... в правой части этого уравнения есть величина, постоянная вдоль каждой линии тока, но вообще говоря, различная для разных линий тока.
При потенциальном же движении ... в уравнении Бернулли есть величина, постоянная во всём объёме жидкости.
3. Несжимаемые жидкости
Для плоских течений жидкостей их плотность можно считать постоянной вдоль всего объёма жидкости в течение всего времени движения. Такое движение называется движением несжимаемой жидкости.
Общие уравнения гидродинамики для несжимаемой жидкости упрощаются. Уравнение неразрывности при ......... принимает простой вид
...
уравнения Эйлера не меняют своего вида, запишем их в виде
...
Для несжимаемой жидкости тепловая функция записывается следующим образом
...
Тогда уравнение Бернулли для несжимаемой жидкости имеет вид
...
Особенно упрощается уравнение для потенциального течения несжимаемой жидкости.
При подстановке ........ в уравнение неразрывности ..... = 0, получим
...
то есть уравнение Лапласа для потенциала ... .
Граничные условия. К этому уравнению должны быть добавлены граничные условия на поверхности соприкосновения жидкости с твёрдыми телами:
- на неподвижных твёрдых поверхностях нормальная к поверхности компонента ... скорости жидкости должна быть равна нулю, для движущихся тел ... должна быть равна проекции скорости движения тела на направление той же нормали.
С другой стороны, скорость ... равна производной от потенциала ... по направлению нормали
...
Таким образом, граничные условия гласят в общем случае, что .... является на границах заданной функцией координат и времени.
При потенциальном движении скорость связана с давлением для несжимаемой жидкости соотношением
...
Если движение жидкости является потенциальным и вызвано движением некоторого тела то уравнение Лапласа не содержит явно времени, время входит в решение через граничные условия.
Из уравнения Бернулли ..................... видно, что при стационарном движении несжимаемой жидкости вне поля тяжести наибольшее значение давления достигается в точках, где скорость обращается в нуль. Такая точка обычно имеется на поверхности обтекаемого жидкостью тела (точка О) и называется критической точкой. Если ... - скорость набегающего на тело потока жидкости (скорость на бесконечности), а ... - давление в критической точке равно
...
Если распределение скоростей в движущейся жидкости зависит только от двух координат, то о таком течении говорят как о двумерном или плоском. Для решения задач о двумерном течении несжимаемой жидкости иногда удобнее использовать функцию тока. Из уравнения неразрывности
...
видно, что компоненты скорости могут быть записаны в виде производных
...
от некоторой функции ... , называемой функцией тока. Уравнение неразрывности при этом удовлетворяется автоматически.
...
Зная функцию тока, можно непосредственно определить форму линий тока для стационарного движения жидкости. Дифференциальное уравнение линий тока
...
или
...
оно выражает условие параллельности касательной к линии тока и направления вектора скорости.
Подставляя сюда выражение для скоростей через функцию тока
...
откуда ........ Таким образом, линии тока представ-
ляют собой семейство кривых, получающихся приравниванием функции
тока ... постоянной.
Если между точками 1 и 2 в плоскости .... провести кривую,
то поток жидкости ... через эту кривую определится разностью значений функции тока в этих точках независимо от формы кривой.
Действительно, если ... - проекция скорости на нормаль к кривой в данной точке, то
...
или
...
Мощные методы решения задач о простом потенциальном обтекании несжимаемой жидкостью различных профилей связаны с применением к ним теории функций комплексной переменной.
Тема 6
ГИДРОСТАТИКА
1. Силы, действующие на жидкость. Давление.
Единицы измерения давления.
2. Закон Паскаля.
3. Дифференциальное уравнение равновесия жидкости.
4. Виды давления ( барометрическое, абсолютное, избыточное, манометрическое ).
5. Приборы для измерения давления.
6. Сила давления жидкости на плоскую стенку.
7. Простейшие гидравлические машины.
8. Закон Архимеда.
9. Равновесие и остойчивость тел, полностью погруженных в жидкость.
1. Силы, действующие на жидкость. Давление.
Единицы измерения давления
Рассечем жидкость, находящуюся в объеме ... (например, сосуде) некоторой поверхностью на две части I и II.
Рассмотрим жидкость в объеме I. Все, что окружает этот объем, отбросим (дно, боковые стенки и т.д.) и действие отброшенного заменим соответствующими силами. Эти силы называются поверхностными.
Кроме них на жидкость действуют еще массовые силы (силы тяжести и инерции), которые пропорциональны массе тела.
Выделим из жидкости некоторый объем. Возьмем на поверхности этого объема бесконечно малую площадку ... . Hа эту площадку действует поверхностная сила ... . Разложим эту силу на нормальную ... и касательную ...
Hормальная сила, приходящаяся на единицу площади, называется давлением и обозначается буквой ... , т.е.
...
Измеряется давление в ....
Сила трения (касательная сила), приходящаяся на единицу площади, обозначается буквой ..., т.е.
...
Сила трения обычно пропорциональна градиенту скорости ... . Для жидкости, находящейся в равновесии (в покое), сила трения равна нулю, так как в этом случае ... .
Похожие работы
... свойства. А.у.т. - тело, для которого силы однозначно определяют деформации и наоборот. Правильность выбранной абстракции подтверждается совпадением, определенной точностью результатов теории и опыта. Физика - наука, устанавливающая закономерные связи посредством наблюдений явлений в природе и посредством лабораторных опытов. Согласие результатов научного анализа с результатами опыта - критерий ...
... так, как большинство материалов относится к устному творчеству, откуда и были получены, также есть выдержки из книг: «Физики шутят», «Физики продолжают шутить», «Сборник задач по физике» Г. Остера. Шутки, которые шутят физики. Один математик спросил коллегу, известного своими религиозными убеждениями: - Вы, что же, верите в единого ...
... фара́да). 1 фарад равен электрической ёмкости конденсатора, при которой заряд 1 кулон создаёт между обкладками конденсатора напряжение 1 вольт. Ф = Кл/В = A·c/B Единица названа в честь английского физика Майкла Фарадея Фарад — очень большая ёмкость. Емкостью 1Ф обладал бы уединенный шар, радиус которого был бы равен 13 радиусам Солнца. Для сравнения, ёмкость Земли (шара размером с ...
... гальванометра отклонялась (то же происходило и при поднятии электромагнита из катушки). Эта схема напоминает рисунок из лабораторного журнала Фарадея. Удивительно, как схожи оказались эксперименты двух великих физиков, работавших независимо друг от друга на разных континентах! В своей статье, написанной уже после знакомства с опытом Фарадея, Генри, отдавая должное английскому физику, подчеркнул, ...
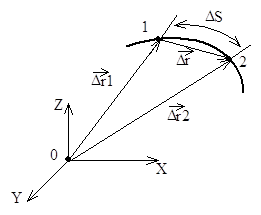
0 комментариев