Навигация
![]() при
при ![]() →
→![]() 0,
0,
если ![]() при
при ![]() →
→![]() 0.
0.
Степенные ряды – это специальный случай рядов в нормированном пространстве, когда члены ряда зависят от параметра![]() .
.
Рассмотрим в нормированном пространстве X ряд вида ![]() , где xк Î X, а
, где xк Î X, а ![]() – вещественное или комплексное переменное. Поскольку можно ввести новую переменную
– вещественное или комплексное переменное. Поскольку можно ввести новую переменную ![]() –
–![]() 0 =
0 = ![]() , то в дальнейшем мы полагаем
, то в дальнейшем мы полагаем ![]() 0 = 0 и рассматриваем степенные ряды вида
0 = 0 и рассматриваем степенные ряды вида
![]() (1)
(1)
Конечная сумма ![]() называется частичной суммой степенного ряда (1).
называется частичной суммой степенного ряда (1).
Пусть ![]() – множество всех точек
– множество всех точек ![]() , для которых ряд (1) сходится.
, для которых ряд (1) сходится. ![]() называется областью сходимости ряда (1).
называется областью сходимости ряда (1).
Сумму ряда (1) при ![]() Î
Î ![]() обозначим через S(
обозначим через S(![]() ) (это абстрактная функция, определенная на
) (это абстрактная функция, определенная на ![]() со значениями в X), при этом будем писать
со значениями в X), при этом будем писать
![]()
![]() , при
, при ![]() Î
Î ![]() .
.
Последнее равенство означает, что Sn(![]() ) → S(
) → S(![]() ) при n→∞ для всех
) при n→∞ для всех ![]() Î
Î ![]() .
.
Очевидно, область сходимости любого степенного ряда (1) не пуста, так как 0 Î ![]() . Как и в случае скалярных функций, справедлива следующая теорема.
. Как и в случае скалярных функций, справедлива следующая теорема.
Теорема 10 (Абель). Пусть![]() 0 ≠ 0 и
0 ≠ 0 и ![]() 0 Î
0 Î ![]() , тогда круг
, тогда круг ![]() содержится в
содержится в ![]() . Во всяком круге Sr(0), где r <
. Во всяком круге Sr(0), где r < ![]() , ряд (1) сходиться абсолютно и равномерно относительно
, ряд (1) сходиться абсолютно и равномерно относительно ![]() .
.
Теорема 11. Пусть два степенных ряда равны в круге SR(0), R>0:
![]()
![]() ;
;
тогда равны все их коэффициенты: ![]() (k=0, 1, 2, …)
(k=0, 1, 2, …)
Дифференцирование абстрактных функций
Пусть функция ![]() числового переменного λ со значениями в банаховом пространстве X определена в окрестности точки λ0.
числового переменного λ со значениями в банаховом пространстве X определена в окрестности точки λ0.
По определению производной x’(λ0) функции x(λ) в точке λ0 называется предел
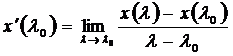 ,
,
если этот предел существует (и конечен). Если ![]() имеет производную в точке λ0, то она называется дифференцируемой в этой точке.
имеет производную в точке λ0, то она называется дифференцируемой в этой точке.
§5. Аналитические абстрактные функции и ряды Тейлора
Абстрактную функцию x(![]() ) будем называть аналитической при
) будем называть аналитической при ![]() =0, если она представима в некоторой окрестности точки
=0, если она представима в некоторой окрестности точки ![]() =0 сходящимся степенным рядом:
=0 сходящимся степенным рядом:
![]() (1)
(1)
с ненулевым радиусом сходимости.
Теорема 12. Если x(![]() ) – аналитическая абстрактная функция при
) – аналитическая абстрактная функция при ![]() =0, то x(
=0, то x(![]() ) непрерывна в круге SR(0), где R – радиус сходимости степенного разложения (1).
) непрерывна в круге SR(0), где R – радиус сходимости степенного разложения (1).
Теорема 13. Если x(![]() ) – аналитическая абстрактная функция при
) – аналитическая абстрактная функция при ![]() =0, то x(
=0, то x(![]() ) дифференцируема в круге SR(0) сходимости своего степенного разложения.
) дифференцируема в круге SR(0) сходимости своего степенного разложения.
Пусть x(![]() ) бесконечно дифференцируема в точке 0. Ряд вида
) бесконечно дифференцируема в точке 0. Ряд вида
![]()
называется рядом Тейлора функции x(![]() ).
).
Если x(![]() ) аналитична при
) аналитична при ![]() =0, то ее ряд Тейлора, в силу теоремы 10, является ее степенным разложением и, значит, сходится к ней в SR(0).
=0, то ее ряд Тейлора, в силу теоремы 10, является ее степенным разложением и, значит, сходится к ней в SR(0).
Понятие абстрактной аналитической функции используется в широко применяемом на практике методе малого параметра.
§6. Метод малого параметра в простейшем случае
Рассмотрим следующее уравнение:
Аx –![]() Сx=y. (1)
Сx=y. (1)
Здесь А, С Î L(X,Y) и y Î Y заданы, ![]() - скалярный параметр,
- скалярный параметр, ![]() , а неизвестное x разыскивается в X. Если
, а неизвестное x разыскивается в X. Если ![]() , т.е.
, т.е.
![]() , (2)
, (2)
то, согласно теореме 9, оператор А–![]() С непрерывно обратим, и тогда решение уравнения (1) существует, единственно и задается явной формулой
С непрерывно обратим, и тогда решение уравнения (1) существует, единственно и задается явной формулой
![]() . (3)
. (3)
Отсюда видно, что в круге (2) решение является аналитической функцией параметра ![]() и, следовательно, может быть найдено в виде
и, следовательно, может быть найдено в виде
![]() (4)
(4)
На этой идее основывается метод малого параметра для уравнения (1). Подставим ряд (4) в уравнение (1) и, согласно теореме единственности разложения в степенной ряд, приравниваем коэффициенты при одинаковых степенях ![]() в правой и левой частях получившегося тождества:
в правой и левой частях получившегося тождества:
![]() .
.
Таким образом, мы приходим к следующей рекуррентной системе уравнений для определения x0, x1, …:
Аx0=y, Аx1=Сx0, …, Аxк=Сxк-1, …
Так как А непрерывно обратим, то отсюда последовательно находим
x0=А–1y, x1= А–1(СА–1)y, …, xк= А–1(СА–1)кy, …
Следовательно,
![]() . (5)
. (5)
Мы получили решение (3), разложенное в степенной ряд. Если мы хотим оборвать степенной ряд и ограничиться приближенным решением
![]()
то можно оценить ошибку. Вычитая из ряда (5) его частичную сумму (6) и оценивая разность по норме, получим
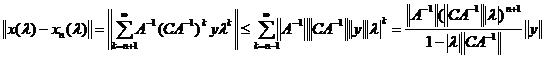 .
.
§7. Метод малого параметра в общем случае
Пусть дано уравнение
А(![]() )х = у(
)х = у(![]() ). (1)
). (1)
Здесь А(![]() )Î L(X,Y) задана при каждом
)Î L(X,Y) задана при каждом ![]() ,
, ![]() , или, как говорят, А(
, или, как говорят, А(![]() ) – оператор-функция. Пусть А(
) – оператор-функция. Пусть А(![]() ) аналитична при
) аналитична при ![]() =0, а оператор А(0) непрерывно обратим, у(
=0, а оператор А(0) непрерывно обратим, у(![]() ) – заданная аналитическая функция
) – заданная аналитическая функция ![]() при
при ![]() =0 со значениями в Y. Неизвестное x разыскивается в X.
=0 со значениями в Y. Неизвестное x разыскивается в X.
Аналитичность А(![]() ) и у(
) и у(![]() ) в точке 0 означает, что они разлагаются в следующие степенные ряды с ненулевыми радиусами сходимости, которые равны
) в точке 0 означает, что они разлагаются в следующие степенные ряды с ненулевыми радиусами сходимости, которые равны ![]() и
и ![]() соответственно:
соответственно:
![]() ,
, ![]() . (2)
. (2)
Из аналитичности А(![]() ) следует непрерывность А(
) следует непрерывность А(![]() ) при
) при ![]() =0. следовательно, найдется число r > 0 такое, что в круге
=0. следовательно, найдется число r > 0 такое, что в круге ![]()
![]() .
.
Отсюда вытекает, что в круге ![]() оператор-функция А(
оператор-функция А(![]() ) непрерывно обратима и, следовательно, уравнение (1) имеет единственное решение
) непрерывно обратима и, следовательно, уравнение (1) имеет единственное решение
![]() ,
,
при этом x(![]() ) аналитична в точке
) аналитична в точке ![]() =0 и радиус сходимости соответствующего степенного ряда равен min(
=0 и радиус сходимости соответствующего степенного ряда равен min(![]() , r). Для фактического построения x(
, r). Для фактического построения x(![]() ) удобно воспользоваться методом малого параметра. Будем разыскивать x(
) удобно воспользоваться методом малого параметра. Будем разыскивать x(![]() ) в виде
) в виде
![]() . (3)
. (3)
Подставляя ряд (3) в уравнение (1) и учитывая разложения (2), приходим к следующей системе для неопределенных коэффициентов x0, x1, x2, …:
А0x0 = y0, А0x1+А1x0 = y1,
А0x2 + А1x1 + А2x0 = y2, (4)
. . . . . . . . . . .
![]() , …
, …
Здесь А0 = А(0) непрерывно обратим. Решая последовательно уравнения получившейся системы, находим
![]() ,
, ![]() , … (5)
, … (5)
Возникающие здесь формулы довольно громоздки, однако этим путем можно найти решение уравнения с любой степенью точности. Метод малого параметра особенно удобен в тех случаях, когда обращение оператора А(0) – задача более простая, чем задача обращения оператора А(![]() ).
).
§8. Метод продолжения по параметру
Похожие работы
... математических методов, связанных с описанием и анализом типичных явлений, протекающих именно в электротехнических устройствах. 1 Применение преобразования Лапласа и его свойств к расчету переходных процессов Этот метод основан на преобразовании Лапласа. Пусть f(t) – оригинал, а F(p) – изображение этого оригинала по Лапласу. Для сокращения применяют такие обозначения: f(t)F(p), F(p)= Прямое ...
... лишь угловую часть лапласиана и имеет вид: . (6.23) Уравнение Лежандра, встречается в нескольких фундаментальных задачах: 1) в задаче о квантовых состояниях и энергетических уровнях ротатора - линейной молекулы, свободно вращающейся вокруг центра массы. 2) в уравнении Шрёдингера для атома H и водородоподобных ионов. 6.7.3. Уравнение Лежандра это вполне типичное операторное уравнение на
... плотность тока вероятности .(1.9) Из (1.9) следует, что j = 0 для всех функций , у которых функция Ф не зависит от координат. В частности, j= 0 для всех действительных функций . Решения уравнения Шредингера (1.1) в общем случае изображаются комплексными функциями. Использование комплексных функций весьма удобно, хотя и не необходимо. Вместо одной комплексной функции состояние системы можно ...
... популяции обязательно вырождаются, причем независимо от начального распределения особей по возрасту. В завершение рассмотрим пример. Одной из классических моделей динамики популяций является так называемая логистическая модель или модель Ферхюльста, которая описывается дифференциальным уравнением с начальным условием , где , см., например, [5, c. 14]. Если учитывать ограниченность времени жизни ...


0 комментариев