Формулировка основной теоремы

8.1. Формулировка основной теоремы

В качестве еще одного приложения теорем об обратных операторах рассмотрим один из вариантов метода продолжения по параметру. Пусть  и А непрерывно обратим. Если , то, согласно теореме 9 §3, В также непрерывно обратим. Оказывается, при определенных условиях можно доказать, что В будет непрерывно обратим и в том случае, когда он очень далек от А. Идея заключается в следующем. Рассмотрим непрерывную на отрезке [0, 1] оператор - функцию  такую, что А(0)=А, А(1)=В. Иначе говоря, в L(X, Y) рассматривается непрерывная кривая, соединяющая точки А и В. Будем предполагать, что для оператор – функции  выполняется следующее условие:

Существует постоянная  такая, что при всех  и при любых  справедливо неравенство

. (1)

Ниже будет доказана следующая теорема.

Теорема 14. Пусть А(λ) – непрерывная на [0, 1] оператор-функция (при каждом ), причем оператор А(0) непрерывно обратим. Если для А(λ)выполняется условие I, то А(I)непрерывно обратим, причем .

Замечание к теореме 14. Если выполнено условие I при  и оператор  непрерывно обратим, то

. (2)

Действительно, пусть , а , т.е.. тогда условие I дает  или , что означает справедливость неравенства (2).

8.2. Простейший случай продолжения по параметру

Приведем здесь доказательство теоремы 14 для случая, когда . Согласно условию этой теоремы . По замечанию 14 . Имеем следующую оценку:

.

Пусть , где . На [0, δ] имеем , и, следовательно, по теореме 9 А(λ) при всяком  непрерывно обратим. Если окажется, то , то теорема доказана.

Пусть δ < 1. Возьмем А(δ). Согласно замечанию п.14.1 . Повторяем наши рассуждения при λ>δ. Имеем оценку

,

если , откуда А(λ) непрерывно обратим при каждом . Если , то теорема доказана. Если же 2δ < 1, то  и рассуждение можно повторить. После конечного числа шагов мы достигаем точки λ=1, и, следовательно, А(1) непрерывно обратим.

Доказательство теоремы в общем случае

Рассмотренный выше частный случай отрезка в L(X,Y) не всегда удобен в приложениях. Общий случай основывается на следующем элементарном предложении.

Лемма. Пусть М – некоторое непустое множество на [0,1], одновременно открытое и замкнутое на [0.1]. тогда М=[0, 1].

Замечание 1. условие открытости М на [0,1] понимается так: для любого  существует δ > 0 такое, что .

Доказательство леммы. Пусть N = [0, 1] M (дополнение к М на [0, 1]). Нужно доказать, что N = Æ – пустое множество. Допустим противное, что N ¹ Æ. Поскольку М ¹ Æ и ограничено сверху, то существует b = supM, причем b Î M вследствие замкнутости. Покажем, что b = 1. Если b <1, то вследствие открытости M на [0, 1] найдется x > b, x Î M. Это противоречит определению supM. Следовательно, b >1 невозможно. Итак, 1Î М.

Теперь рассмотрим множество N. Как дополнение к М, оно также открыто и замкнуто на [0, 1], и, значит, к нему применимо рассуждение с supM . мы получаем, что 1 Î N. Это невозможно, ибо N – дополнение к М. полученное противоречие доказывает, что допущение N ¹ Æ неверно. Итак, N= Æ, т.е. М = [0, 1]. Лемма доказана.

Вернемся к доказательству теоремы. Пусть М – множество тех точек λÎ[0, 1], для которых оператор А(λ) непрерывно обратим. Согласно замечанию 1  для всех λ Î М. М не пусто, поскольку 0 Î [0, 1].

воспользуемся непрерывностью оператор–функции А(λ) в метрике L(X,Y). Для любого e > 0 найдется δ = δ(e)>0 такое, что при всех λ Î [0, 1] таких, что  < δ выполняется неравенство  <e.

Возьмем e = γ, тогда при  < δ(γ), λ Î [0, 1]

<1.

По теореме 9 §3 А(λ) непрерывно обратим для всех таких λ. Итак, вместе с λ0 М содержит , т.е. М открыто на [0, 1].

Докажем, что М замкнуто на [0, 1]. Пусть  и  при . Надо доказать, что λ0 М. воспользуемся неравенством  и получим

.

Вследствие непрерывности А(λ) по λ для любого e > 0 находим номер N = N(e) такой, что при n > N будет <e. Возьмем e = γ, тогда для n = N(γ)+1 <1.

По теореме 9 А(λ0) непрерывно обратим, т.е. λ0 Î М, и, значит, М замкнуто на [0, 1]. По лемме М = [0, 1] . в частности, 1Î М и . Теорема полностью доказана.

Замечание. Рассмотрим уравнение с параметром:

А(λ)х = у, λÎ [0, 1]. (1*)

Пусть для всех возможных решений этого уравнения при всяком λÎ [0, 1] справедлива оценка

, (2*)

где с – некоторая постоянная, не зависящая от х, у и λ. Оценка такого рода называется априорной оценкой для решения уравнения (1*). Очевидно, априорная оценка (2*) представляет собой лишь иначе записанное условие (1): .

Доказанная выше теорема свидетельствует о важности априорных оценок для доказательства теорем существования и единственности решений.

Глава 2. Приложение

Пример 1. Рассмотрим интегральное уравнение с малым вещественным параметром λ:

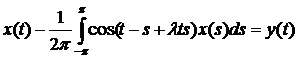 (1)

Это уравнение вида А()х = у() – операторное уравнение в С[-π; π], где

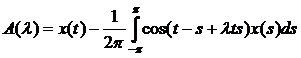
Покажем, что А() аналитична в т. 0, т.е. разлагается в ряд вида . Разложим функцию А() в ряд Тейлора: .

Найдем к – ую производную:

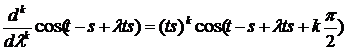
Разложим функцию в ряд Тейлора в т. 0:

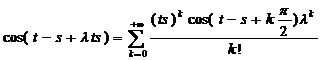
Таким образом, функция аналитична, следовательно, непрерывна при  = 0, а значит, уравнение имеет единственное решение.

Операторные коэффициенты имеют вид:

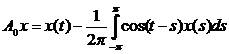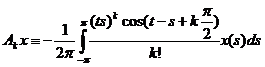;  (2)

I. Начнем с уравнения А0x0 = y системы (4) §7, где у нас теперь y0=y, yк=0, к ≥ 1.

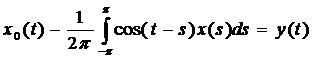
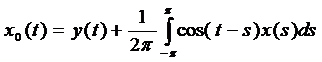
Заменим, , поэтому

, (4)

где

,  

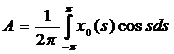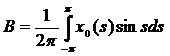
Для того, чтобы найти коэффициент А в уравнении (4), умножим его на cos t и, интегрируем по t от –π до π:

,

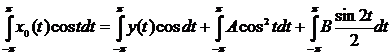подсчитаем интегралы:

, ,

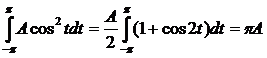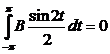
Тогда, подставив в уравнение, получаем: . Отсюда:

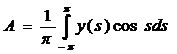. (5)

Найдем коэффициент В уравнения (4), умножив это уравнение на sin t и интегрируя по t от –π до π:

.

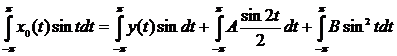Подсчитав соответствующие интегралы:

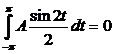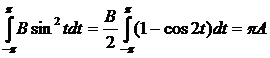, , , подставив и выразив В, получаем:

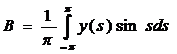. (6)

Подставим найденные коэффициенты (5) и (6) в уравнение (4):

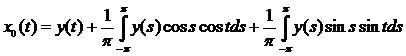
и свернем по формуле:

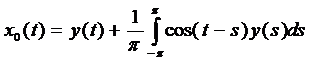
II. Найдем теперь x1(t), для этого необходимо решить следующее уравнение системы (4) §7: А0x1+А1x0 = y1. Так как y1=0 в нашем случае, то мы будем решать уравнение А0x1= – А1x0.

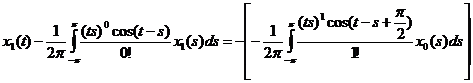
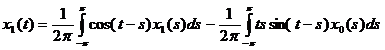
Обозначим 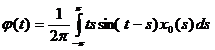, т.к. мы знаем теперь x0(s), следовательно φ(t) можно вычислить. Имеем:

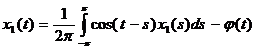
Как в предыдущем случае заменим, , поэтому

 . (7)

где , .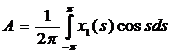

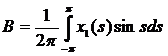Умножим уравнение (7) на cos t и проинтегрируем по t от –π до π – получим коэффициент А:

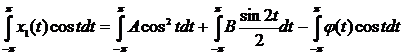
Подсчитав: , , ,

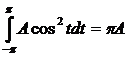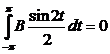имеем .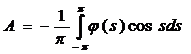

Аналогично умножив уравнение (7) на sin t и проинтегрируем по t от –π до π – получим коэффициент В: .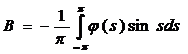

Составляем функцию x1(t), подставив коэффициенты А и В в уравнение и свернув равенство по формуле косинуса разности:

.

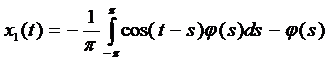Таким способом мы можем найти все остальные решения уравнения с любой степенью точности.

Пример 2. Применим метод продолжения по параметру для оценки разрешимости краевой задачи для дифференциального уравнения, а потом решим ее методом малого параметра.

–x'' + b(t)x' +c(t)x = y(t), 0< t <1, (1)

x(0) = x(1) = 0 (2)

Здесь c(t) непрерывна на [0, 1], b(t) непрерывно дифференцируема на [0, 1]. Предположим еще, что на [0, 1] c(t) – b(t)'/2 ≥ α > –8/π (*).

Покажем методом продолжения по параметру, что в этих условиях при всякой правой части y ÎY = С [0, 1] существует единственное решение задачи x Î X = С2 [0, 1] – пространству, состоящему из дважды непрерывно дифференцируемых на [0, 1] функций x(t), удовлетворяющих граничным условиям (2), и с нормой , где .

Запишем задачу (1) – (2) в операторном виде: Вx = y

Здесь  определен всюду на X со значениями в Y. В качестве оператора А примем ÎL(X, Y).

Соединим операторы А и В отрезком

, λ Î [0, 1].

Теперь необходимо установить априорную оценку для решений краевой задачи

–x'' + λb(t)x' + λc(t)x = y(t), 0< t <1, (3)

x(0) = x(1) = 0 (4)

Как только такая оценка будет получена, из теоремы п.8.1. будет следовать однозначная разрешимость краевой задачи (3) – (4).

Умножим уравнение (3) на x(t) и проинтегрируем полученное равенство по t от 0 до 1:

.

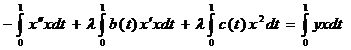Заметим, с учетом граничных условий:

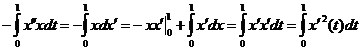
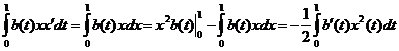
Подставим полученные интегралы и сгруппируем относительно λ:

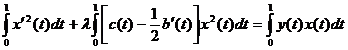 (5)

Произведем оценку всех трех слагаемых в этом равенстве.

Докажем, что 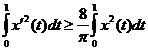. (6)

Заметим, что 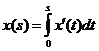, и значит по неравенству Коши – Буняковского:

.

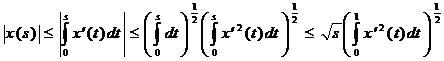Точно так же:

.

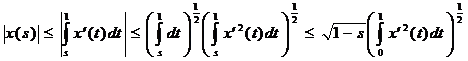Перемножим эти неравенства:

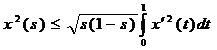. (6*)

Отсюда, замечая, что 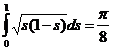, получим

 .

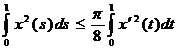
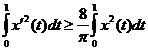Далее 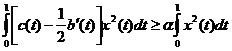 (7)

– это следует из предположения (*).

Последний интеграл равенства (5) можно оценить, используя скалярный квадрат:

, где .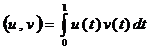

Для любого ε > 0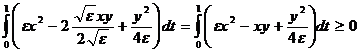   

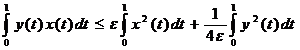. (8)

Используя полученные неравенства (6), (7), (8) и подставляя их в равенство (5), получаем:

,

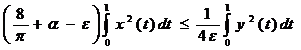считая ε > 0 достаточно малым, имеем

.

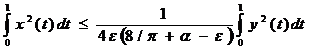Выберем  и получим

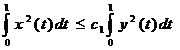, где .

Возвращаясь снова к равенству (5), получим следующую оценку:

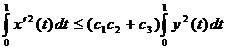, где , а .

Теперь с помощью оценки (6*) имеем 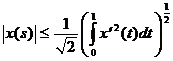 и, значит, учитывая, что 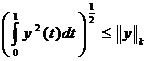, получим

 (9)

Из уравнения (3) можем получить оценки для  и :

. (10)

Здесь  оценивается через  и . Действительно, x(0) = x(1) = 0. по теореме Роля на (0, 1) найдется точка ξ, в которой x'(ξ) = 0. Тогда, запишем уравнение (3) в виде

,

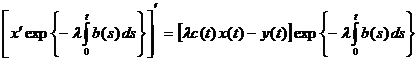(в этом можно убедиться, взяв производную:

 

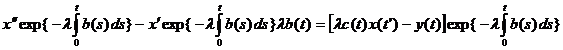
и сократив)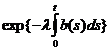

интегрируем его от ξ до θ и получим

.

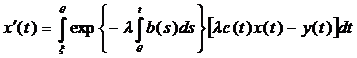Отсюда имеем оценку

, (11)

где .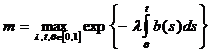

Теперь подставим полученные результаты в (10):

. (12)

Теперь (9), (11) и (12) дают искомую априорную оценку:

(постоянную с4 нетрудно подсчитать, сложив неравенства(9), (11), (12)и выполнив преобразования).

Таким образом, доказательство разрешимости задачи получено, теперь приступим к ее решению методом малого параметра.

Итак, рассмотрим операторное уравнение:

А(λ)x = y(λ),

где .

I. Начнем с уравнения А0x0 = y (где А0 – коэффициент при нулевой степени λ) системы (4) §7, причем y0 = y, yк = 0, к ≥ 1.

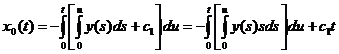 , причем с1 подбирается так, чтобы выполнялось краевое условие: x0(1) = 0.

II. Найдем x1(t), для этого необходимо решить следующее уравнение: А0x1+А1x0 = y1. Так как y1=0, то мы будем решать уравнение А0x1= – А1x0.

Из того, что следует следующее уравнение:

    

 .

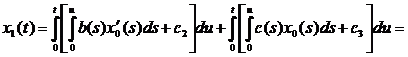
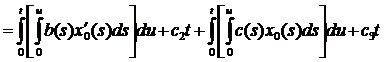По аналогии c2 и c3 подбираем так, чтобы выполнялось краевое условие: x0(1) = 0.

Таким образом, решения нашей краевой задачи выглядит так:

,

подставляя найденные решения, имеем:

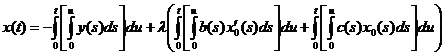
или

Список литературы

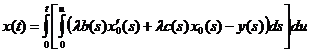
Данфорд Н., Шварц Дж. Линейные операторы. М., 1962

Талдыкин А.Т. Элементы прикладного функционального анализа: Учеб. пособие. – М.: Высшая школа, 1982.

Треногин В.А. Функциональный анализ. М., 1993.

Функциональный анализ./Под. ред. С. Г. Крейна. М., 1972

Хатсон В., Пим Дж. С. Приложения функционального анализа и теория операторов. Пер. с англ. – М.: Мир, 1