Навигация
Пусть будут заданы номера наборов четырех переменных, на которых логическая функция принимает единичное значение: f (2,5,6,7,10,12,13,14)=1
1. Пусть будут заданы номера наборов четырех переменных, на которых логическая функция принимает единичное значение: f (2,5,6,7,10,12,13,14)=1.
Выразим эту логическую функцию в СДНФ (символ конъюнкции писать не будем):
f (0010,0101, 0110, 0111, 1010, 1100, 1101, 1110) =
![]() .
.
На первом этапе минимизации исходную СДНФ можно упростить за счет использования закона склеивания, тогда получим:
![]() .
.
Обращаем внимание на то, что одну и ту же конституенту (импликанту) можно склеивать с другими конституентами (импликантами) многократно, так как в логике Буля действует закон идемпотентности:
![]() ,
,
поэтому любую конституенту можно размножить.
На втором этапе воспользуемся таблицей Куайна (табл. 8), в соответствии с которой данный метод минимизации получил свое наименование – метод Куайна. В таблице по вертикали перечислены все полученные на первом этапе упрощения импликанты, а по горизонтали – исходные конституенты. Единица в табл. 8 стоит там, где импликанта «накрывает» конституенту. Дело в том, что конституента всегда может быть заменена импликантой или даже отдельным термом по закону поглощения:
![]()
Таблица 8
|
| 0010 | 0101 | 0110 | 0111 | 1010 | 1100 | 1101 | 1110 |
| – – 1 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 0 1 – 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 1 1 – | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| – 1 0 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 1 0 – | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 1 – 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
После заполнения таблицы Куайна у нас получилось так, что почти в каждой графе оказалось по две единицы; между тем достаточно иметь одну единицу в графе. Поэтому, по возможности, нужно исключить избыточные единицы. Выбор единиц производится из соображений минимальности числа термов (выбранные единицы затемнены). В итоге оказалось, что можно обойтись только тремя импликантами вместо шести:
![]() .
.
С помощью таблиц истинности легко проверить, что полученная в МНФ функция воспроизводит все значения исходной функции. Отметим, что в общем случае решений по критерию минимума термов может быть несколько.
2. Не менее эффективным способом минимизации логических функций является метод сочетания индексов. Для его изложения составим табл. 9, в графах которой записаны возможные сочетания индексов. В последней графе выписаны значения функции. Анализ таблицы начинается слева по столбцам. Принцип исключения i, j‑кода следующий. На пересечении i‑столбца, например, с сочетанием индексов 23, и j‑строки, например, 3‑ей, находится код 10, что соответствует импликанте ![]() . Следовательно, в этом столбце везде, где встречается код 10, т. е. в строках 2, 3, 10 и 11, эти коды исключаются, поскольку значение функции в 3‑ей строке равно нулю. Теперь возьмем столбец с сочетанием индексов 124. Здесь во 2‑ой и 6‑ой строках оставлены коды 010, а в 10‑ой и 14‑ой строках – код 011. Сделано это потому, что эти коды встречаются только на строках со значением функции, равным единице. Напротив, код 110 этого же столбца встречается как при единичных значениях функции, так и при нулевых.
. Следовательно, в этом столбце везде, где встречается код 10, т. е. в строках 2, 3, 10 и 11, эти коды исключаются, поскольку значение функции в 3‑ей строке равно нулю. Теперь возьмем столбец с сочетанием индексов 124. Здесь во 2‑ой и 6‑ой строках оставлены коды 010, а в 10‑ой и 14‑ой строках – код 011. Сделано это потому, что эти коды встречаются только на строках со значением функции, равным единице. Напротив, код 110 этого же столбца встречается как при единичных значениях функции, так и при нулевых.
Таблица 9
| n | 1 | 2 | 3 | 4 | 12 | 13 | 14 | 23 | 24 | 34 | 123 | 124 | 134 | 234 | 1234 | y |
| 0 | 0 | 0 | 0 | 0 | 00 | 00 | 00 | 00 | 00 | 00 | 000 | 000 | 000 | 000 | 0000 | 0 |
| 1 | 1 | 0 | 0 | 0 | 10 | 10 | 10 | 00 | 00 | 00 | 100 | 100 | 100 | 000 | 1000 | 0 |
| 2 | 0 | 1 | 0 | 0 | 01 | 00 | 00 | 10 | 10 | 00 | 010 | 010 | 000 | 100 | 0100 | 1 |
| 3 | 1 | 1 | 0 | 0 | 11 | 10 | 10 | 10 | 10 | 00 | 110 | 110 | 100 | 100 | 1100 | 0 |
| 4 | 0 | 0 | 1 | 0 | 00 | 01 | 00 | 01 | 00 | 10 | 001 | 000 | 010 | 010 | 0010 | 0 |
| 5 | 1 | 0 | 1 | 0 | 10 | 11 | 10 | 01 | 00 | 10 | 101 | 100 | 110 | 010 | 1010 | 1 |
| 6 | 0 | 1 | 1 | 0 | 01 | 01 | 00 | 11 | 10 | 10 | 011 | 010 | 010 | 110 | 0110 | 1 |
| 7 | 1 | 1 | 1 | 0 | 11 | 11 | 10 | 11 | 10 | 10 | 111 | 110 | 110 | 110 | 1110 | 1 |
| 8 | 0 | 0 | 0 | 1 | 00 | 00 | 01 | 00 | 01 | 01 | 000 | 001 | 001 | 001 | 0001 | 0 |
| 9 | 1 | 0 | 0 | 1 | 10 | 10 | 11 | 00 | 01 | 01 | 100 | 101 | 101 | 001 | 1001 | 0 |
| 10 | 0 | 1 | 0 | 1 | 01 | 00 | 01 | 10 | 11 | 01 | 010 | 011 | 001 | 101 | 0101 | 1 |
| 11 | 1 | 1 | 0 | 1 | 11 | 10 | 11 | 10 | 11 | 01 | 110 | 111 | 101 | 101 | 1101 | 0 |
| 12 | 0 | 0 | 1 | 1 | 00 | 01 | 01 | 01 | 01 | 11 | 001 | 001 | 011 | 011 | 0011 | 1 |
| 13 | 1 | 0 | 1 | 1 | 10 | 11 | 11 | 01 | 01 | 11 | 101 | 101 | 111 | 011 | 1011 | 1 |
| 14 | 0 | 1 | 1 | 1 | 01 | 01 | 01 | 11 | 11 | 11 | 011 | 011 | 011 | 111 | 0111 | 1 |
| 15 | 1 | 1 | 1 | 1 | 11 | 11 | 11 | 11 | 11 | 11 | 111 | 111 | 111 | 111 | 1111 | 0 |
Итак, все коды на строках, заканчивающихся нулевыми значениями функции, исключаются автоматически. Если эти коды попадают на строки, заканчивающиеся единичным значением функции, то они также не учитываются. Остаются только те коды, которые расположены на строках с единичным значением функции (эти коды затемнены).
Далее руководствуются следующим правилом. Для того чтобы функция приняла значение, равное единице, достаточно того, чтобы только какая-нибудь одна импликанта на строке приняла единичное значение. Прежде всего, оставляем минимальную импликанту ![]() , которая перекрывает единицы в строках 2, 6, 10 и 14. Затем, естественно, обращаемся к 12‑ой строке. Здесь оставляем единственный на строке код 011, что отвечает импликанте
, которая перекрывает единицы в строках 2, 6, 10 и 14. Затем, естественно, обращаемся к 12‑ой строке. Здесь оставляем единственный на строке код 011, что отвечает импликанте ![]() . Эта же импликанта ответственна за 13‑ую строку, оканчивающуюся тоже единицей. Осталось рассмотреть 5‑ую и 7‑ую строки. Общей для них является импликанта:
. Эта же импликанта ответственна за 13‑ую строку, оканчивающуюся тоже единицей. Осталось рассмотреть 5‑ую и 7‑ую строки. Общей для них является импликанта: ![]() . Таким образом, тремя импликантами мы перекрыли все единичные значения функции, что совпадает с результатом, полученным на основе таблиц Куайна.
. Таким образом, тремя импликантами мы перекрыли все единичные значения функции, что совпадает с результатом, полученным на основе таблиц Куайна.
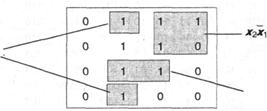
3. Существует графический способ склеивания, который получил название метод карты Карно (представлен в табл. 10). Выделяем смежные единицы, это и будут слагаемые нашей функции.
Таблица 10
| x3x4 x1x2 | 00 | 01 | 11 | 10 |
| 00 | 0 | 0 | 1 | 1 |
| 01 | 1 | 0 | 0 | 0 |
| 11 | 1 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 |
![]() – получили два слагаемых
– получили два слагаемых
Хотя табл. 9 более громоздка, чем табл. 8, метод сочетания индексов не считается более сложным, чем метод Куайна, если помнить, что до составления таблиц Куайна необходимо произвести многочисленные склейки конституент и импликант. Реализация на компьютере алгоритма метода сочетания индексов оказывается сравнительно простой. И напротив, внешняя простота и наглядность третьего метода минимизации логических функций с помощью карт Карно оборачивается сложной программой при реализации алгоритма на компьютере.
Таблица 11
|
|
|
|
| ||
|
| 1100 | 1110 | 0110 | 0100 |
|
|
| 1101 | 1111 | 0111 | 0101 |
|
|
| 1001 | 1011 | 0011 | 0001 |
|
|
| 1000 | 1010 | 0010 | 0000 |
|
|
|
|
|
|
Таблица 12
![]()
![]()
Карта Карно для четырех переменных представлена в виде табл. 11. Каждая клетка карты соответствует конституенте. Заполненная карта представлена табл. 12 (функция взята та же, что и в первых двух методах). Согласно закону склеивания, две смежные конституенты с единичными значениями всегда можно объединить для получения соответствующей импликанты. Причем смежными считаются и те, которые лежат на границах карты. Какие именно единицы требуется объединить для получения подходящей импликанты, легко определить визуально. Следует также помнить, что в соответствии с законом идемпотентности одна и та же единица табл. 12 может склеиваться с двумя или тремя смежными единицами.
Контрольные вопросы1. Перечислите основные методы минимизации функций.
2. Расскажите о методе Куайна.
3. Расскажите о методе карт Карно.
3.9 Неполностью определенные логические функцииРанее мы рассматривали ситуации, когда на множество аргументов или логических переменных x1, x2,…, xn не накладывались ограничения, или, что то же самое, функции были определены на всем наборе аргументов. Однако реально на практике функции либо не определены полностью, либо есть запрещенные комбинации. Необходимо доопределить функцию таким образом, чтобы аналитическая форма ее представления была минимальной, далее производят склейки (пример приведён в табл. 13).
Таблица 13
| x3x4 x1x2 | 00 | 01 | 11 | 10 |
| 00 | 0* | 0 | 1* | 0 |
| 01 | 1* | 1 | 1 | 1* |
| 11 | 0 | 0 | 1 | 0* |
| 10 | 0* | 0* | 1* | 0* |
![]() .
.
* – эти значения доопределили сами, исходя того, чтобы выражение для функции F было минимальным.
3.10 Формы представления булевых функцийК настоящему времени мы знакомы с двумя формами представления булевых функций: таблица истинности и формула (аналитическая запись). Рассмотрим еще две формы представления таких функций.
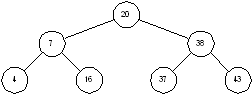
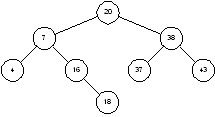
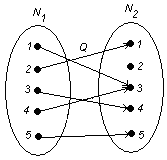
3.10.1 Семантические деревьяСемантическое дерево – это двоичное дерево, корень которого помечен двоичной функцией от m переменных, из каждого узла идут по два ребра, соответствующих двум значениям очередной переменной, а 2m листьев помечены соответствующими значениями функции.
3.10.2 Бинарные диаграммы решений (БДР)
Бинарная диаграмма решений (Binary Decision Diagrams, BDD) – это граф, являющийся модификацией семантического дерева. В БДР узлы с одним и тем же значением функции объединены. Если на каждом уровне БДР все вершины имеют одну и ту же метку (одинаковые переменные), то такая БДР называется упорядоченной (в англоязычной литературе такое представление называется Ordinary Binary Decision Diagrams, или сокращенно OBDD). Будем называть такое представление УБДР. Вершины УБДР расположены по уровням, каждому уровню соответствует одна переменная, которая помечает вершины, находящиеся на этом уровне. Из каждой вершины выходят два ребра: одно соответствует нулевому значению соответствующей переменной (будем его изображать штриховой линией), а другое – единичному значению этой переменной (оно изображается сплошной линией).
На рис. 4 показаны все четыре формы представления функции ![]() .
.
Бинарные диаграммы решений используются как компактная форма представления булевой функции. Такое представление полезно во многих случаях, например, когда нужно многократно вычислять значения функции при различных наборах значений ее аргументов. Для того чтобы получить значение функции f, например, на языке С, вместо хранения громоздкой таблицы истинности можно вычислить оператор: f=q? (r? 0:1): (р? 0:1), который построен на основании БДР (см. рис. 4). В этом примере использование УБДР позволяет вычислить значение булевой функции, выполнив всего две операции, в то время как при ее вычислении по аналитическому представлению требуется не менее 5 операций.
Рис. 4. Четыре формы представления двоичной функции
| f (p, q, r) | Таблица истинности | Семантическое дерево | Бинарная диаграмма решений | ||||||||||||||||||||||||||||||||||||
|
|
|
|
|
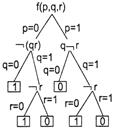
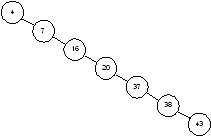
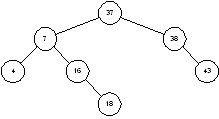
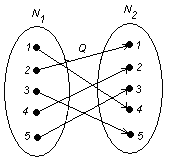
Сложность представления функции с помощью УБДР существенно зависит от порядка переменных. Так, например, УБДР для иного порядка переменных, чем на рис. 4, содержит четыре вершины, а не три (рис. 5). Интересной проблемой теоретической информатики является нахождение алгоритма, дающего оптимальный порядок переменных булевой функции с точки зрения представления этой функции упорядоченной БДР.
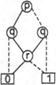
Рис. 5. УБДР для функции ![]() с порядком переменных [p, q, r]
с порядком переменных [p, q, r]
При синтезе логических схем применяют элементы с одним и несколькими входами. Условия функционирования таких элементов определяются переключательными функциями одной или нескольких переменных.
Входные и выходные сигналы логических схем зависят от времени (одни из них в некоторый момент времени равны 1, в другие моменты времени 0). Логические функции, описывающие работу таких схем, называют переменными. Используют также схемы, для которых во все моменты времени сигналы равны либо 1, либо 0. Логические функции, описывающие работу этих схем, называют постоянными.
Существует только четыре различные переключательные функции одной переменной. Как видно из таблицы 14, только две функции не зависят от переменной А (в этих случаях переменная А фиктивна).
Таблица 14
| Х | А | Условное обозначение | Название функции |
| 0 1 | |||
| X0=f0 (A) X1=f1 (A) X2=f2 (A) X3=f3 (A) | 0 0 0 1 1 0 1 1 | 0 A
1 | Константа 0 Переменная А Инверсия А Константа 1 |
Для функции двух переменных существует шестнадцать различных переключательных функций. Как видно из таблицы 5, только десять функций существенно зависят от переменных А и В.
На рис. 6, 7 приведены обозначения элементов, реализующих некоторые переключательные функции двух переменных.
Каждой элементарной логической операции можно поставить в соответствие элементарную логическую схему или вентиль. На входе и выходе вентиля мы имеем логические сигналы двух видов, что можно ассоциировать с логическим 0 или логической 1.
Похожие работы
элементы теории нечетких множеств можно применять для решения экономических задач в условиях неопределённости. 1. применение Логических функций 1.1 Применение методов дискретной математики в экономике При исследовании, анализе и решении управленческих проблем, моделировании объектов исследования и анализа широко используются методы формализированного представления, являющегося предметом ...
... подход к разработке эффективного алгоритма для решения любой задачи – изучить ее сущность. Довольно часто задачу можно сформулировать на языке теории множеств, относящейся к фундаментальным разделам математики. В этом случае алгоритм ее решения можно изложить в терминах основных операций над множествами. К таким задачам относятся и задачи информационного поиска, в которых решаются проблемы, ...
... которой были разработаны в последней четверти 19 века Георгом Кантором. Цель контрольной работы – ознакомится с основными понятиями и методами решения по дискретной математике, уметь применить полученные знания при решении практического задания. Задание 1 Представить с помощью кругов Эйлера множественное выражение . Используя законы и свойства алгебры множеств, упростить заданное ...
в и формальных систем является центральной в дисциплине. В настоящие время от нее возникли ответвления, например, разработка алгоритмических языков программирования.Одной из важнейших проблем в дискретной математики является проблема сложности вычислений.Теория сложности вычислений помогает оценить расход времени и памяти при решении задач на ЭВМ. Теория сложности позволяет выделить объективно ...
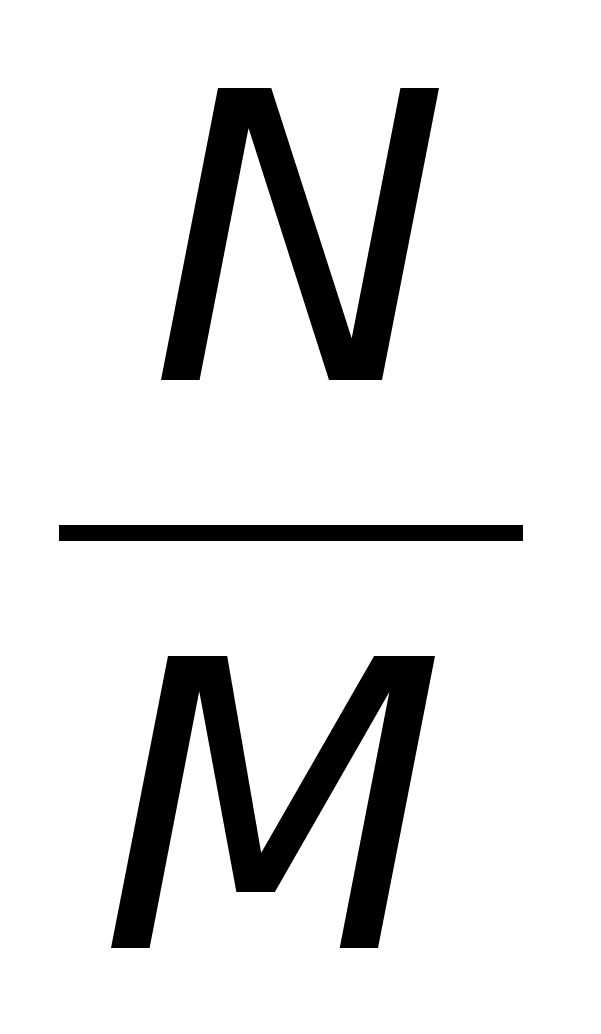
0 комментариев