Навигация
Конечные автоматы без памяти (комбинационные)
3.12.2.1 Конечные автоматы без памяти (комбинационные)
Общая формула, описывающая этот вид автоматов:
![]() , i = 1, 2, …, k.
, i = 1, 2, …, k.
![]() – в векторной форме
– в векторной форме
Пример 1.
Примером таких автоматов является простая экспертная система профессиональной пригодности, где входные значения – это ответы на n вопросов, а выходные – k выводов о том, может ли человек работать в данной области.
Пример 2.
Диагностика неисправностей, заболеваний и т. д.
Пример 3.
Пусть функционирование логического автомата описывается формулой:
![]() .
.
На языке Pascal оператор присваивания, соответствующий этой формуле:
![]()
Для более сложной модели получается структура типа запись:
Type
Prep = record
Number: Integer;
Stroka: String;
Zn: Boolean;
End;
Далее моделируется базис, который будет работать с этими высказываниями. Для каждой логической операции пишем процедуру или функцию.
Function otr (a: prep; var b: prep; параметры сохранения и т. д.): Boolean;
Function con (a, b: prep; var c: prep; параметры сохранения и т. д.): Boolean;
Function diz (a, b: prep; var c: prep; параметры сохранения и т. д.): Boolean;
Пример 4.
Отмоделировать функцию Yi:
![]()
Высказывание моделируется записью:
Function y1 (x1, x2, x3, x4: prep; var rez: prep; sohr: Boolean; newnumber: Integer; t: String): Boolean;
Var
I: boolean; a, b, c, d, e,: prep;
Begin
I:= otr(x1, a, false, 0);
I:= otr(x2, b, false, 0);
I:= con (a, b, c, false, 0);
I:= con (c, x3, d, false, 0);
I:= otr(x3, a, false, 0);
I:= otr(x4, a, false, 0);
I:= con(x2, a, c, false, 0);
I:= con (c, b, e, false, 0);
I:= diz (d, e, rez, false, 0);
If sohr then begin
rez.number:=newnumber;
rez.stroka:=t;
end;
y1:=rez.znachenie;
end;
Отмоделировать функцию лучше программным путем, т. к. программу довольно просто модифицировать.
3.12.2.2 Конечные автоматы с памятью (последовательностные)
Для таких автоматов характерно наличие вектора внутренних состояний z=(z1, z2,…, zm).
В таких автоматах каждая логическая функция зависит от входных функций x и функций внутреннего состояния z.

Рис. 10. Конечный автомат с памятью
![]()
![]() . (8)
. (8)
Для автоматов с памятью характерно, что они функционируют во времени, и в момент времени t0 должно быть задано начальное состояние z0. В момент времени t0![]() определяется выражением (8). В момент времени t1=t0+t входной вектор может поменяться, в свою очередь может поменяться вектор состояний Y.
определяется выражением (8). В момент времени t1=t0+t входной вектор может поменяться, в свою очередь может поменяться вектор состояний Y.
![]() , (9)
, (9)
где t – такт логического конечного автомата. Считается, что t много больше времени расчета на ЭВМ.
Пример.
Та же самая экспертная система определения профессиональной пригодности, но с условием, что значение о профессиональной пригодности зависит от ранее полученных ответов. Такие экспертные системы называют самообучающимися, т. к. сразу правильного ответа не дают. Частным случаем конечного автомата с памятью является автомат с обратной связью по выходу. Для него вектор внутренних состояний в момент времени t+t равен вектору выходных сообщений в момент времени t. Пример конечного автомата с памятью и обратной связью по выходу приведен на рис. 11.
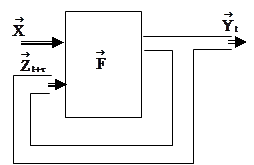
Рис. 11. Конечный автомат с памятью и обратной связью по выходу
Экспертная система является примером конечного автомата с памятью с обратной связью по выходу. Программная модель такого автомата базируется на программной модели автомата без памяти, однако, помимо уже накопленного опыта добавляется процедура tact, а также начальные значения входных и выходных переменных.
Const
N=…; k=…;
Type
Vector x = array [1..n] of boolean;
Vector y = array [1..k] of boolean;
Var
X: vector X;
Ypred, Y: vector Y;
Procedure tact (v: vector X; var Ypred, Y: vector Y);
Var
I: integer;
Begin
Y[1]:=y1(…);
Y[2]:=y2(…);
Y[3]:=y3(…);
Y[k]:=yk(…);
For i:=1 to k do
Ypred[i]:= Y[i];
End;
End.
Состояние конечного автомата называется установившимся, если с течением времени при постоянном значении входного вектора Х, вектор Y принимает постоянное значение. В этом случае процесс обучения конечного автомата заканчивается, и результаты его работы могут быть использованы. Однако существуют автоматы, состояние которых не устанавливается с течением времени. Такие автоматы используются только в схемотехнике. Примером такого автомата является автомат триггерного типа. Логическая схема триггера приведена на рис. 12.
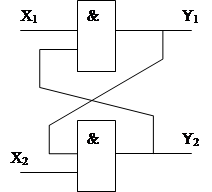
Рис. 12. Автомат триггерного типа
Другим частным случаем является автономный конечный автомат, для которого вектор входных воздействий ![]() отсутствует. Для него вектор выходных состояний является функцией от вектора внутренних состояний
отсутствует. Для него вектор выходных состояний является функцией от вектора внутренних состояний ![]() . Для него
. Для него ![]() (с обратной связью по выходу), тогда
(с обратной связью по выходу), тогда ![]() . Такие конечные автоматы называют также генераторами высказываний или генераторами логической последовательности. Они могут использоваться для отладки и моделирования некоторых ситуаций.
. Такие конечные автоматы называют также генераторами высказываний или генераторами логической последовательности. Они могут использоваться для отладки и моделирования некоторых ситуаций.
1. Что такое логический конечный автомат?
2. Представьте в виде рисунка логический конечный автомат.
3. Что такое такт конечного логического автомата?
4. Приведите пример конечного автомата без памяти.
5. Приведите пример конечного автомата с памятью.
6. Приведите пример конечного автомата с обратной связью по выходу.
Библиографический список
1. Акимов В.А. Дискретная математика: логика, группы, графы. М.: Лаборатория Базовых Знаний, 2003, 376 с.
2. Стол Роберт Р. Множества. Логика. Аксиоматические теории. Пер. с англ. Ю.А. Гастева И.Х. Шмаина. Под ред. Ю.А. Шихановича. М., «Просвещение», 1968, 232 с.
3. Ершов Ю.А., Полюнин Е.А. Математическая логика: Учебное пособие для вузов. М.: Наука. Гл. ред. физ. – мат. лит., 1987, 336 с.
4. Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. М.: Высшая школа, 2003, 256 с.
5. Р. Хаггарти Дискретная математика для программистов Москва: Техносфера, 2003, 320 с.
6. Гончарова Г.А., Мочалин А.А. Элементы дискретной математики: Учебное пособие. – М.: ФОРУМ: ИНФРА-М, 2004, 128 с.
7. Судоплатов С.В., Овчинникова Е.В. Элементы дискретной математики: Учебник. – М.: ИНФРА – М; Новосибирск: НГТУ, 2003, 280 с. – (Серия «Высшее образование»)
8. Новиков Ф.А. Дискретная математика для программистов. – СПб: Питер, 2001, 304 с.: ил.
Похожие работы
элементы теории нечетких множеств можно применять для решения экономических задач в условиях неопределённости. 1. применение Логических функций 1.1 Применение методов дискретной математики в экономике При исследовании, анализе и решении управленческих проблем, моделировании объектов исследования и анализа широко используются методы формализированного представления, являющегося предметом ...
... подход к разработке эффективного алгоритма для решения любой задачи – изучить ее сущность. Довольно часто задачу можно сформулировать на языке теории множеств, относящейся к фундаментальным разделам математики. В этом случае алгоритм ее решения можно изложить в терминах основных операций над множествами. К таким задачам относятся и задачи информационного поиска, в которых решаются проблемы, ...
... которой были разработаны в последней четверти 19 века Георгом Кантором. Цель контрольной работы – ознакомится с основными понятиями и методами решения по дискретной математике, уметь применить полученные знания при решении практического задания. Задание 1 Представить с помощью кругов Эйлера множественное выражение . Используя законы и свойства алгебры множеств, упростить заданное ...
в и формальных систем является центральной в дисциплине. В настоящие время от нее возникли ответвления, например, разработка алгоритмических языков программирования.Одной из важнейших проблем в дискретной математики является проблема сложности вычислений.Теория сложности вычислений помогает оценить расход времени и памяти при решении задач на ЭВМ. Теория сложности позволяет выделить объективно ...
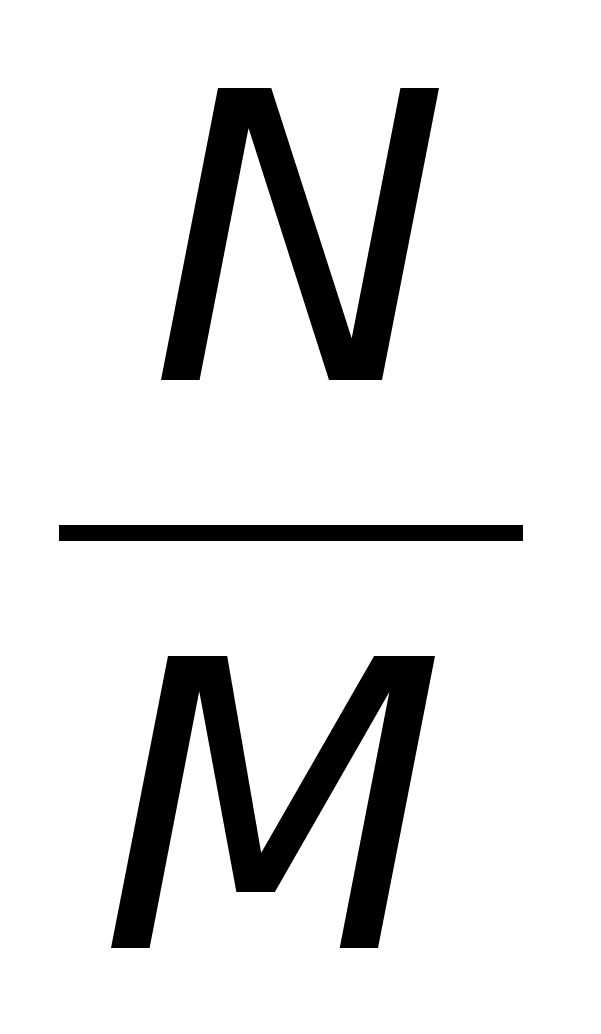
0 комментариев