Навигация
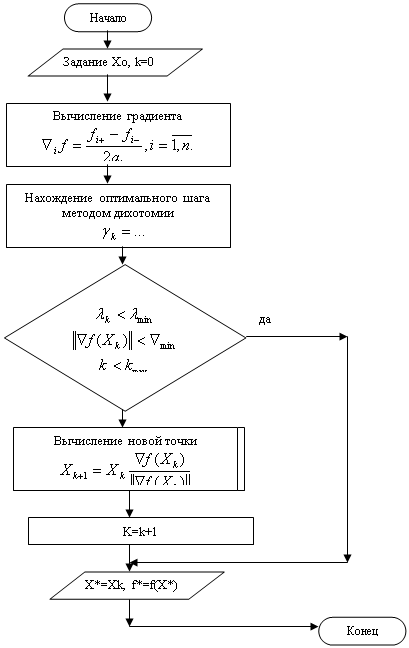
Методы безусловной многомерной оптимизации
Федеральное агентство по образованию
Новокузнецкий филиал-институт
ГОУ ВПО «Кемеровский государственный университет»
Кафедра информационных систем и управления им. В.К. Буторина
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Теория управления»
Методы безусловной многомерной оптимизации
(Вариант 20)
Выполнили: студенты IV курса
группы ПИЭ - 061
Тимохова А.В.
Годун И.А.
Руководитель: ассистент
кафедры ИСУ
Щепетов
Алексей
Викторович
Новокузнецк 2009
1 Задача об оптимальном распределении инвестиций
Задача: Распределить Т = 100 ден.ед. по четырем предприятиям с целью получения максимальной суммарной прибыли. Прибыль с предприятий задается таблицей 1.1.
Таблица 1.1
| X | g1 | g2 | g3 | g4 |
| 0 | 0 | 0 | 0 | 0 |
| 20 | 11 | 24 | 12 | 35 |
| 40 | 26 | 22 | 28 | 33 |
| 60 | 31 | 32 | 37 | 36 |
| 80 | 42 | 41 | 47 | 40 |
| 100 | 58 | 59 | 53 | 54 |
Процесс оптимизации разобьем на n шагов (в нашей задаче n =4). На k-м шаге будем оптимизировать инвестирование не всех предприятий, а только с k-го по n-е. При этом на них расходуются не все средства, а некоторая меньшая сумма Ck≤Т, которая и будет являться переменной состояния системы. Переменной управления на k-м шаге назовем величину xk средств, вкладываемых в k-ое предприятие. В качестве функции Беллмана Fk(Ck) на k-м шаге в этой задаче можно выбрать максимально возможную прибыль, которую можно получить с предприятий с k-го по n-е при условии, что на их инвестирование осталось Ck средств. Очевидно, что при вложении в k-е предприятие xk средств получим прибыль gk(xk), а система в (k+1)-му шагу перейдет в состояние Ck+1 = Ck – xk, т.е. на инвестирование предприятий с (k+1)-ого до n-го останется Ck+1 средств.
Таким образом, на первом шаге условной оптимизации при k=n функция Беллмана представляет собой прибыль только с n-го предприятия. При этом на его инвестирование может выделяться количество средств Ck, 0≤Ck≤Т. Очевидно, чтобы получить максимум прибыли с этого последнего последнего предприятия, надо вложить в него все эти средства, т.е. Fn(Cn)=gn(Cn) и xn=Cn.
На каждом из последующих шагов для вычисления функции Беллмана следует использовать результаты предыдущего шага. Максимально возможная прибыль, которая может быть получена предприятиями с k-го по n-е, равна:
![]() .
.
Максимум этого выражения достигается на некотором значении x*k, которое и является оптимальным управлением на k-м шаге для состояния системы Ck. Аналогично можно отыскать функции Беллмана и оптимальные управления вплоть до шага k=1.
Функция Беллмана F1(C1) представляет собой максимально возможную прибыль со всех предприятий (с 1-го по n-е), а значение x*k, на котором достигается максимум прибыли, является оптимальным количеством средств, которые необходимо вложить в 1-е предприятие. Далее, для всех последующих шагов вычисляется величина Ck = Ck-1 – Xk и оптимальным управлением на k-м шаге является то значение Xk, которое доставляет максимум прибыли при соответствующем состоянии системы Ck.
Решение.
Этап I. Условная оптимизация.
Шаг 1. k = 4. Предполагаем, что все средства 100 ден.ед. переданы на инвестирование третьего предприятия. В этом случае максимальная прибыль составит F4(C4) = 54, см. таблицу 1.2.
Таблица 1.2
| С4 | x4 | F4(C4) | X*4 | |||||
| 0 | 20 | 40 | 60 | 80 | 100 | |||
| 0 | 0 | – | – | – | – | – | 0 | 0 |
| 20 | – | 35 | – | – | – | – | 35 | 20 |
| 40 | – | – | 33 | – | – | – | 33 | 40 |
| 60 | – | – | – | 36 | – | – | 36 | 60 |
| 80 | – | – | – | – | 40 | – | 40 | 80 |
| 100 | – | – | – | – | – | 54 | 54 | 100 |
Шаг 2. k = 3. Определяем оптимальную стратегию инвестирования во второе и третье предприятия. При этом рекуррентное соотношение Беллмана будет иметь вид:
![]() .
.
На его основании рассчитываются данные таблицы 1.3.
Таблица 1.3
| С3 | x3 | F3(C3) | X*3 | |||||
| 0 | 20 | 40 | 60 | 80 | 100 | |||
| 0 | 0 | 0 | 0 | |||||
| 20 | 35 | 12 | 35 | 0 | ||||
| 40 | 33 | 47 | 28 | 47 | 20 | |||
| 60 | 36 | 45 | 63 | 37 | 63 | 40 | ||
| 80 | 40 | 48 | 61 | 72 | 47 | 72 | 60 | |
| 100 | 54 | 52 | 64 | 70 | 82 | 53 | 82 | 80 |
Шаг 3. k = 2. Определяем оптимальную стратегию инвестирования в первое и остальные предприятия. При этом рекуррентное соотношение Беллмана будет иметь вид:
![]() .
.
На его основе находятся данные таблицы 1.4.
Таблица 1.4
| С2 | x2 | F2(C2) | X*2 | |||||
| 0 | 20 | 40 | 60 | 80 | 100 | |||
| 0 | 0 | 0 | 0 | |||||
| 20 | 35 | 24 | 35 | 0 | ||||
| 40 | 47 | 59 | 22 | 59 | 20 | |||
| 60 | 63 | 71 | 57 | 32 | 71 | 20 | ||
| 80 | 72 | 87 | 69 | 67 | 41 | 87 | 20 | |
| 100 | 82 | 96 | 85 | 79 | 76 | 59 | 96 | 20 |
Шаг 4. k = 1. Определяем оптимальную стратегию инвестирования в первое и остальные предприятия. При этом рекуррентное соотношение Беллмана будет иметь вид:
![]() .
.
На его основе находятся данные таблицы 1.5.
Таблица 1.5
| С1 | x1 | F1(C1) | X*1 | |||||
| 0 | 20 | 40 | 60 | 80 | 100 | |||
| 0 | 0 | 0 | 0 | |||||
| 20 | 35 | 11 | 35 | 0 | ||||
| 40 | 59 | 46 | 26 | 59 | 0 | |||
| 60 | 71 | 70 | 61 | 31 | 71 | 0 | ||
| 80 | 87 | 82 | 85 | 66 | 42 | 87 | 0 | |
| 100 | 96 | 98 | 97 | 90 | 77 | 58 | 98 | 20 |
Этап II. Безусловная оптимизация.
Шаг 1. По данным таблицы 1.5 максимальный доход при распределении 100 ден.ед. между тремя предприятиями составляет F1= 98. При этом первому предприятию нужно выделить x1 = 20 ден.ед.
Шаг 2. Определяем величину оставшихся денежных средств, приходящуюся на долю второго и третьего предприятий:
С2 = С1 – x*1 = 100 – 20 = 80.
По данным таблицы 1.4 находим, что оптимальный вариант распределения денежных средств размером 80 ден.ед. между вторым, третьим и четвертым предприятиями составляет F2 = 96 ден.ед. при выделении второму x2 = 20 ден.ед.
Шаг 3. Определяем величину оставшихся денежных средств, приходящуюся на долю третьего и четвертого предприятия:
С3 = С2 – x*2 = 80 – 20 = 60.
Из таблицы 1.3 находим F3 = 63 и x*3 = 40 ден.ед. При этом получается что x*4 = 20 ден.ед. и F4 = 35.
Таким образом, оптимальный план инвестирования предприятий
X* = (20,40,20,20),
обеспечивающий максимальный доход
F(100) = g1(20) + g2(40) + g3(20) + g4(20) = 11 + 24 + 28 + 35 = 98 ден.ед.
Ответ: Максимальная суммарная прибыль по четырем предприятиям составляет 98 ден.ед.
Похожие работы
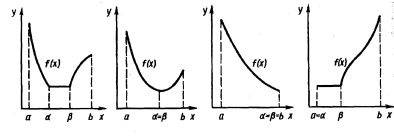
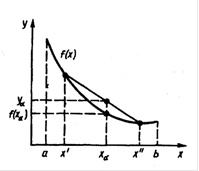
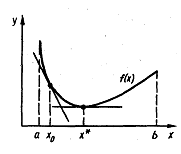
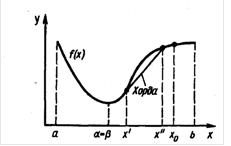
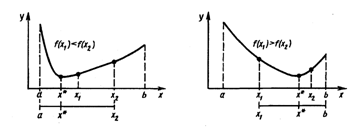
... 4 - график унимодальной, но не выпуклой функции Таким образом, кроме перечисленных свойств, выпуклые функции обладают также и всеми свойствами унимодальных функций. 2. Прямые методы безусловной оптимизации Для решения задачи минимизации функции f (х) на отрезке [а; b] на практике, как правило, применяют приближенные методы. Они позволяют найти решение этой задачи с необходимой точностью ...
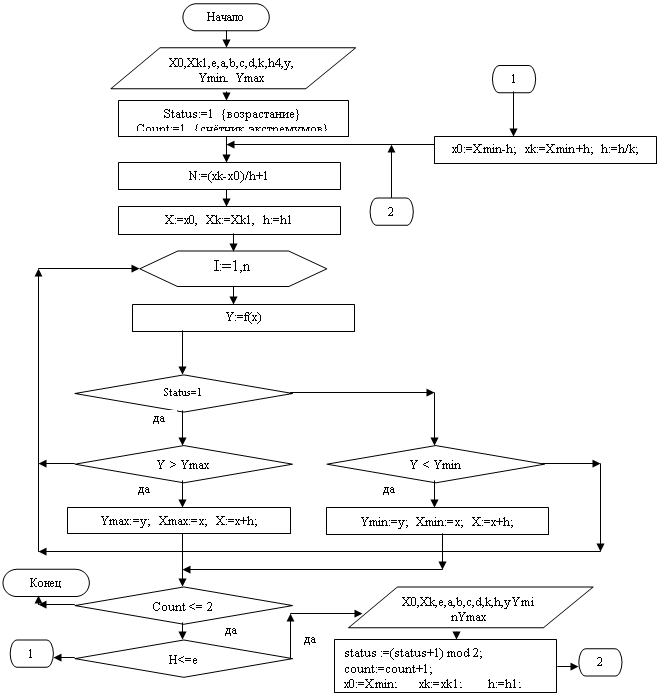
... : т.е. . Для определения координат точки Х1 нужно выбрать значение шага . Получим : Из соотношения (,)=0 имеем: (-3-3)(-3)+(1+)=10+10=0 откуда = Задание 4 ПРИМЕНЕНИЕ ГРАДИЕНТНЫХ МЕТОДОВ ДЛЯ ОПТИМИЗАЦИИ НА ЭВМ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ОБЪЕКТОВ Цель задания: приобрести практические навыки разработки алгоритмов и программ оптимизации математических моделей градиентным методом. ...
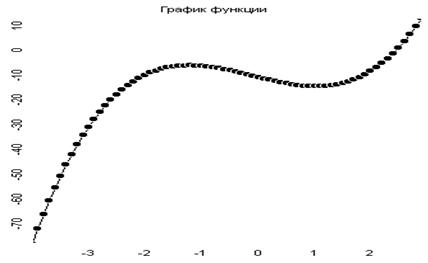
... от года-x и от номера месяца в году-y следующим образом: F(x)=50-x2+10x-y2+10y. Определите, в каком году и в каком месяце прибыль была максимальной. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МЕТОДЫ ОПТИМИЗАЦИИ Билет № 22 1) Постановка вариационной задачи с ограничениями. Привести пример. 2) Дайте геометрическую ...
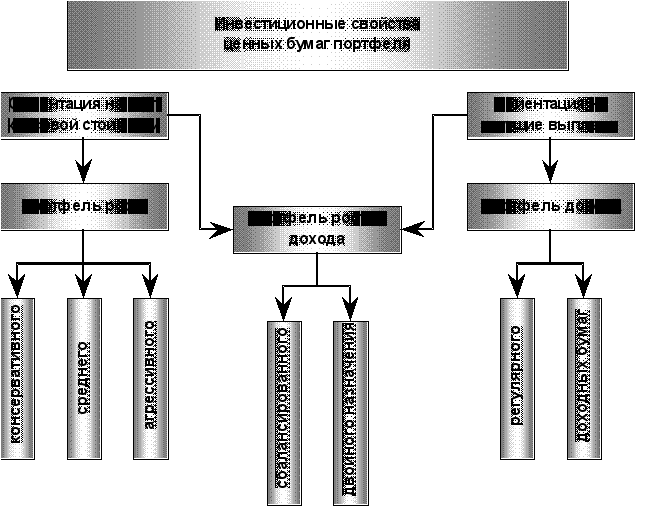
... , портфель ценных бумаг является тем инструментом, с помощью которого инвестору обеспечивается требуемая устойчивость дохода при минимальном риске. 3. ПРИНЦИПЫ ФОРМИРОВАНИЯ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ При формировании инвестиционного портфеля следует руководствоваться следующими соображениями: безопасность вложений (неуязвимость инвестиций от потрясений на рынке инвестиционного капитала), ...

0 комментариев