Навигация
Провести процедуру структурно-параметрической идентификации математической модели для исходных данных. Оценить адекватность
1. Провести процедуру структурно-параметрической идентификации математической модели для исходных данных. Оценить адекватность.
2. Проанализируйте данные, исключив повторы. Ответьте на вопросы: изменилось ли математическая модель? Как изменился коэффициент детерминации? Адекватна ли подобранная модель данным?
Решение:
Построим график эмпирических данных (рисунок 4).
Рисунок 4- График эмпирических данных
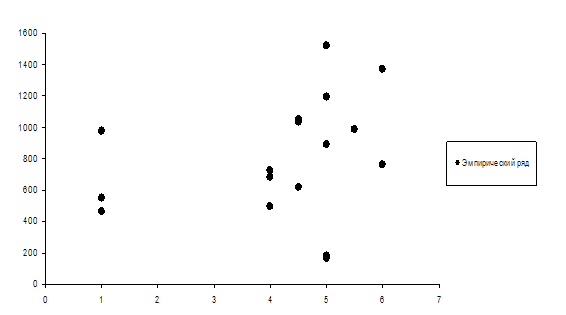
Проведем все необходимые расчеты для составления статистического уравнения однофакторной зависимости и дальнейшего анализа этой зависимости. Для этого рассмотрим три модели:
прямая однофакторная линейная связь при одновременном увеличении факторного и результативного признаков;
логарифмическая модель (прямая гипербола, когда уровень результативного признака возрастает, а затем его рост приостанавливается, оставаясь почти на одном уровне);
прямая логическая зависимость (когда происходит неустойчивое возрастание уровня результативного признака).
Линейная модель.
Уравнение модели прямой однофакторной линейной связи:
![]()
Для вычисления параметра ![]() , составления уравнения однофакторной зависимости и дальнейшего анализа этой зависимости заполним таблицу 4.2.
, составления уравнения однофакторной зависимости и дальнейшего анализа этой зависимости заполним таблицу 4.2.
Таблица 4.2
|
|
|
|
|
|
|
| 1,0 | 466 | 0,0 | 0,000 | 0,000 | 466,000 |
| 1,0 | 549 | 0,0 | 0,178 | 0,000 | 466,000 |
| 1,0 | 978 | 0,0 | 1,099 | 0,000 | 466,000 |
| 4,0 | 495 | 3,0 | 0,062 | 0,685 | 785,222 |
| 4,0 | 723 | 3,0 | 0,552 | 0,685 | 785,222 |
| 4,0 | 681 | 3,0 | 0,461 | 0,685 | 785,222 |
| 4,5 | 619 | 3,5 | 0,328 | 0,799 | 838,426 |
| 4,5 | 1049 | 3,5 | 1,251 | 0,799 | 838,426 |
| 4,5 | 1033 | 3,5 | 1,217 | 0,799 | 838,426 |
| 5,0 | 163 | 4,0 | -0,650 | 0,913 | 891,630 |
| 5,0 | 182 | 4,0 | -0,609 | 0,913 | 891,630 |
| 5,0 | 890 | 4,0 | 0,910 | 0,913 | 891,630 |
| 5,0 | 1522 | 4,0 | 2,266 | 0,913 | 891,630 |
| 5,0 | 1194 | 4,0 | 1,562 | 0,913 | 891,630 |
| 5,5 | 987 | 4,5 | 1,118 | 1,028 | 944,833 |
| 6,0 | 764 | 5,0 | 0,639 | 1,142 | 998,037 |
| 6,0 | 1373 | 5,0 | 1,946 | 1,142 | 998,037 |
|
| 54,0 | 12,330 | |||
Примечание. Предпоследний и последний столбцы таблицы 4.2 заполняются после отыскания параметра уравнения зависимости ![]() и составления самого уравнения зависимости.
и составления самого уравнения зависимости.
В рассматриваемом примере параметр ![]() , при
, при ![]() и
и ![]() вычисляется по формуле:
вычисляется по формуле:
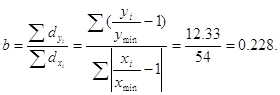
В рассматриваемом примере окончательный вид уравнения зависимости находим по формуле.:
![]()
Отобразим эмпирические и теоретические значения результативного признака на графике (рисунок 4).
Рисунок 4

Информация для расчета коэффициента детерминации в типовой задаче в полном объеме представлена в таблице 4.3.
Таблица 4.3
|
|
|
|
|
|
| ( |
|
| 1,0 | 466 | 0,000 | 466,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 1,0 | 549 | 0,178 | 466,000 | 0,032 | 0,000 | 0,178 | 0,032 |
| 1,0 | 978 | 1,099 | 466,000 | 1,207 | 0,000 | 1,099 | 1,207 |
| 4,0 | 495 | 0,062 | 785,222 | 0,004 | 0,685 | -0,623 | 0,388 |
| 4,0 | 723 | 0,552 | 785,222 | 0,304 | 0,685 | -0,134 | 0,018 |
| 4,0 | 681 | 0,461 | 785,222 | 0,213 | 0,685 | -0,224 | 0,050 |
| 4,5 | 619 | 0,328 | 838,426 | 0,108 | 0,799 | -0,471 | 0,222 |
| 4,5 | 1049 | 1,251 | 838,426 | 1,565 | 0,799 | 0,452 | 0,204 |
| 4,5 | 1033 | 1,217 | 838,426 | 1,480 | 0,799 | 0,418 | 0,174 |
| 5,0 | 163 | -0,650 | 891,630 | 0,423 | 0,913 | -1,564 | 2,445 |
| 5,0 | 182 | -0,609 | 891,630 | 0,371 | 0,913 | -1,523 | 2,319 |
| 5,0 | 890 | 0,910 | 891,630 | 0,828 | 0,913 | -0,003 | 0,000 |
| 5,0 | 1522 | 2,266 | 891,630 | 5,135 | 0,913 | 1,353 | 1,830 |
| 5,0 | 1194 | 1,562 | 891,630 | 2,441 | 0,913 | 0,649 | 0,421 |
| 5,5 | 987 | 1,118 | 944,833 | 1,250 | 1,028 | 0,090 | 0,008 |
| 6,0 | 764 | 0,639 | 998,037 | 0,409 | 1,142 | -0,502 | 0,252 |
| 6,0 | 1373 | 1,946 | 998,037 | 3,788 | 1,142 | 0,805 | 0,647 |
|
| 12,330 | 19,558 | 10,217 | ||||
По данным таблицы 4.3 коэффициент детерминации составит:
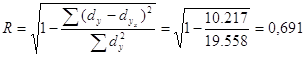
Логарифмическая модель
Уравнение модели прямой гиперболы:
![]()
Для вычисления параметра ![]() , составления уравнения однофакторной зависимости и дальнейшего анализа этой зависимости заполним таблицу 4.4.
, составления уравнения однофакторной зависимости и дальнейшего анализа этой зависимости заполним таблицу 4.4.
Таблица 4.4
|
|
|
|
|
|
|
| 1,0 | 466 | 0,000 | 0,000 | 0,000 | 466,000 |
| 1,0 | 549 | 0,000 | 0,178 | 0,000 | 466,000 |
| 1,0 | 978 | 0,000 | 1,099 | 0,000 | 466,000 |
| 4,0 | 495 | 0,750 | 0,062 | 1,006 | 934,912 |
| 4,0 | 723 | 0,750 | 0,552 | 1,006 | 934,912 |
| 4,0 | 681 | 0,750 | 0,461 | 1,006 | 934,912 |
| 4,5 | 619 | 0,778 | 0,328 | 1,044 | 952,279 |
| 4,5 | 1049 | 0,778 | 1,251 | 1,044 | 952,279 |
| 4,5 | 1033 | 0,778 | 1,217 | 1,044 | 952,279 |
| 5,0 | 163 | 0,800 | 0,650 | 1,073 | 966,172 |
| 5,0 | 182 | 0,800 | 0,609 | 1,073 | 966,172 |
| 5,0 | 890 | 0,800 | 0,910 | 1,073 | 966,172 |
| 5,0 | 1522 | 0,800 | 2,266 | 1,073 | 966,172 |
| 5,0 | 1194 | 0,800 | 1,562 | 1,073 | 966,172 |
| 5,5 | 987 | 0,818 | 1,118 | 1,098 | 977,540 |
| 6,0 | 764 | 0,833 | 0,639 | 1,118 | 987,013 |
| 6,0 | 1373 | 0,833 | 1,946 | 1,118 | 987,013 |
|
| 11,068 | 14,850 | 14,850 | ||
Примечание. Предпоследний и последний столбцы таблицы 4.4 заполняются после отыскания параметра уравнения зависимости ![]() и составления самого уравнения зависимости.
и составления самого уравнения зависимости.
В рассматриваемом примере параметр ![]() , при
, при ![]() и
и ![]() вычисляется по формуле:
вычисляется по формуле:
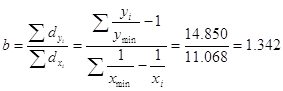
В рассматриваемом примере окончательный вид уравнения зависимости находим по формуле:
![]()
Отобразим эмпирические и теоретические значения результативного признака на графике (рисунок 5).
Рисунок 5
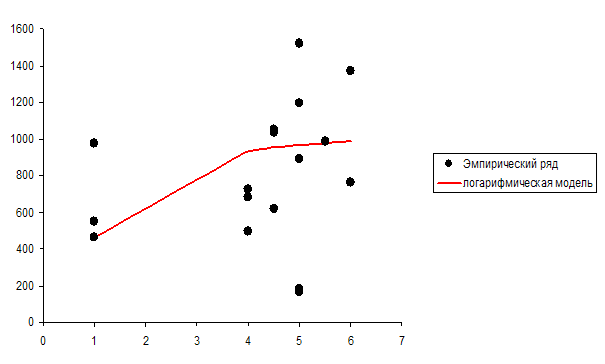
Информация для расчета коэффициента детерминации в типовой задаче в полном объеме представлена в таблице 4.5.
Таблица 4.5
|
|
|
|
|
|
| ( |
|
| 1,0 | 466 | 0,000 | 466,000 | 0,000 | 0,000 | 0,000 | 0,00000 |
| 1,0 | 549 | 0,178 | 466,000 | 0,032 | 0,000 | 0,178 | 0,03172 |
| 1,0 | 978 | 1,099 | 466,000 | 1,207 | 0,000 | 1,099 | 1,20717 |
| 4,0 | 495 | 0,062 | 934,912 | 0,004 | 1,006 | -0,944 | 0,89117 |
| 4,0 | 723 | 0,552 | 934,912 | 0,304 | 1,006 | -0,455 | 0,20679 |
| 4,0 | 681 | 0,461 | 934,912 | 0,213 | 1,006 | -0,545 | 0,29689 |
| 4,5 | 619 | 0,328 | 952,279 | 0,108 | 1,044 | -0,715 | 0,51150 |
| 4,5 | 1049 | 1,251 | 952,279 | 1,565 | 1,044 | 0,208 | 0,04308 |
| 4,5 | 1033 | 1,217 | 952,279 | 1,480 | 1,044 | 0,173 | 0,03001 |
| 5,0 | 163 | 0,650 | 966,172 | 0,423 | 1,073 | -0,423 | 0,17903 |
| 5,0 | 182 | 0,609 | 966,172 | 0,371 | 1,073 | -0,464 | 0,21519 |
| 5,0 | 890 | 0,910 | 966,172 | 0,828 | 1,073 | -0,163 | 0,02672 |
| 5,0 | 1522 | 2,266 | 966,172 | 5,135 | 1,073 | 1,193 | 1,42268 |
| 5,0 | 1194 | 1,562 | 966,172 | 2,441 | 1,073 | 0,489 | 0,23902 |
| 5,5 | 987 | 1,118 | 977,540 | 1,250 | 1,098 | 0,020 | 0,00041 |
| 6,0 | 764 | 0,639 | 987,013 | 0,409 | 1,118 | -0,479 | 0,22903 |
| 6,0 | 1373 | 1,946 | 987,013 | 3,788 | 1,118 | 0,828 | 0,68608 |
|
| 14,850 | 19,558 | 6,21649 | ||||
По данным таблицы 4.5 коэффициент детерминации составит:
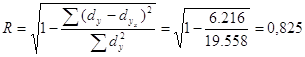
Логическая модель
Уравнение модели прямой логической зависимости:
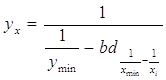
Для вычисления параметра ![]() , составления уравнения однофакторной зависимости и дальнейшего анализа этой зависимости заполним таблицу 5.
, составления уравнения однофакторной зависимости и дальнейшего анализа этой зависимости заполним таблицу 5.
Таблица 4.6
|
|
|
|
|
|
|
|
|
| 1,0 | 466 | 1,00000 | 0,00215 | 0,00000 | 0,00000 | 0,00000 | 466,00000 |
| 1,0 | 549 | 1,00000 | 0,00182 | 0,00000 | 0,00032 | 0,00000 | 466,00000 |
| 1,0 | 978 | 1,00000 | 0,00102 | 0,00000 | 0,00112 | 0,00000 | 466,00000 |
| 4,0 | 495 | 0,25000 | 0,00202 | 0,75000 | 0,00013 | 0,00039 | 570,13230 |
| 4,0 | 723 | 0,25000 | 0,00138 | 0,75000 | 0,00076 | 0,00039 | 570,13230 |
| 4,0 | 681 | 0,25000 | 0,00147 | 0,75000 | 0,00068 | 0,00039 | 570,13230 |
| 4,5 | 619 | 0,22222 | 0,00162 | 0,77778 | 0,00053 | 0,00041 | 574,89026 |
| 4,5 | 1049 | 0,22222 | 0,00095 | 0,77778 | 0,00119 | 0,00041 | 574,89026 |
| 4,5 | 1033 | 0,22222 | 0,00097 | 0,77778 | 0,00118 | 0,00041 | 574,89026 |
| 5,0 | 163 | 0,20000 | 0,00613 | 0,80000 | -0,00399 | 0,00042 | 578,75418 |
| 5,0 | 182 | 0,20000 | 0,00549 | 0,80000 | -0,00335 | 0,00042 | 578,75418 |
| 5,0 | 890 | 0,20000 | 0,00112 | 0,80000 | 0,00102 | 0,00042 | 578,75418 |
| 5,0 | 1522 | 0,20000 | 0,00066 | 0,80000 | 0,00149 | 0,00042 | 578,75418 |
| 5,0 | 1194 | 0,20000 | 0,00084 | 0,80000 | 0,00131 | 0,00042 | 578,75418 |
| 5,5 | 987 | 0,18182 | 0,00101 | 0,81818 | 0,00113 | 0,00043 | 581,95443 |
| 6,0 | 764 | 0,16667 | 0,00131 | 0,83333 | 0,00084 | 0,00044 | 584,64846 |
| 6,0 | 1373 | 0,16667 | 0,00073 | 0,83333 | 0,00142 | 0,00044 | 584,64846 |
|
| 11,06818 | 0,00578 | |||||
Примечание. Предпоследний и последний столбцы таблицы 4.6 заполняются после отыскания параметра уравнения зависимости ![]() и составления самого уравнения зависимости.
и составления самого уравнения зависимости.
В рассматриваемом примере параметр ![]() , при
, при ![]() и
и ![]() вычисляется по формуле:
вычисляется по формуле:
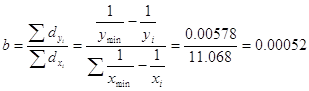
В рассматриваемом примере окончательный вид уравнения зависимости находим по формуле:
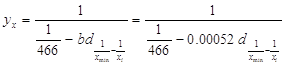
Отобразим эмпирические и теоретические значения результативного признака на графике (рисунок 6).
Рисунок 6
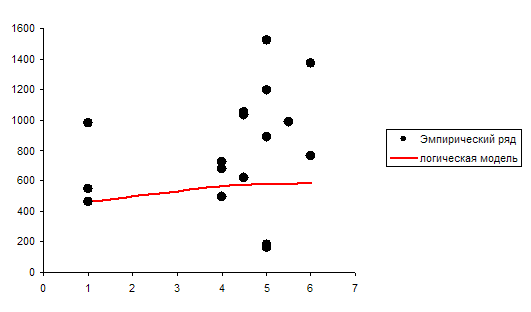
Информация для расчета коэффициента детерминации в типовой задаче в полном объеме представлена в таблице 4.7.
Таблица 4.7
|
|
|
|
|
|
| ( |
|
| 1,0 | 466 | 0,000 | 466,00 | 0,0000000 | 0,0000000 | 0,0000000 | 0,0000000 |
| 1,0 | 549 | 0,000 | 466,00 | 0,0000001 | 0,0000000 | 0,0003244 | 0,0000001 |
| 1,0 | 978 | 0,001 | 466,00 | 0,0000013 | 0,0000000 | 0,0011234 | 0,0000013 |
| 4,0 | 495 | 0,000 | 570,13 | 0,0000000 | 0,0003919 | -0,0002662 | 0,0000001 |
| 4,0 | 723 | 0,001 | 570,13 | 0,0000006 | 0,0003919 | 0,0003709 | 0,0000001 |
| 4,0 | 681 | 0,001 | 570,13 | 0,0000005 | 0,0003919 | 0,0002856 | 0,0000001 |
| 4,5 | 619 | 0,001 | 574,89 | 0,0000003 | 0,0004065 | 0,0001240 | 0,0000000 |
| 4,5 | 1049 | 0,001 | 574,89 | 0,0000014 | 0,0004065 | 0,0007862 | 0,0000006 |
| 4,5 | 1033 | 0,001 | 574,89 | 0,0000014 | 0,0004065 | 0,0007714 | 0,0000006 |
| 5,0 | 163 | -0,004 | 578,75 | 0,0000159 | 0,0004181 | -0,0044071 | 0,0000194 |
| 5,0 | 182 | -0,003 | 578,75 | 0,0000112 | 0,0004181 | -0,0037667 | 0,0000142 |
| 5,0 | 890 | 0,001 | 578,75 | 0,0000010 | 0,0004181 | 0,0006043 | 0,0000004 |
| 5,0 | 1522 | 0,001 | 578,75 | 0,0000022 | 0,0004181 | 0,0010708 | 0,0000011 |
| 5,0 | 1194 | 0,001 | 578,75 | 0,0000017 | 0,0004181 | 0,0008903 | 0,0000008 |
| 5,5 | 987 | 0,001 | 581,95 | 0,0000013 | 0,0004276 | 0,0007052 | 0,0000005 |
| 6,0 | 764 | 0,001 | 584,65 | 0,0000007 | 0,0004355 | 0,0004015 | 0,0000002 |
| 6,0 | 1373 | 0,001 | 584,65 | 0,0000020 | 0,0004355 | 0,0009821 | 0,0000010 |
|
| 0,006 | 0,0000416 | 0,0000404 | ||||
По данным таблицы 4.7 коэффициент детерминации составит:
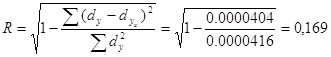
Сравним коэффициенты детерминации по трем моделям
Таблица 4.8
| Тип трендовой модели | Уравнения зависимостей |
|
| Линейная |
| 0,477 |
| Логарифмическая |
| 0,682 |
| Логическая |
| 0,028 |
![]() Чем слабее линейная связь между X и Y, тем R2 ближе к нулю, и чем эта связь значительнее, тем ближе R2 к единице.
Чем слабее линейная связь между X и Y, тем R2 ближе к нулю, и чем эта связь значительнее, тем ближе R2 к единице.
Вывод: Анализируя результаты представленные в таблице 4.8 можно прийти к выводу что из представленных трендовых моделей, логарифмическая модель является наиболее адекватной.
Похожие работы
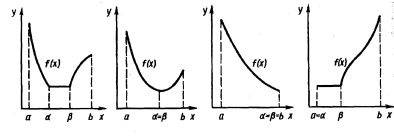
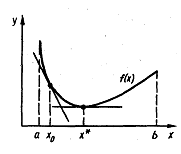
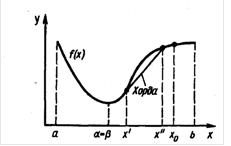
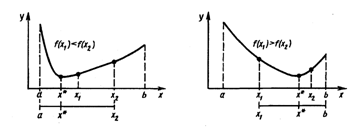
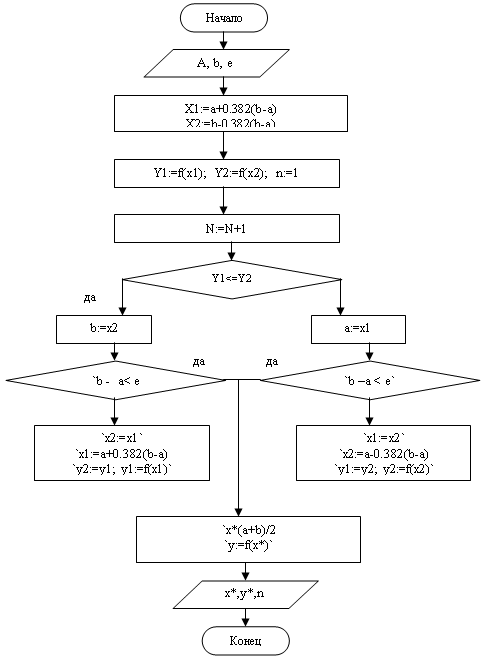
... 4 - график унимодальной, но не выпуклой функции Таким образом, кроме перечисленных свойств, выпуклые функции обладают также и всеми свойствами унимодальных функций. 2. Прямые методы безусловной оптимизации Для решения задачи минимизации функции f (х) на отрезке [а; b] на практике, как правило, применяют приближенные методы. Они позволяют найти решение этой задачи с необходимой точностью ...
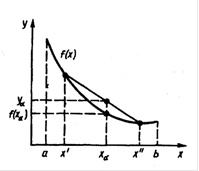
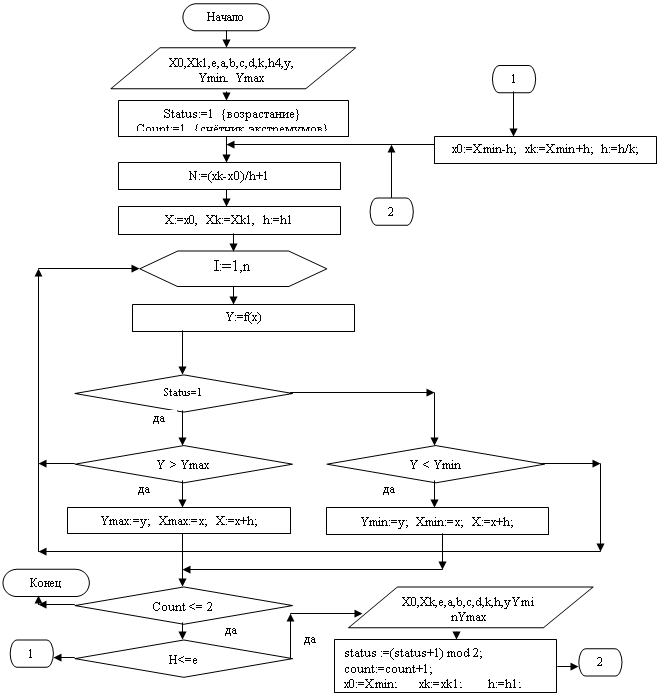
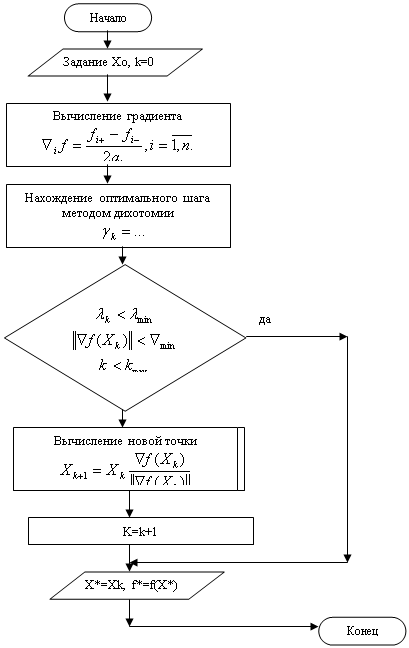
... : т.е. . Для определения координат точки Х1 нужно выбрать значение шага . Получим : Из соотношения (,)=0 имеем: (-3-3)(-3)+(1+)=10+10=0 откуда = Задание 4 ПРИМЕНЕНИЕ ГРАДИЕНТНЫХ МЕТОДОВ ДЛЯ ОПТИМИЗАЦИИ НА ЭВМ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ОБЪЕКТОВ Цель задания: приобрести практические навыки разработки алгоритмов и программ оптимизации математических моделей градиентным методом. ...
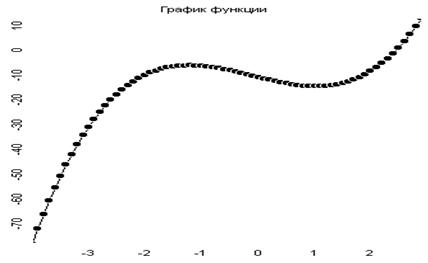
... от года-x и от номера месяца в году-y следующим образом: F(x)=50-x2+10x-y2+10y. Определите, в каком году и в каком месяце прибыль была максимальной. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МЕТОДЫ ОПТИМИЗАЦИИ Билет № 22 1) Постановка вариационной задачи с ограничениями. Привести пример. 2) Дайте геометрическую ...
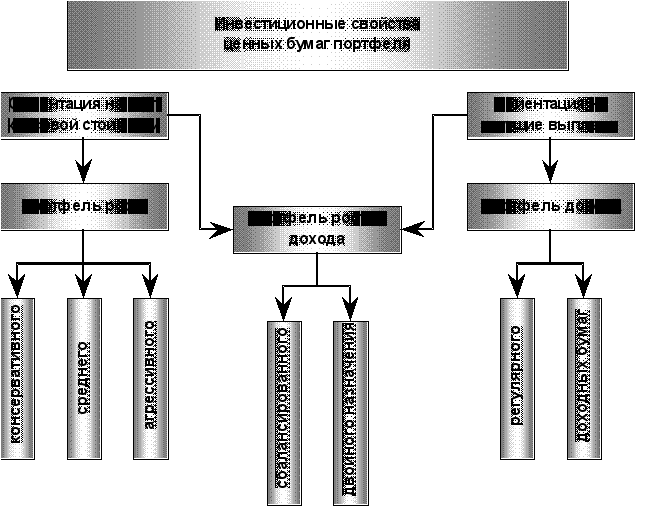
... , портфель ценных бумаг является тем инструментом, с помощью которого инвестору обеспечивается требуемая устойчивость дохода при минимальном риске. 3. ПРИНЦИПЫ ФОРМИРОВАНИЯ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ При формировании инвестиционного портфеля следует руководствоваться следующими соображениями: безопасность вложений (неуязвимость инвестиций от потрясений на рынке инвестиционного капитала), ...
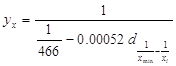

0 комментариев