Навигация
Задача выбора оптимального пути в транспортной сети
2 Задача выбора оптимального пути в транспортной сети
Задача: В предложенной транспортной сети (см. рисунок 1) имеется несколько маршрутов по проезду из начального пункта (1) в конечный пункт (11). Стоимость проезда между отдельными пунктами транспортной сети представлена в таблице 2.1. Необходимо определить оптимальный маршрут проезда из пункта 1 в пункт 11 с минимальными транспортными расходами.
Рисунок 1
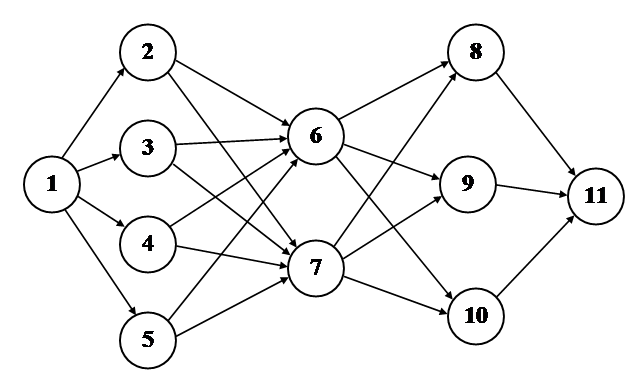
Таблица 2.1
| Начальный путь | Конечный путь | T(i,j) |
| 1 | 2 | 5 |
| 1 | 3 | 7 |
| 1 | 4 | 6 |
| 1 | 5 | 10 |
| 2 | 6 | 3 |
| 2 | 7 | 7 |
| 3 | 6 | 8 |
| 3 | 7 | 9 |
| 4 | 6 | 11 |
| 4 | 7 | 4 |
| 5 | 6 | 8 |
| 5 | 7 | 9 |
| 6 | 8 | 4 |
| 6 | 9 | 5 |
| 6 | 10 | 4 |
| 7 | 8 | 5 |
| 7 | 9 | 12 |
| 7 | 10 | 6 |
| 8 | 11 | 10 |
| 9 | 11 | 8 |
| 10 | 11 | 10 |
В данной задаче имеется ограничение – двигаться по магистралям можно только слева направо. Это дает нам возможность разбить всю транспортную сеть на пояса и отнести каждый из десяти пунктов к одному из четырех поясов. Будем говорить, что пункт принадлежит k-му поясу, если из него можно попасть в конечный пункт ровно за k шагов, т.е. заездом ровно в k-1 промежуточный пункт. Таким образом, пункты 8, 9 и 10 принадлежат к первому поясу; 6 и 7 – ко второму; 2, 3, 4 и 5 – к третьему; 1 – к четвертому. На k-м шаге будем находить оптимальные маршруты из городов k-го пояса до конечного пункта.
Оптимизацию будем производить с хвоста процесса, и потому, добравшись до k-го шага, мы не можем знать, в какой именно из городов k-го пояса мы попадем, двигаясь из пункта 1. Поэтому для каждого из этих городов мы должны будем найти оптимальный маршрут до конечного пункта. Очевидно, что минимально возможная стоимость проезда до пункта 11 будет зависеть только от того, в каком из городов этого пояса мы оказались. Номер S города, принадлежащего k-му поясу, и будет называться переменной состояния данной системы на k-м шаге. Нужно помнить, что, добравшись до k-го шага, мы уже осуществили предыдущие шаги, в частности, нашли оптимальные маршруты по перемещению из любого города (k-1)-го пояса в конечный пункт. Таким образом, находясь в некотором городе S k-го пояса, мы должны принять решение о том, в какой из городов (k-1)-го пояса следует отправиться, а направление дальнейшего движения уже известно нам из предыдущих шагов. Номер J города (k-1)-го пояса будет являться переменной управления на k-м шаге.
Функция Беллмана на k-м шаге решения задачи дает нам возможность рассчитать минимальную стоимость проезда из города S (k-го пояса) до конечного пункта. Для первого шага (k=1) эту величину отыскать не сложно – это стоимость проезда из городов 1-го пояса непосредственно до конечного пункта: F1(i)=Ci11. Для последующих же шагов стоимость проезда складывается из двух слагаемых – стоимости проезда из города S k-го пояса в город J (k-1)-го пояса и минимально возможной стоимости проезда из города J до конечного пункта, т.е. Fk-1(J).
Таким образом, функциональное уравнение Беллмана на k-м шаге решения будет иметь вид:
![]()
Минимум стоимости достигается на некотором значении J*, которое и является оптимальным направлением движения из пункта S в сторону конечного пункта.
Решение:
Этап I. Условная оптимизация.
Шаг 1. k = 1. F1(S) = ts11.
Таблица 2.2
| S | J = 11 | F1(S) | J* |
| 8 | 10 | 10 | 11 |
| 9 | 8 | 8 | 11 |
| 10 | 10 | 10 | 11 |
Шаг 2. k = 2. Функциональное уравнение на данном шаге принимает вид:
![]() .
.
Результаты расчета по приведенной формуле приведены в таблице 2.3:
Таблица 2.3
| S | J = 8 | J = 9 | J = 10 | F2(S) | J* |
| 6 | 4 + 10 | 5 + 8 | 4 + 10 | 13 | 9 |
| 7 | 5 + 10 | 12 + 8 | 6 + 10 | 15 | 8 |
Шаг 3. k = 3. Функциональное уравнение на данном шаге принимает вид:
![]() .
.
Результаты расчета по приведенной формуле приведены в таблице 2.4:
Таблица 2.4
| S | J = 6 | J = 7 | F3(S) | J* |
| 2 | 3 + 13 | 7 + 15 | 16 | 6 |
| 3 | 8 + 13 | 9 + 15 | 21 | 6/7 |
| 4 | 11 + 13 | 4 + 15 | 19 | 7 |
| 5 | 8 + 13 | 9 + 15 | 21 | 6/7 |
Шаг 4. k = 4. Функциональное уравнение на данном шаге принимает вид:
![]() .
.
Результаты расчета по приведенной формуле приведены в таблице 2.5:
Таблица 2.5
| S | J = 2 | J = 3 | J = 4 | J = 5 | F4(S) | J* |
| 1 | 5 + 16 | 7 + 21 | 6 + 19 | 10 + 21 | 21 | 2 |
Этап II. Безусловная оптимизация.
На этапе условной оптимизации получено, что минимальные затраты на проезд из пункта 1 в пункт 11 составляют F4(1) = 21, что достигается следующим движением по магистралям. Из пункта 1 следует направиться в пункт 2, затем из него в пункт 6, затем в пункт 9 и из него в пункт 11.
Ответ: Оптимальным маршрутом из пункта 1 в пункт 11 является маршрут 1 – 2 – 6 – 9 – 11.
Похожие работы
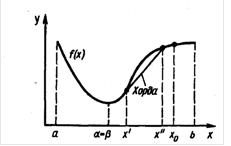
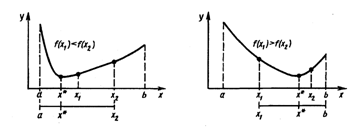
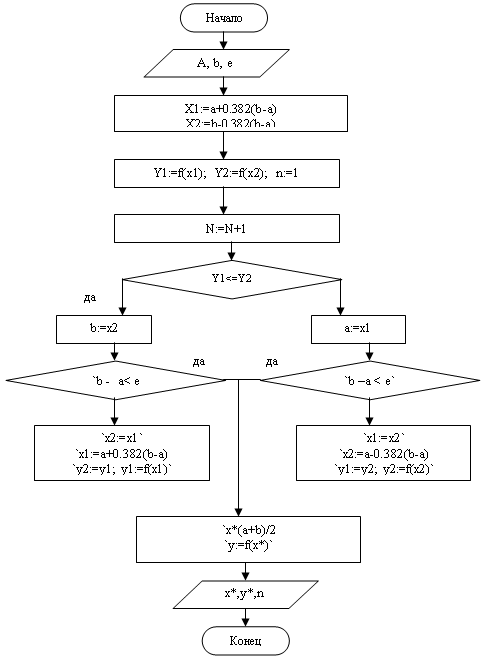
... 4 - график унимодальной, но не выпуклой функции Таким образом, кроме перечисленных свойств, выпуклые функции обладают также и всеми свойствами унимодальных функций. 2. Прямые методы безусловной оптимизации Для решения задачи минимизации функции f (х) на отрезке [а; b] на практике, как правило, применяют приближенные методы. Они позволяют найти решение этой задачи с необходимой точностью ...
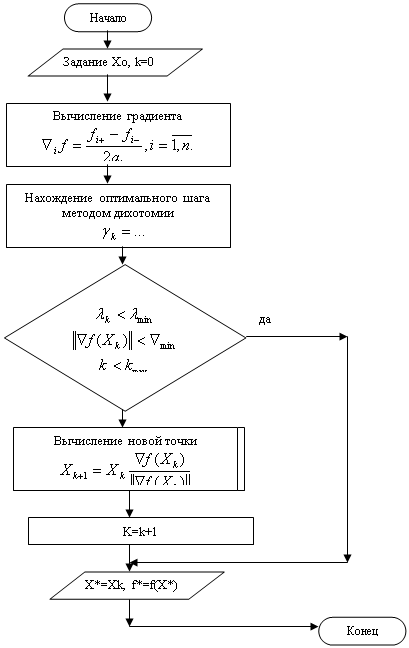
... : т.е. . Для определения координат точки Х1 нужно выбрать значение шага . Получим : Из соотношения (,)=0 имеем: (-3-3)(-3)+(1+)=10+10=0 откуда = Задание 4 ПРИМЕНЕНИЕ ГРАДИЕНТНЫХ МЕТОДОВ ДЛЯ ОПТИМИЗАЦИИ НА ЭВМ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ОБЪЕКТОВ Цель задания: приобрести практические навыки разработки алгоритмов и программ оптимизации математических моделей градиентным методом. ...
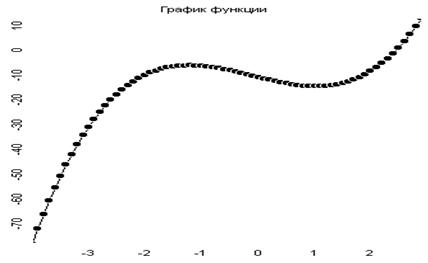
... от года-x и от номера месяца в году-y следующим образом: F(x)=50-x2+10x-y2+10y. Определите, в каком году и в каком месяце прибыль была максимальной. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МЕТОДЫ ОПТИМИЗАЦИИ Билет № 22 1) Постановка вариационной задачи с ограничениями. Привести пример. 2) Дайте геометрическую ...
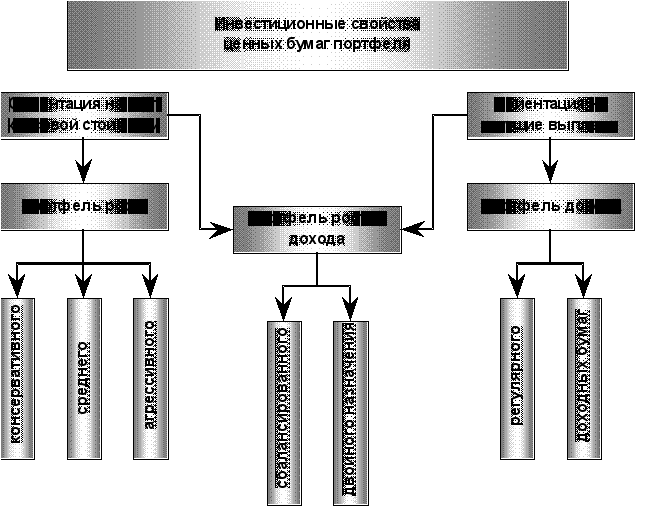
... , портфель ценных бумаг является тем инструментом, с помощью которого инвестору обеспечивается требуемая устойчивость дохода при минимальном риске. 3. ПРИНЦИПЫ ФОРМИРОВАНИЯ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ При формировании инвестиционного портфеля следует руководствоваться следующими соображениями: безопасность вложений (неуязвимость инвестиций от потрясений на рынке инвестиционного капитала), ...

0 комментариев