Задача выбора оптимального пути в транспортной сети
Методы Хэмминга и Брауна
Метод Хемминга
Метод Брауна
Идентификация как функция управления
Провести процедуру структурно-параметрической идентификации математической модели для исходных данных. Оценить адекватность
Стимулирование и мотивация как функции управления
Задача стимулирования для многоэлементной системы с сильносвязанными агентами
Навигация
Задача стимулирования для многоэлементной системы с сильносвязанными агентами
Методы безусловной многомерной оптимизации
28886
знаков
51
таблица
16
изображений
3. Задача стимулирования для многоэлементной системы с сильносвязанными агентами.
Руководитель (центр) поручает работу бригаде, состоящей из 2 рабочих. Рабочие (агенты) изготавливают однородную продукцию объёмом yi , которую центр продаёт по цене p=1500. Центр использует пропорциональную систему стимулирования
,
где 
– ставка оплаты единицы продукции.
Затраты агентов определяются соответственно:
,
.
Фонд заработной платы, которым располагает центр составляет R=37000 денежных единиц. Определить параметры системы стимулирования .
Решение
Запишем целевую функцию центра:
 |
(3.3.1)
и целевые функции агентов:
 |
(3.3.2)
(3.3.3)
Сформулируем задачу стимулирования:
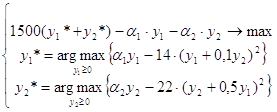(3.3.4)
(3.3.5)
(3.3.6)
Первый этап. Найдем реакцию первого агента из решения оптимизационной задачи. Для этого продифференцируем целевую функцию агента по 
и приравняем к нулю:
 |
Решая уравнение, определим реакцию первого агента:
 |
Аналогично найдём реакцию второго агента:
 | ||
 | ||
Решив систему уравнений:
 |
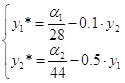относительно y1 и y2получим реакции агентов:
 | ||
 | ||
Второй этап. Подставим реакции агентов в целевую функцию центра:
 |
Продифференцировав это выражение по 
,
и приравняв нулю, получим систему уравнений:
 |
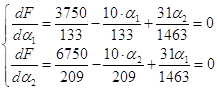Решив полученную систему уравнений, определим параметры системы
стимулирования и
Ответ: параметры системы стимулирования 
и 
равны 645,83 и 961,01 соответственно.
Похожие работы
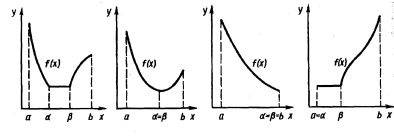
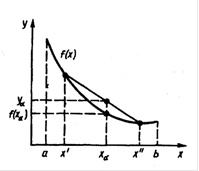
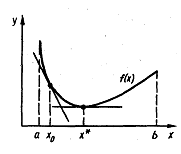
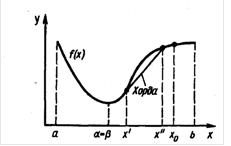
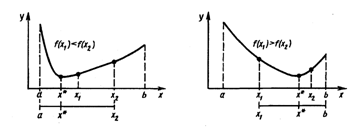
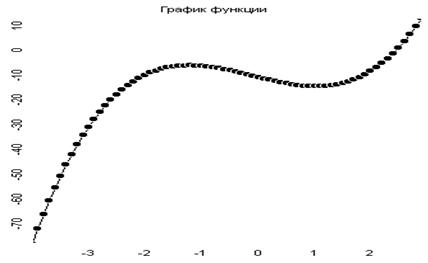
... 4 - график унимодальной, но не выпуклой функции Таким образом, кроме перечисленных свойств, выпуклые функции обладают также и всеми свойствами унимодальных функций. 2. Прямые методы безусловной оптимизации Для решения задачи минимизации функции f (х) на отрезке [а; b] на практике, как правило, применяют приближенные методы. Они позволяют найти решение этой задачи с необходимой точностью ...
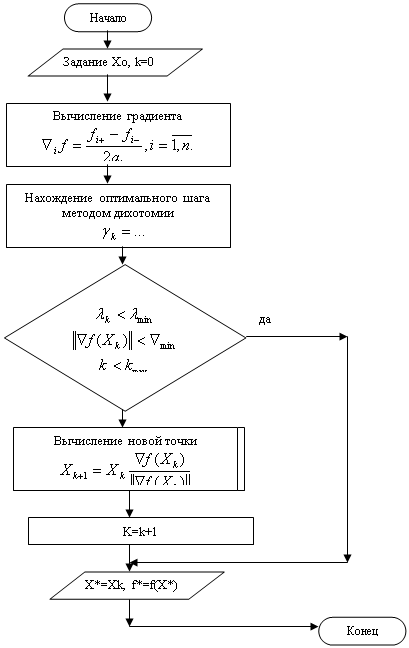
... : т.е. . Для определения координат точки Х1 нужно выбрать значение шага . Получим : Из соотношения (,)=0 имеем: (-3-3)(-3)+(1+)=10+10=0 откуда = Задание 4 ПРИМЕНЕНИЕ ГРАДИЕНТНЫХ МЕТОДОВ ДЛЯ ОПТИМИЗАЦИИ НА ЭВМ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ОБЪЕКТОВ Цель задания: приобрести практические навыки разработки алгоритмов и программ оптимизации математических моделей градиентным методом. ...
... от года-x и от номера месяца в году-y следующим образом: F(x)=50-x2+10x-y2+10y. Определите, в каком году и в каком месяце прибыль была максимальной. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МЕТОДЫ ОПТИМИЗАЦИИ Билет № 22 1) Постановка вариационной задачи с ограничениями. Привести пример. 2) Дайте геометрическую ...
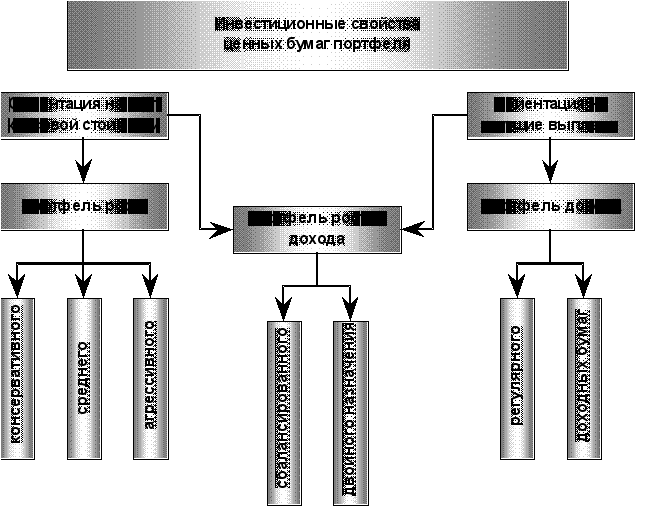
... , портфель ценных бумаг является тем инструментом, с помощью которого инвестору обеспечивается требуемая устойчивость дохода при минимальном риске. 3. ПРИНЦИПЫ ФОРМИРОВАНИЯ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ При формировании инвестиционного портфеля следует руководствоваться следующими соображениями: безопасность вложений (неуязвимость инвестиций от потрясений на рынке инвестиционного капитала), ...
0 комментариев